Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 20.9 Профильный Уровень Мордкович — Подробные Ответы
Постройте график функции:
а) ;
б) ;
в) ;
г)
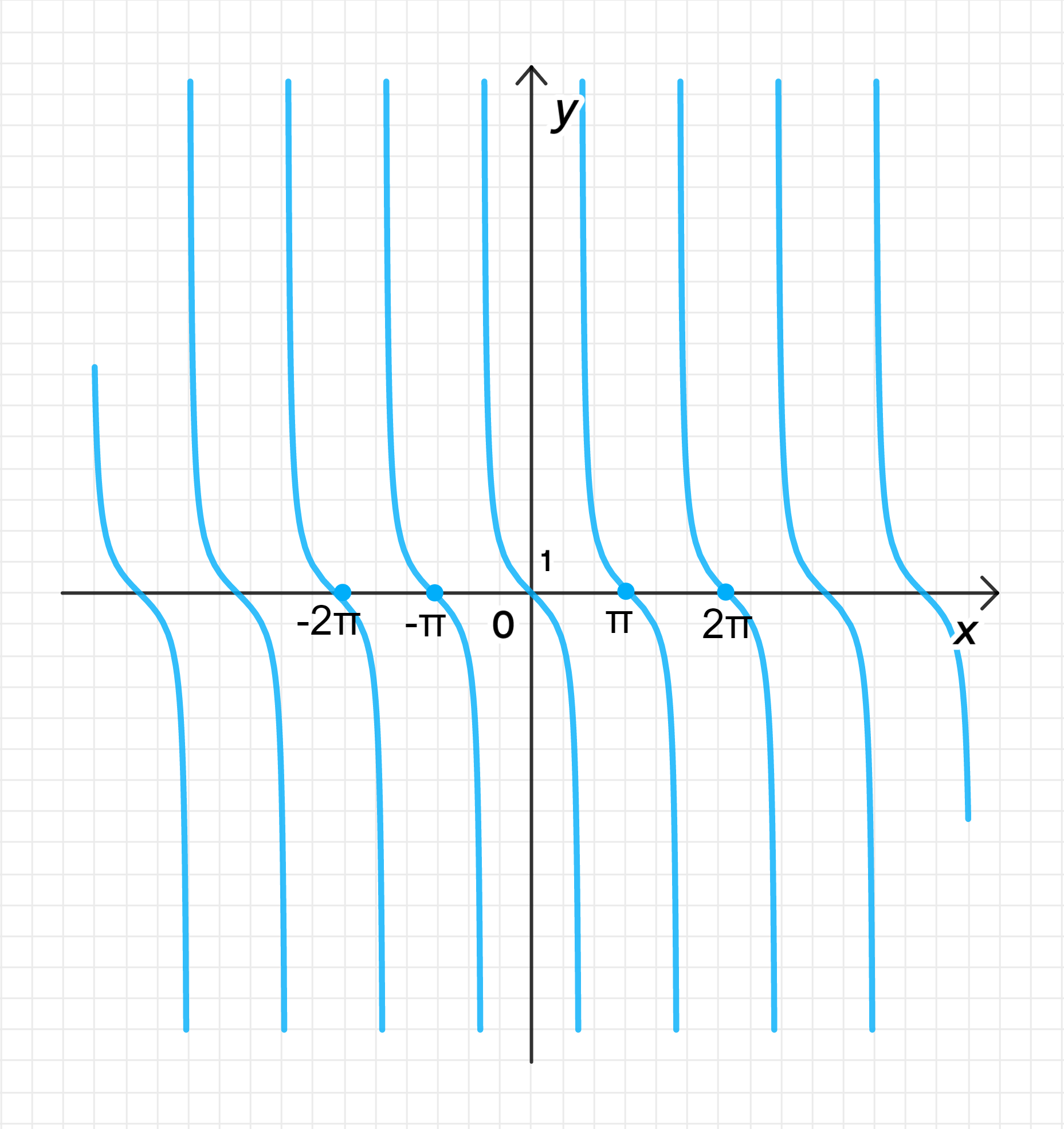
а) ;
Главная ветвь тангенсоиды имеет центр в точке ;
Ветвь лежит на интервале: ;
Ветвь отражена относительно прямой ;
График функции:
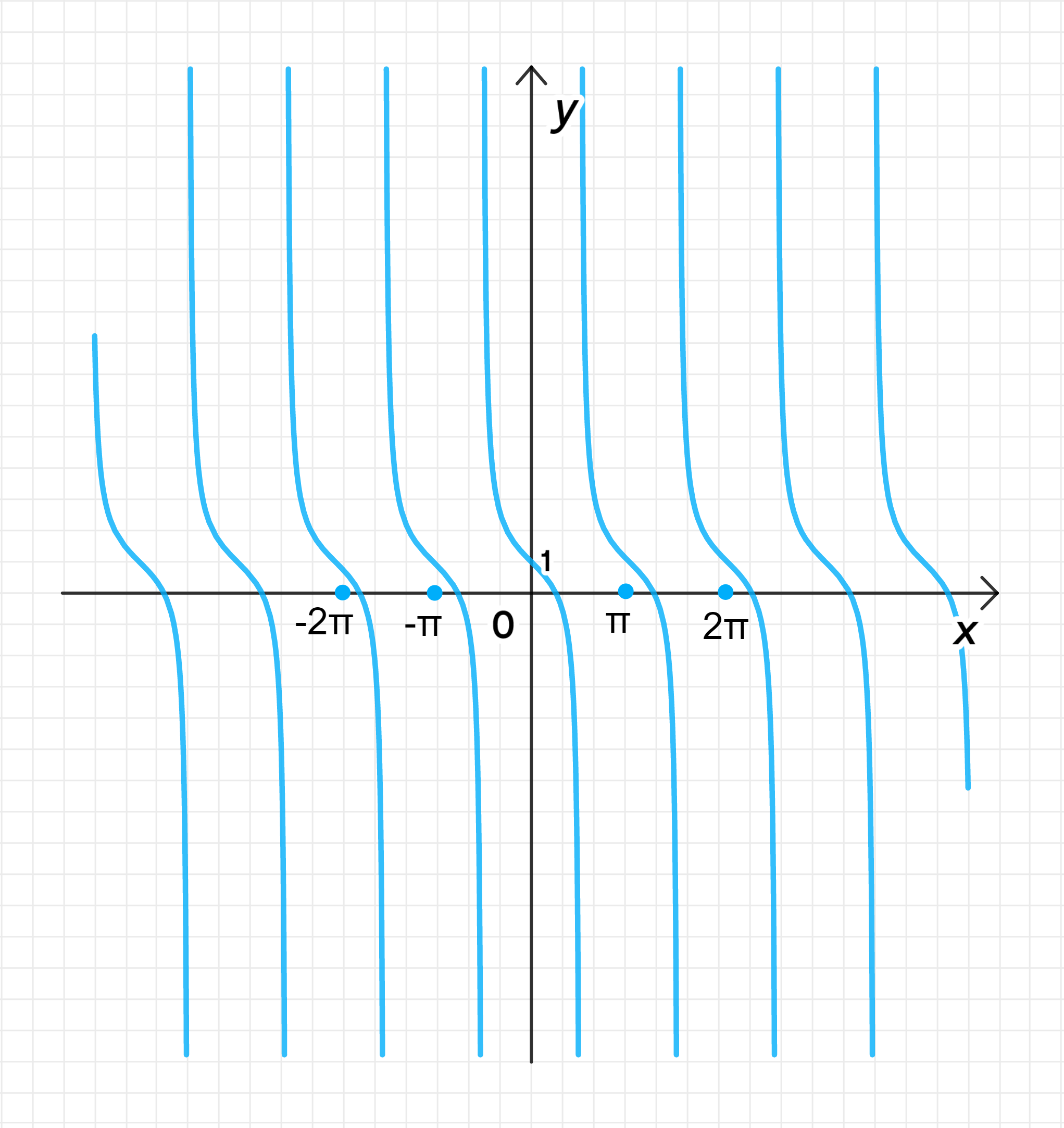
б) ;
Главная ветвь тангенсоиды имеет центр в точке ;
Ветвь лежит на интервале: ;
Ветвь отражена относительно прямой ;
График функции:
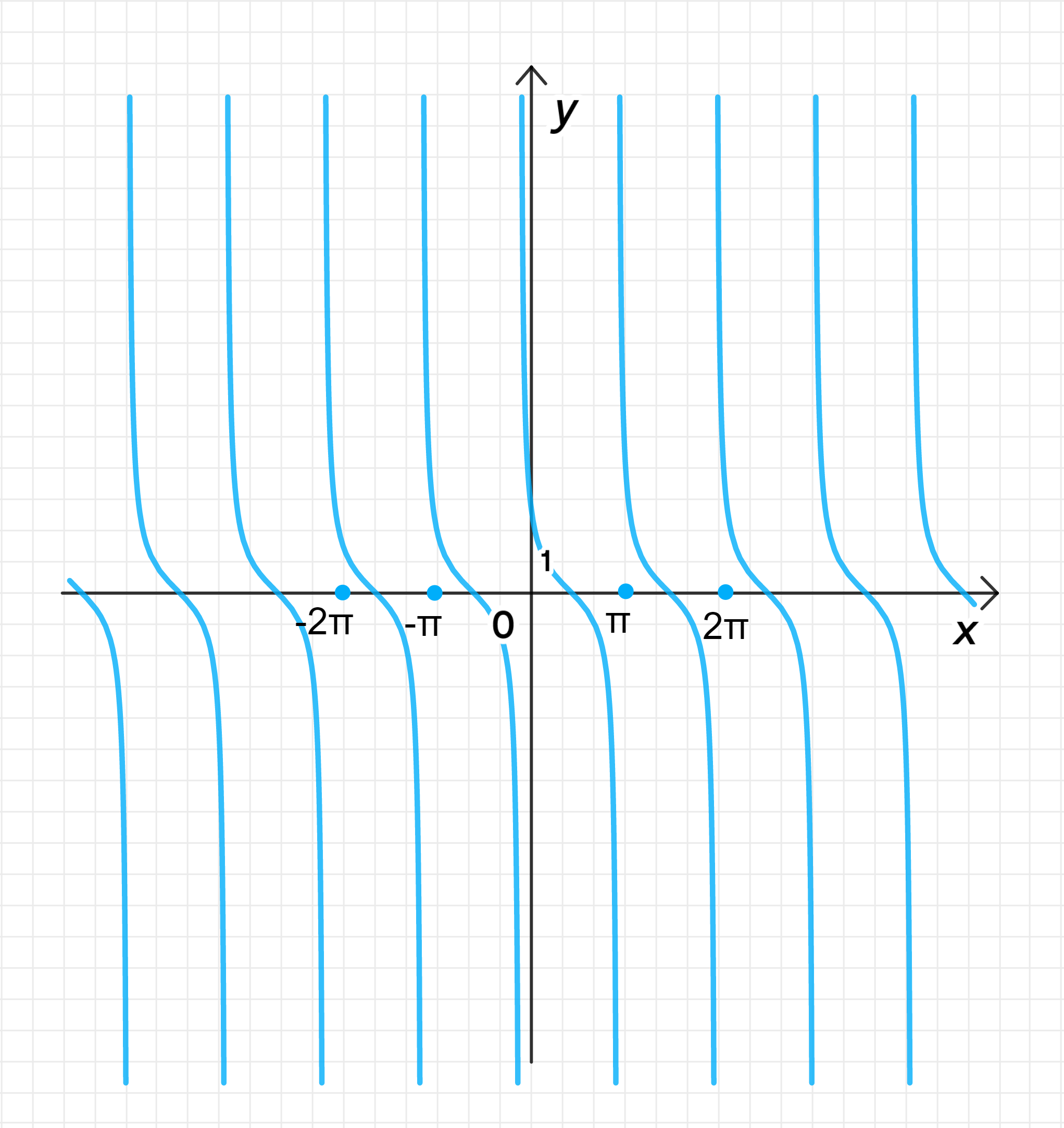
в) ;
Главная ветвь тангенсоиды имеет центр в точке ;
Ветвь лежит на интервале:
Ветвь отражена относительно прямой ;
График функции:
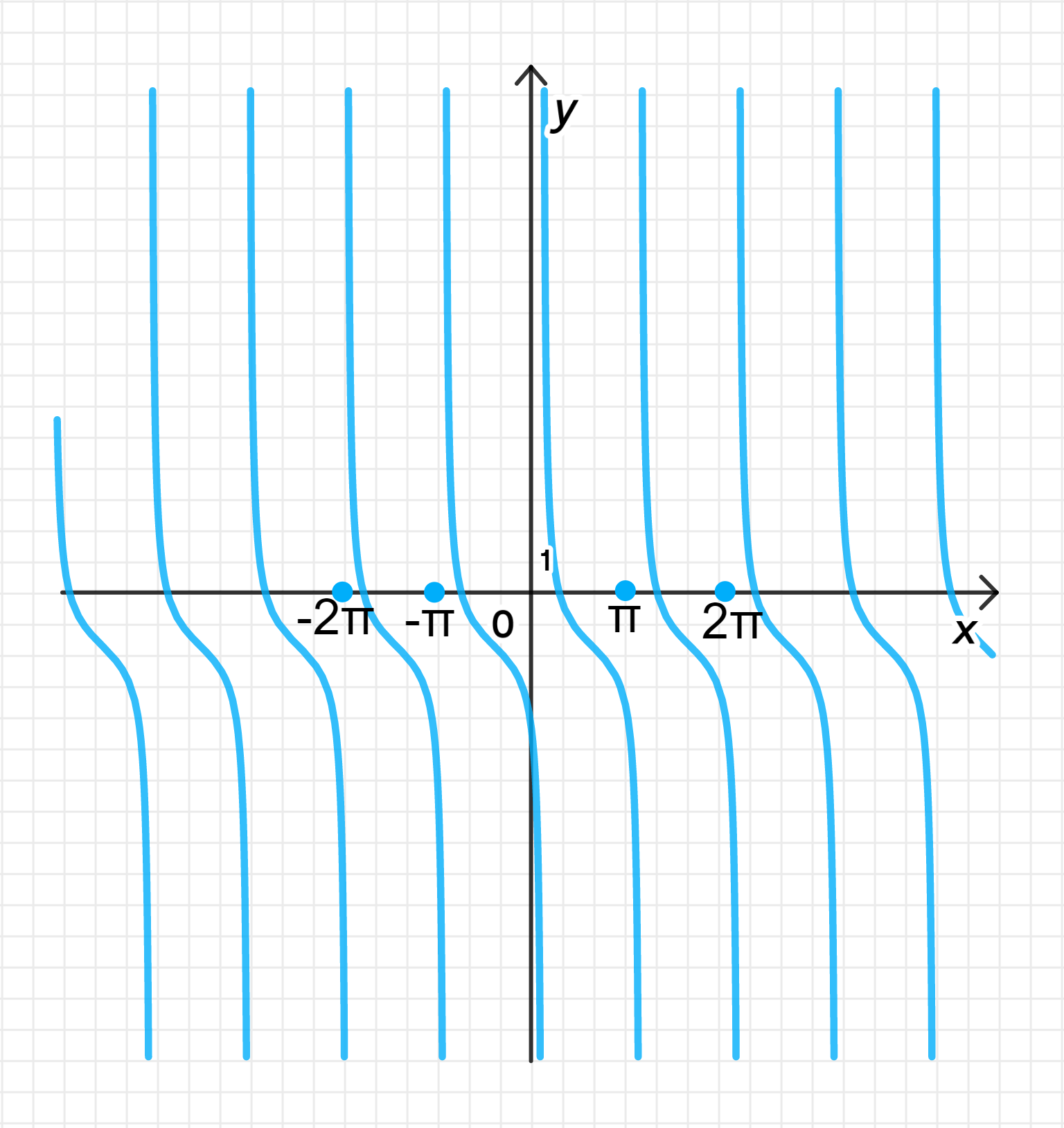
г) ;
Главная ветвь тангенсоиды имеет центр в точке ;
Ветвь лежит на интервале:
Ветвь отражена относительно прямой ;
График функции:
а) ;
1. Основная форма графика
График функции — это стандартный тангенс, который имеет вертикальные асимптоты в точках (где — целое число). Эти асимптоты возникают, потому что тангенс стремится к бесконечности при . В этом случае график проходит через начало координат и имеет период .
2. Отражение графика
В функции знак минус перед тангенсом означает, что весь график отражен относительно оси . В результате этого отражения:
- Положительные значения функции становятся отрицательными, а отрицательные — положительными.
- Асимптоты остаются на тех же местах.
- График теперь имеет нисходящий характер, а не восходящий, как у функции .
3. Центр графика
Центр (точка, через которую проходит главный участок графика) функции — это точка , так как тангенс проходит через начало координат, а отражение не сдвигает его.
4. Интервал, на котором лежит график
График функции существует на интервале , так как тангенс на этих промежутках не имеет асимптот, а на границах интервала функции стремится к бесконечности.
5. График функции
График функции будет иметь вид:
- Через точку .
- Асимптоты в точках .
- График будет нисходящим.
б) ;
1. Вертикальный сдвиг
Теперь в уравнении добавлен сдвиг на в правой части. Это означает, что весь график будет сдвинут вверх на 1 единицу, что изменит его центр.
- Если для центр был в точке , то для центр будет в точке .
2. Асимптоты
Асимптоты не изменяются, потому что вертикальные асимптоты определяются значением тангенса, а сдвиг графика вдоль оси не влияет на их положение.
3. Отражение графика
Отражение относительно оси сохраняется, так как это связано с наличием минуса перед тангенсом.
4. Интервал графика
График по-прежнему лежит на интервале , как и у предыдущей функции, так как этот интервал не зависит от сдвига вдоль оси .
5. График функции
- Новый центр графика будет в точке .
- Асимптоты на тех же местах.
- График сдвинут вверх на 1 единицу.
в) ;
1. Горизонтальный сдвиг
Здесь в функции есть сдвиг . Это означает, что график тангенсоиды будет сдвинут вправо на единиц:
- Вместо того чтобы проходить через , главный участок графика будет начинаться с точки .
- Таким образом, центр графика будет в точке .
2. Асимптоты
Положение вертикальных асимптот изменится:
- Асимпта — это значения, при которых аргумент приближается к , но сдвиг сдвигает асимптоты вправо на .
- Получаем асимптоты в точках и .
3. Отражение графика
Как и раньше, график отражен относительно оси .
4. Интервал графика
Новый интервал для графика будет:
что соответствует интервалу .
5. График функции
- Новый центр в точке .
- Асимптоты на и .
- График сдвинут вправо на .
г) ;
1. Сдвиг влево и вниз
Теперь у нас два преобразования:
- Сдвиг функции влево на , что изменяет положение главного участка графика на .
- Сдвиг вниз на 2 единицы, что делает новый центр графика в точке .
2. Асимптоты
Сдвиг влево на изменяет положение вертикальных асимптот. Для функции асимптоты находятся в точках . После сдвига влево:
- Асимптоты будут в точках и .
- После упрощения получаем асимптоты в точках и .
3. Отражение графика
График по-прежнему отражен относительно оси .
4. Интервал графика
Для нового графика интервал:
что приводит к интервалу:
5. График функции
- Новый центр в точке .
- Асимптоты в точках и .
- График сдвинут влево на и вниз на 2 единицы.