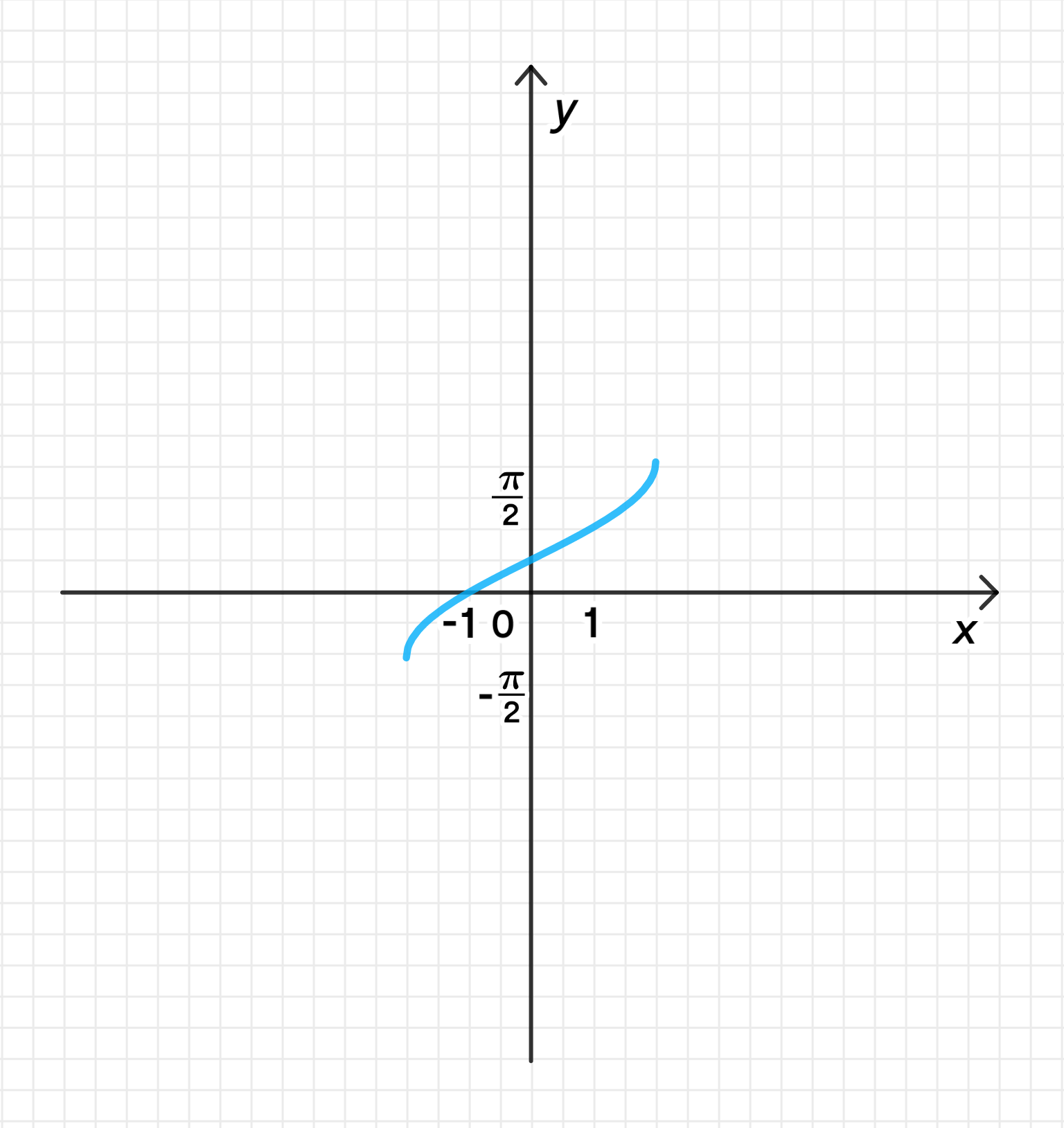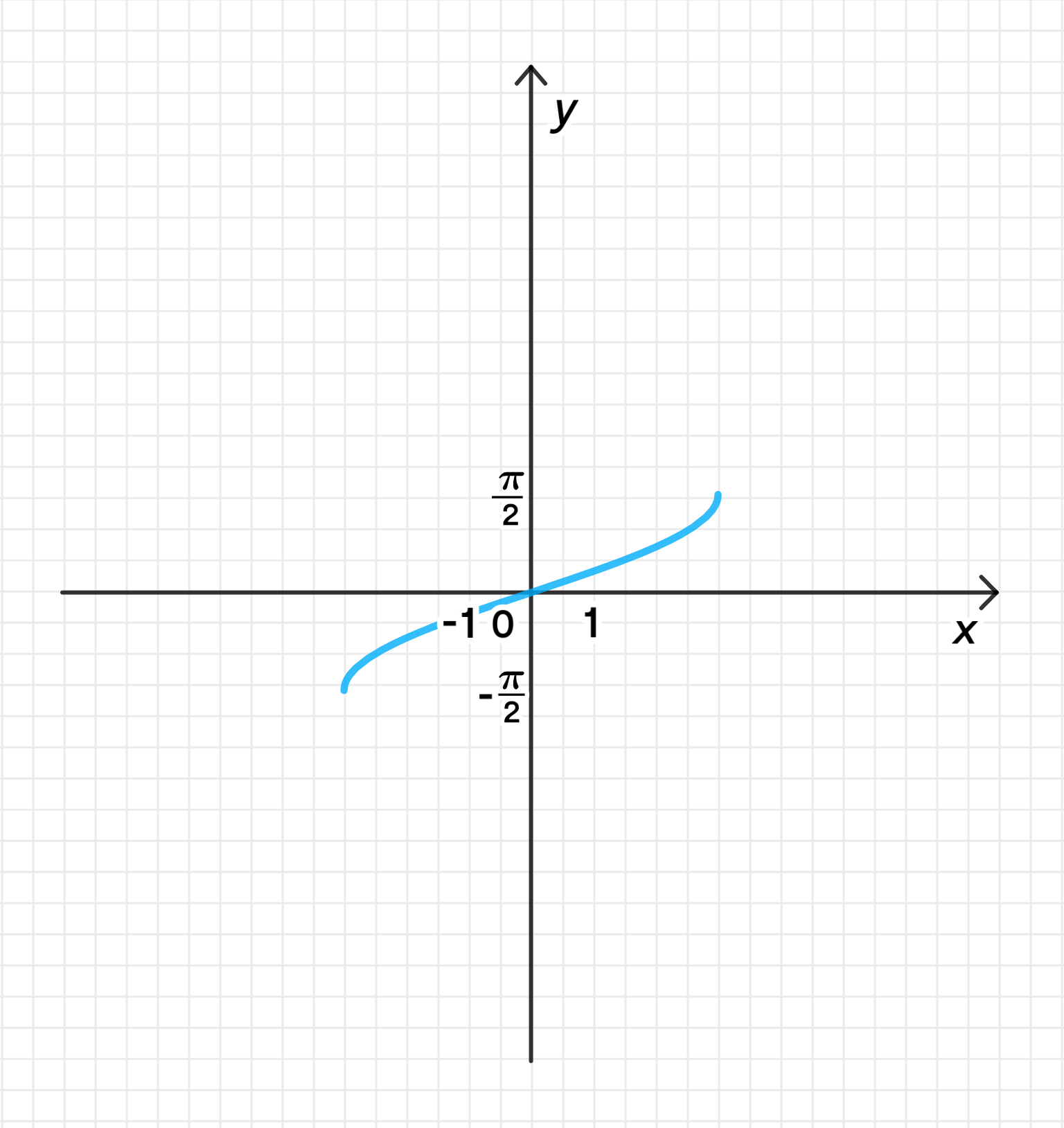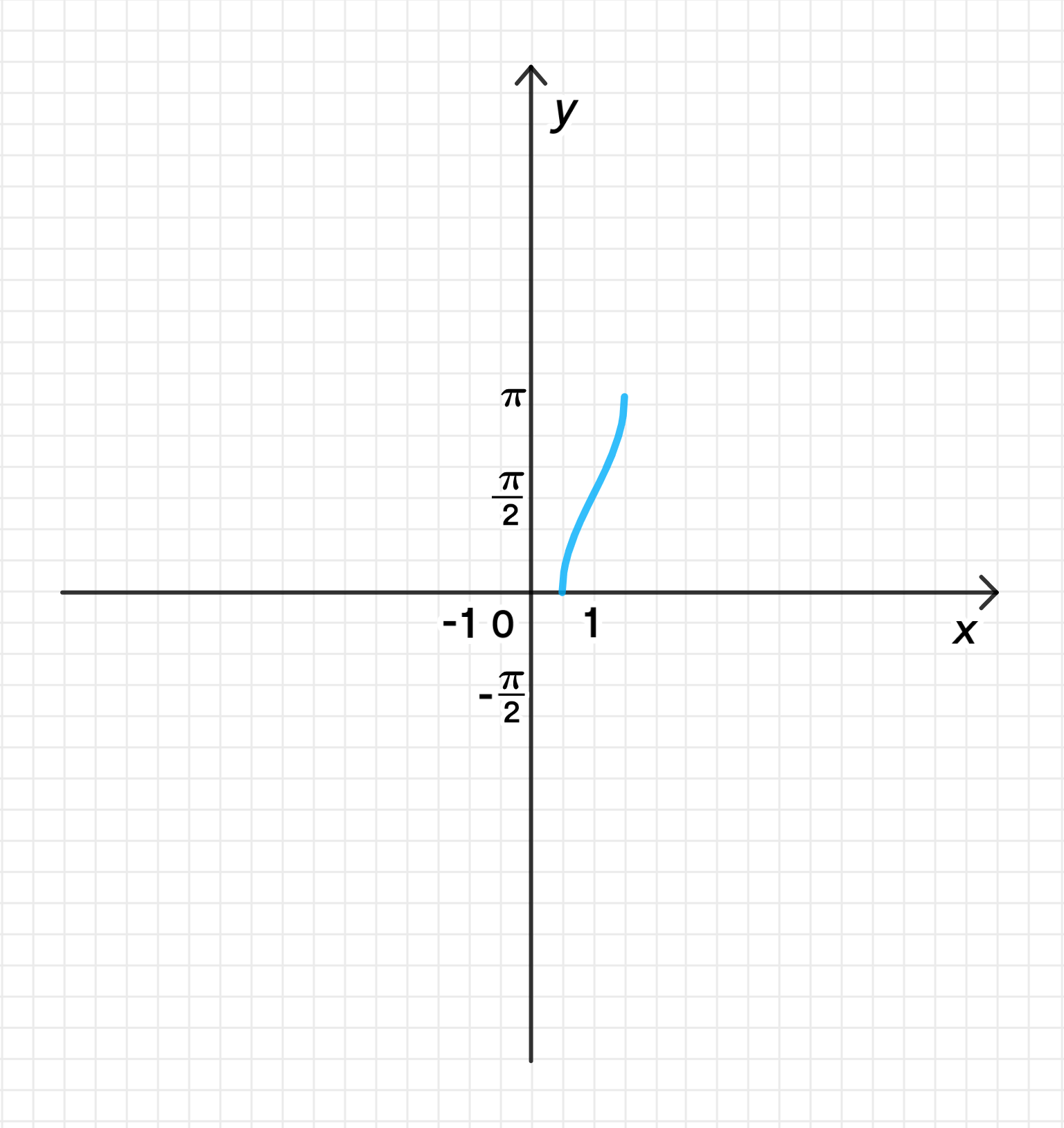Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 21.10 Профильный Уровень Мордкович — Подробные Ответы
Постройте график функции:
а) ;
б) ;
в) ;
г)
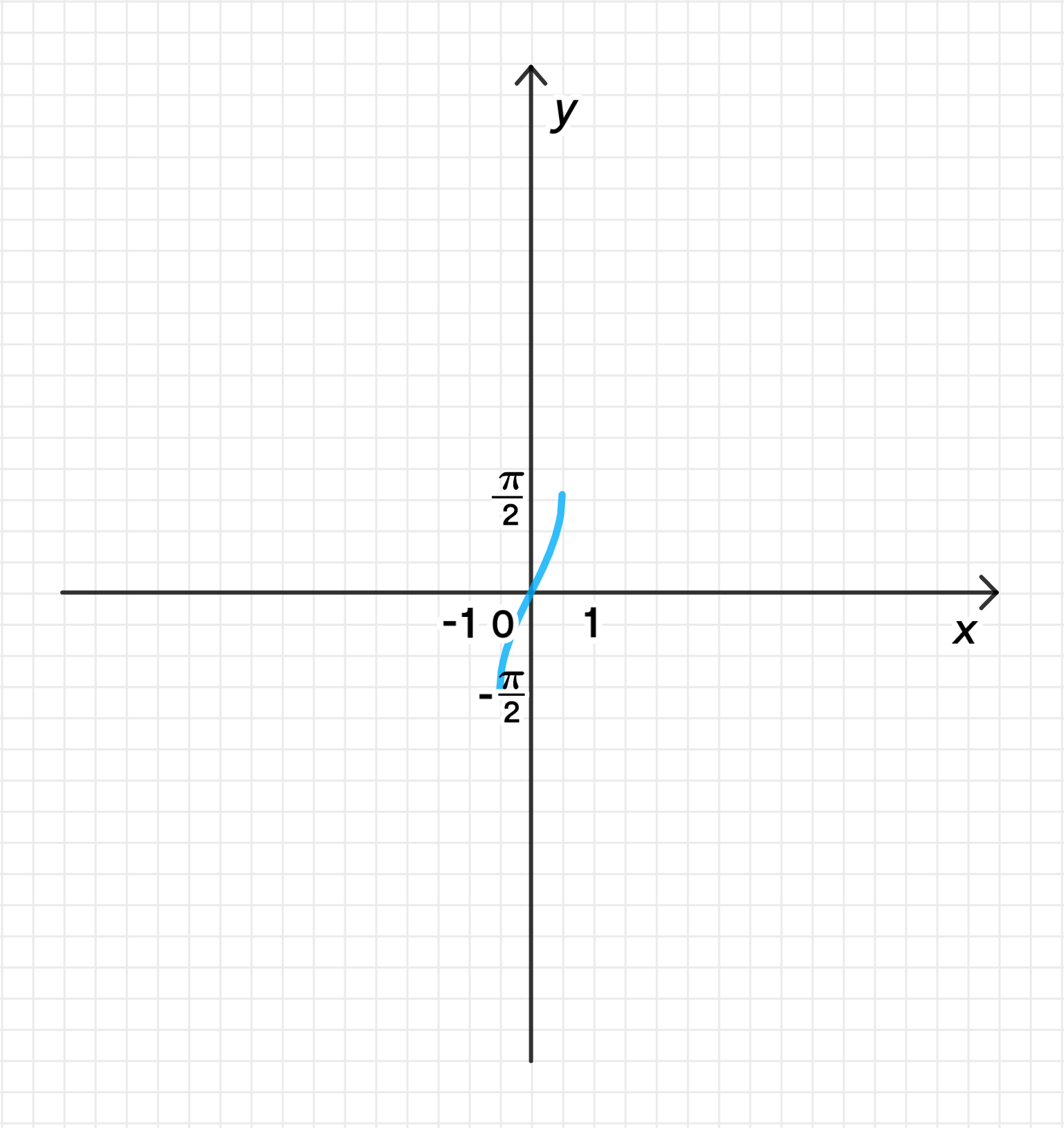
а) ;
Построим график функции ;
Сожмем его к оси с коэффициентом :
б) ;
Построим график функции ;
Растянем его от оси с коэффициентом ;
Переместим его на единиц вверх вдоль оси ординат:
в) ;
Построим график функции ;
Растянем его от оси с коэффициентом :
г) ;
Построим график функции ;
Сожмем его к оси с коэффициентом ;
Переместим его на 1 единицу вправо вдоль оси абсцисс;
Переместим его на единиц вверх вдоль оси ординат:
а)
Построим график функции :
Функция определена на интервале , так как для значений вне этого диапазона синус не может быть обратным.
График функции — это плавная кривая, начинающаяся в точке и заканчивающаяся в точке .
На данном графике значение функции растет от до при увеличении от до .
Сожмем график функции по оси с коэффициентом :
В данном случае нам нужно изменить функцию таким образом, чтобы она сжималась по оси . Это можно осуществить, умножив аргумент функции на коэффициент , то есть получаем новую функцию:
Таким образом, аргумент функции увеличивается в два раза. Это означает, что точки на графике будут сдвигаться по оси , но сам график будет сжаться вдоль оси .
Рассмотрим пределы изменения функции. Если при для значение равно , то теперь для функции значение будет достигать при , а при функция уже выходит за пределы области определения.
б)
Построим график функции :
Как уже было сказано, график функции — это плавная кривая, определенная на интервале . Он проходит от до .
Растянем график функции от оси с коэффициентом :
Здесь у нас будет растяжение по оси . Это означает, что аргумент функции будет уменьшаться. Вместо мы используем . Таким образом, наша функция становится:
График растянется вдоль оси , и теперь будет достигать значений при , что расширяет область определения функции.
Переместим график на единиц вверх вдоль оси ординат:
В последнем шаге мы добавляем постоянное значение к функции:
Это означает, что весь график будет сдвинут на единиц вверх вдоль оси . При этом не изменяются значения , только значение увеличивается на по всей длине графика.
в)
Построим график функции :
Определяем график функции на интервале , и она будет начинаться в точке и заканчиваться в точке .
Растянем график функции от оси с коэффициентом :
В этом случае аргумент функции изменяется, и мы делим на 3:
Таким образом, график растягивается по оси , и область определения функции также расширяется. Если раньше при мы имели значение , то теперь это значение будет достигаться при .
г)
Построим график функции :
Как и прежде, график функции будет плавно изменяться от до .
Сожмем график по оси с коэффициентом :
Подобно первому примеру, мы сжимаем график по оси с коэффициентом 2. Это достигается заменой на , то есть:
Здесь, по аналогии с первым примером, функция будет сжата по оси , а также будет сдвигаться влево.
Переместим график на 1 единицу вправо вдоль оси абсцисс:
Внутри аргумента функции происходит сдвиг графика вправо на 1 единицу. Это достигается добавлением к , и теперь аргумент функции будет .
Переместим график на единиц вверх вдоль оси ординат:
Последний шаг — это вертикальный сдвиг графика на единиц вверх, что можно выразить как добавление к функции:
Таким образом, весь график будет сдвинут на единиц вверх.