ГДЗ по Алгебре 10 Класс Номер 21.11 Профильный Уровень Мордкович — Подробные Ответы

Постройте и прочитайте график функции:

а) $y=\{\begin{array}{ll}\frac{\pi x}{2},& \text{если }x<-1\\ \arcsin x,& \text{если }-1\le x\le 1\\ \frac{\pi }{2},& \text{если }x>1\end{array}$

б) $y=\{\begin{array}{ll}\arcsin x,& \text{если }-1\le x\le 0\\ -\arcsin x,& \text{если }0<x\le 1\\ (x-1{)}^2-\frac{\pi }{2},& \text{если }1<x\le 3\end{array}$

а) $y = \begin{cases} \frac{\pi x}{2}, & \text{если } x < -1 \\ \arcsin x, & \text{если } -1 \leq x \leq 1; \\ \frac{\pi}{2}, & \text{если } x > 1 \end{cases}$

$y = \frac{\pi x}{2}$ — уравнение прямой:

$$\begin{array}{|c|c|c|} \hline x & -2 & -1 \\ \hline y & -\pi & -\frac{\pi}{2} \\ \hline \end{array}$$

$y = \arcsin x$ — обратная функция:

$$\begin{array}{|c|c|c|} \hline x & -1 & 1 \\ \hline y & -\frac{\pi}{2} & \frac{\pi}{2} \\ \hline \end{array}$$

$y = \frac{\pi}{2}$ — уравнение прямой;

Графики функций:

Свойства функции:

• Область определения: $D(f) = (-\infty; +\infty)$;
• Множество значений: $E(f) = \left( -\infty; \frac{\pi}{2} \right]$;
• Возрастает на $(-\infty; 1]$;
• Постоянна на $[1; +\infty)$;
• $f(x) > 0$ на $(0; +\infty)$;
• $f(x) < 0$ на $(-\infty; 0)$;
• Функция ни четная, ни нечетная;
• Функция не является периодической;

б) $y = \begin{cases} \arcsin x, & \text{если } -1 \leq x \leq 0 \\ -\arcsin x, & \text{если } 0 < x \leq 1 \\ (x-1)^2 — \frac{\pi}{2}, & \text{если } 1 < x \leq 3 \end{cases}$

$y = \arcsin x$ — обратная функция:

$$\begin{array}{|c|c|c|} \hline x & -1 & 0 \\ \hline y & -\frac{\pi}{2} & 0 \\ \hline \end{array}$$

$y = -\arcsin x$ — обратная функция:

$$\begin{array}{|c|c|c|} \hline x & 0 & 1 \\ \hline y & 0 & -\frac{\pi}{2} \\ \hline \end{array}$$

$y = (x-1)^2 — \frac{\pi}{2}$ — уравнение параболы:

$$x_0 = 1, \quad y_0 = -\frac{\pi}{2};$$ $$\begin{array}{|c|c|c|c|} \hline x & 1 & 2 & 3 \\ \hline y & -\frac{\pi}{2} & \approx -\frac{\pi}{6} & \approx \frac{5\pi}{6} \\ \hline \end{array}$$

Графики функций:

Свойства функции:

• Область определения: $D(f) = [-1; 3]$;
• Множество значений: $E(f) = \left[ -\frac{\pi}{2}; 4 — \frac{\pi}{2} \right]$;
• Возрастает на $[-1; 0] \cup [1; 3]$;
• Убывает на $[0; 1]$;
• $f(x) > 0$ на $\left( 1 + \sqrt{\frac{\pi}{2}}; 3 \right]$;
• $f(x) < 0$ на $[-1; 0) \cup \left( 0; 1 + \sqrt{\frac{\pi}{2}} \right)$;
• Функция ни четная, ни нечетная;
• Функция не является периодической

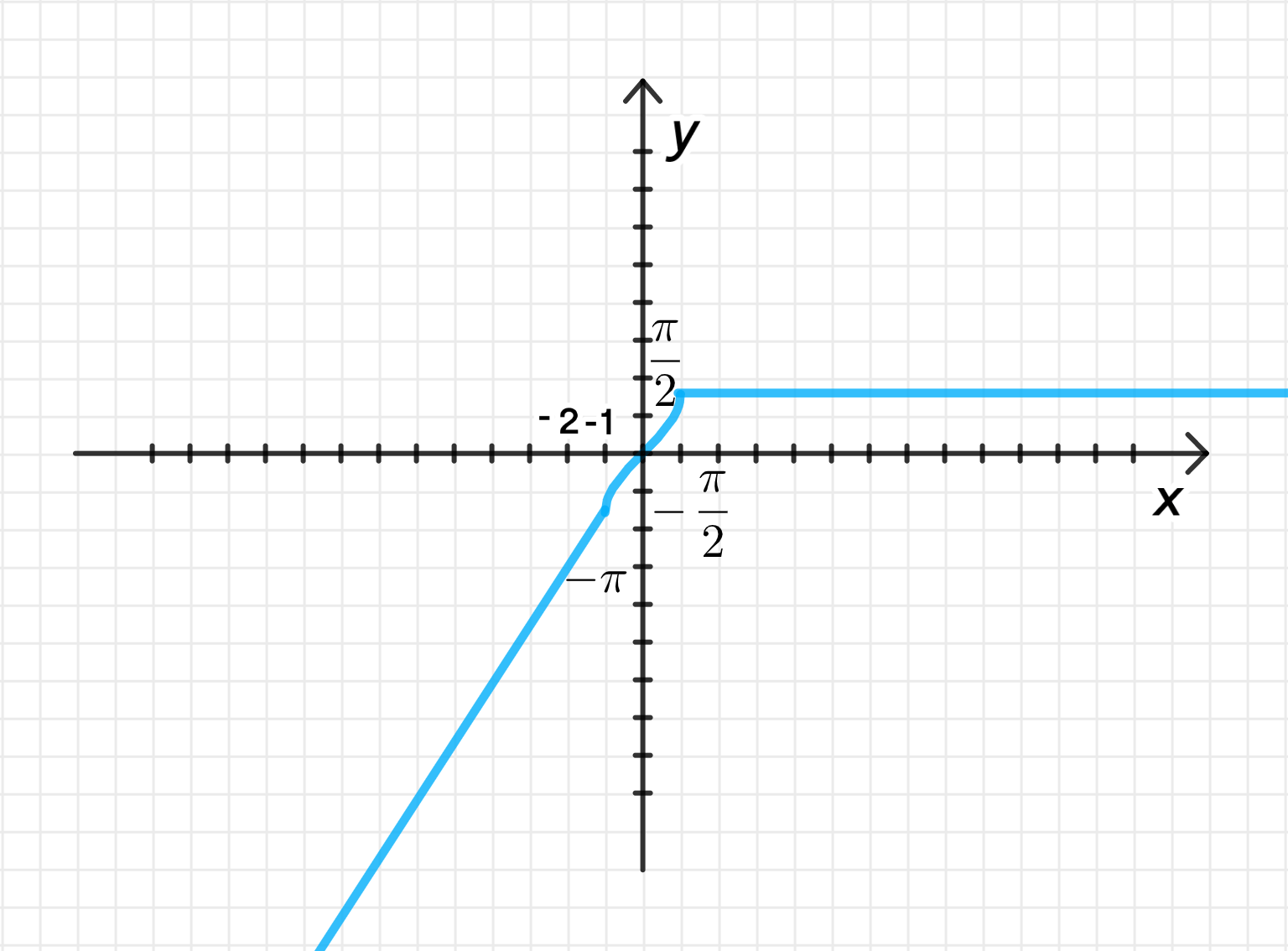
а) $y = \begin{cases} \frac{\pi x}{2}, & \text{если } x < -1 \\ \arcsin x, & \text{если } -1 \leq x \leq 1; \\ \frac{\pi}{2}, & \text{если } x > 1 \end{cases}$

1) $y = \frac{\pi x}{2}$ — уравнение прямой:

Для $x < -1$ функция задана как линейная, и её график представляет собой прямую.

• Когда $x = -2$, мы подставляем это значение в выражение для $y$:

  $$y = \frac{\pi \cdot (-2)}{2} = -\pi$$

• Когда $x = -1$, подставляем это значение:

  $$y = \frac{\pi \cdot (-1)}{2} = -\frac{\pi}{2}$$

Таким образом, для этого участка функции, когда $x \in (-\infty; -1)$, значения $y$ будут вычисляться по формуле $y = \frac{\pi x}{2}$, а на отрезке $x = -2$ и $x = -1$ мы получаем значения $y = -\pi$ и $y = -\frac{\pi}{2}$ соответственно.

В результате таблица значений выглядит следующим образом:

$$\begin{array}{|c|c|c|} \hline x & -2 & -1 \\ \hline y & -\pi & -\frac{\pi}{2} \\ \hline \end{array}$$

2) $y = \arcsin x$ — обратная функция:

Для $-1 \leq x \leq 1$, функция $y = \arcsin x$ представляет собой обратную функцию к $y = \sin x$. Эта функция определена на отрезке $[-1, 1]$.

• Когда $x = -1$, мы подставляем это значение:

  $$y = \arcsin(-1) = -\frac{\pi}{2}$$

• Когда $x = 1$, подставляем:

  $$y = \arcsin(1) = \frac{\pi}{2}$$

Таким образом, для этого участка функции, значения $y$ будут вычисляться по формуле $y = \arcsin x$, а на отрезке $x = -1$ и $x = 1$ мы получаем значения $y = -\frac{\pi}{2}$ и $y = \frac{\pi}{2}$ соответственно.

Таблица значений:

$$\begin{array}{|c|c|c|} \hline x & -1 & 1 \\ \hline y & -\frac{\pi}{2} & \frac{\pi}{2} \\ \hline \end{array}$$

3) $y = \frac{\pi}{2}$ — уравнение прямой:

Для $x > 1$, функция $y = \frac{\pi}{2}$ представляет собой горизонтальную прямую, которая равна постоянной величине $\frac{\pi}{2}$.

4) Графики функций:

5) Свойства функции:

• Область определения $D(f)$: функция определена на всей числовой прямой, то есть $(-\infty; +\infty)$.
• Множество значений $E(f)$: значения функции ограничены сверху значением $\frac{\pi}{2}$, то есть множество значений $E(f) = (-\infty; \frac{\pi}{2}]$.
• Возрастание: функция возрастает на интервале $(-\infty; 1]$, потому что на этом отрезке у нас линейный рост и обратная функция синуса.
• Постоянство: на интервале $[1; +\infty)$ функция постоянна, так как $y = \frac{\pi}{2}$.
• Значения функции: функция принимает положительные значения для $x > 0$, и отрицательные для $x < 0$. То есть $f(x) > 0$ на $(0; +\infty)$, и $f(x) < 0$ на $(-\infty; 0)$.
• Четность/Нечетность: функция не является четной или нечетной, так как её график не симметричен относительно оси $y$ или начала координат.
• Периодичность: функция не является периодической, так как её график не повторяется через равные интервалы.

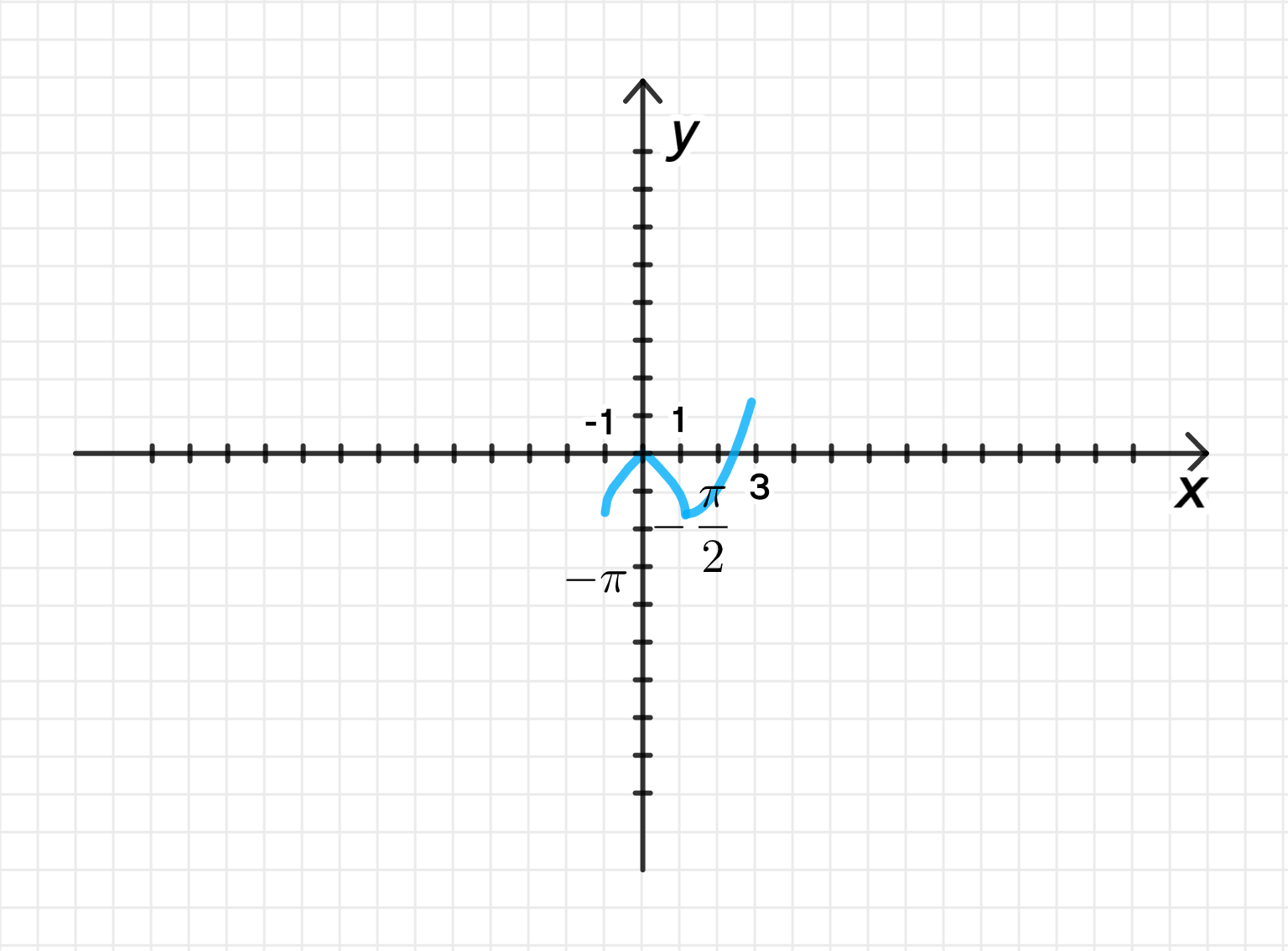
б) $y = \begin{cases} \arcsin x, & \text{если } -1 \leq x \leq 0 \\ -\arcsin x, & \text{если } 0 < x \leq 1 \\ (x-1)^2 — \frac{\pi}{2}, & \text{если } 1 < x \leq 3 \end{cases}$

1) $y = \arcsin x$ — обратная функция:

Для $-1 \leq x \leq 0$, эта часть функции является обратной функцией синуса.

• Когда $x = -1$, подставляем:

  $$y = \arcsin(-1) = -\frac{\pi}{2}$$

• Когда $x = 0$, подставляем:

  $$y = \arcsin(0) = 0$$

Таблица значений:

$$\begin{array}{|c|c|c|} \hline x & -1 & 0 \\ \hline y & -\frac{\pi}{2} & 0 \\ \hline \end{array}$$

2) $y = -\arcsin x$ — обратная функция:

Для $0 < x \leq 1$, эта часть функции является инвертированной обратной функцией синуса.

• Когда $x = 0$, подставляем:

  $$y = -\arcsin(0) = 0$$

• Когда $x = 1$, подставляем:

  $$y = -\arcsin(1) = -\frac{\pi}{2}$$

Таблица значений:

$$\begin{array}{|c|c|c|} \hline x & 0 & 1 \\ \hline y & 0 & -\frac{\pi}{2} \\ \hline \end{array}$$

3) $y = (x-1)^2 — \frac{\pi}{2}$ — уравнение параболы:

Для $1 < x \leq 3$, эта часть функции задаёт параболу.

• Для вершины параболы при $x = 1$ имеем:

  $$y = (1 — 1)^2 — \frac{\pi}{2} = -\frac{\pi}{2}$$

• Для $x = 2$:

  $$y = (2 — 1)^2 — \frac{\pi}{2} = 1 — \frac{\pi}{2} \approx -\frac{\pi}{6}$$

• Для $x = 3$:

  $$y = (3 — 1)^2 — \frac{\pi}{2} = 4 — \frac{\pi}{2} \approx \frac{5\pi}{6}$$

Таблица значений:

$$\begin{array}{|c|c|c|c|} \hline x & 1 & 2 & 3 \\ \hline y & -\frac{\pi}{2} & \approx -\frac{\pi}{6} & \approx \frac{5\pi}{6} \\ \hline \end{array}$$

4) Графики функций:

5) Свойства функции:

• Область определения $D(f)$: функция определена на интервале $[-1, 3]$, так как за пределами этого интервала части функции не определены.
• Множество значений $E(f)$: наибольшее значение функции достигается на правом конце параболы, то есть $E(f) = \left[ -\frac{\pi}{2}; 4 — \frac{\pi}{2} \right]$.
• Возрастание: функция возрастает на $[-1; 0] \cup [1; 3]$, так как на этих интервалах части функции либо растут (парабола), либо возрастает $\arcsin x$.
• Убывание: функция убывает на $[0; 1]$, так как на этом интервале $y = -\arcsin x$.
• Значения функции: $f(x) > 0$ на интервале $\left( 1 + \sqrt{\frac{\pi}{2}}; 3 \right]$ и $f(x) < 0$ на интервале $[-1; 0) \cup \left( 0; 1 + \sqrt{\frac{\pi}{2}} \right)$.
• Четность/Нечетность: функция не является четной или нечетной.
• Периодичность: функция не является периодической, так как её график не повторяется.