ГДЗ по Алгебре 10 Класс Номер 21.12 Профильный Уровень Мордкович — Подробные Ответы

Постройте график функции:

а) $y = 3|\arcsin x| — \arcsin x$;

б) $y = \arcsin x + |\arcsin x|$;

в) $y = \left| \arcsin x — \frac{\pi}{3} \right|$;

г) $y=-\arcsin \mathrm{\mid }x-2\mathrm{\mid }=\arcsin (-\mathrm{\mid }x-2\mathrm{\mid })$

а) $y = 3|\arcsin x| — \arcsin x$;

Если $x \geq 0$, тогда:

$$y = 3\arcsin x — \arcsin x = 2\arcsin x;$$

Если $x < 0$, тогда:

$$y = -3\arcsin x — \arcsin x = -4\arcsin x;$$

График функции:

б) $y = \arcsin x + |\arcsin x|$;

Если $x \geq 0$, тогда:

$$y = \arcsin x + \arcsin x = 2\arcsin x;$$

Если $x < 0$, тогда:

$$y = -\arcsin x + \arcsin x = 0;$$

График функции:

в) $y = \left| \arcsin x — \frac{\pi}{3} \right|$;

Построим график функции $y = \arcsin x$;

Переместим его на $\frac{\pi}{3}$ единиц вниз вдоль оси ординат;

Отразим относительно оси $Ox$ часть графика, лежащую по ней:

г) $y = -\arcsin |x-2| = \arcsin(-|x-2|)$;

Построим график функции $y = \arcsin x$;

Переместим его на 2 единицы вправо вдоль оси абсцисс;

Уберем часть графика, лежащую справа от прямой $x = 2$;

Отразим относительно нее часть графика, лежащую слева:

а) $y = 3|\arcsin x| — \arcsin x$;

1) Рассмотрим случай, когда $x \geq 0$:

Для $x \geq 0$ абсолютное значение $|\arcsin x| = \arcsin x$, так как $\arcsin x \geq 0$ на отрезке $[0, 1]$. Тогда выражение для функции примет вид:

$$y = 3\arcsin x — \arcsin x = 2\arcsin x.$$

То есть, на интервале $x \in [0, 1]$ функция будет представлять собой удвоенную обратную функцию синуса $y = 2\arcsin x$.

2) Рассмотрим случай, когда $x < 0$:

Для $x < 0$ абсолютное значение $|\arcsin x| = -\arcsin x$, так как $\arcsin x \leq 0$ на отрезке $[-1, 0)$. Тогда выражение для функции примет вид:

$$y = 3(-\arcsin x) — \arcsin x = -3\arcsin x — \arcsin x = -4\arcsin x.$$

То есть, на интервале $x \in [-1, 0)$ функция будет представлять собой $y = -4\arcsin x$.

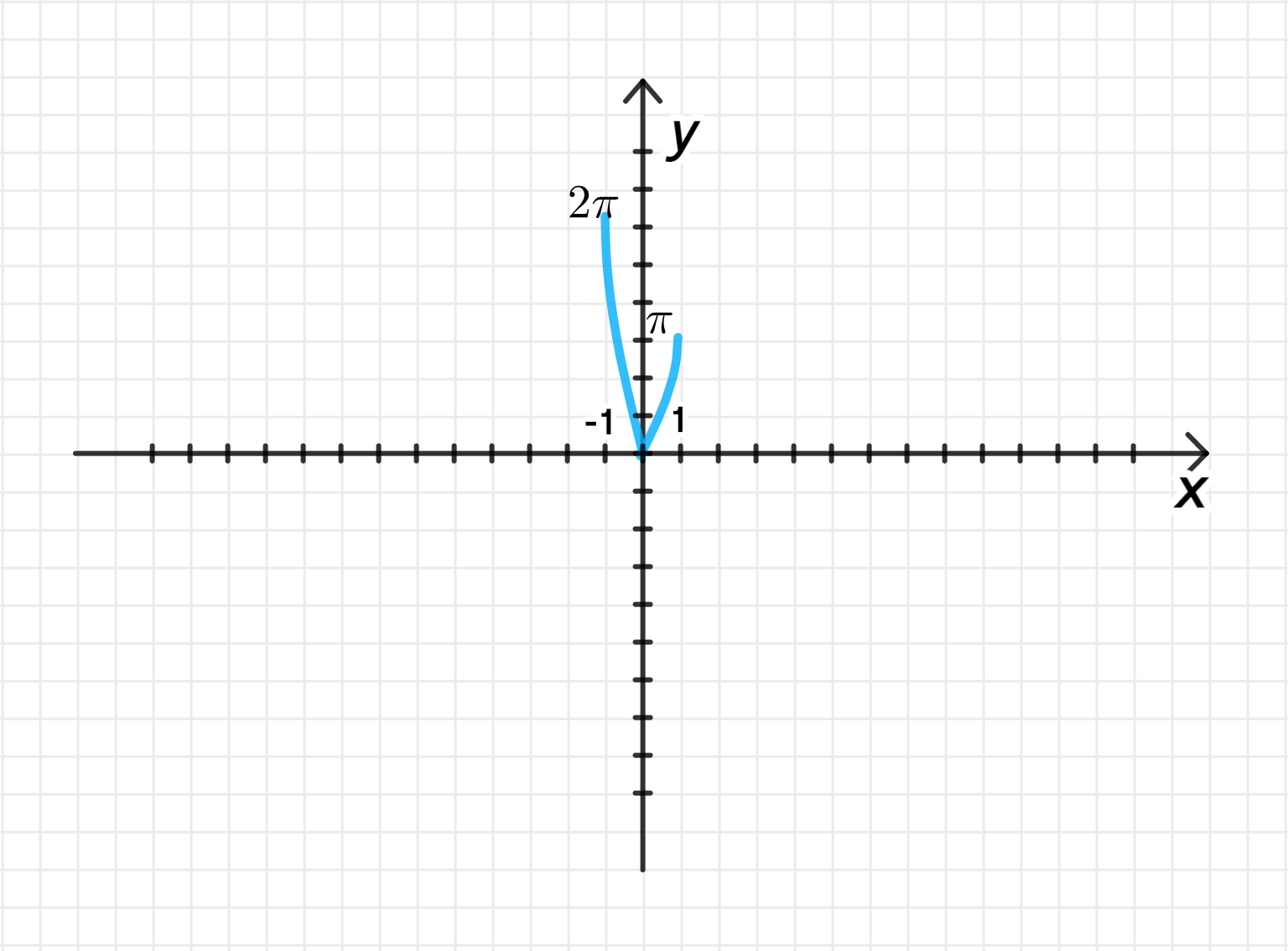
3) График функции:

• Для $x \geq 0$ график будет иметь вид функции $y = 2\arcsin x$, которая возрастает от 0 до $\frac{\pi}{2}$ на интервале $[0, 1]$.
• Для $x < 0$ график будет иметь вид функции $y = -4\arcsin x$, которая убывает от 0 до $-\frac{\pi}{2}$ на интервале $[-1, 0)$.

График функции будет симметричен относительно оси $Ox$, но с разными коэффициентами для положительной и отрицательной части.

б) $y = \arcsin x + |\arcsin x|$;

1) Рассмотрим случай, когда $x \geq 0$:

Для $x \geq 0$ опять же $|\arcsin x| = \arcsin x$, потому что $\arcsin x \geq 0$. Тогда функция примет вид:

$$y = \arcsin x + \arcsin x = 2\arcsin x.$$

Таким образом, на интервале $x \in [0, 1]$ функция будет представлять собой $y = 2\arcsin x$, которая возрастает от 0 до $\frac{\pi}{2}$.

2) Рассмотрим случай, когда $x < 0$:

Для $x < 0$, $|\arcsin x| = -\arcsin x$, так как $\arcsin x \leq 0$ на отрезке $[-1, 0)$. Тогда выражение для функции будет:

$$y = \arcsin x + (-\arcsin x) = 0.$$

То есть, на интервале $x \in [-1, 0)$ функция будет постоянной и равной 0.

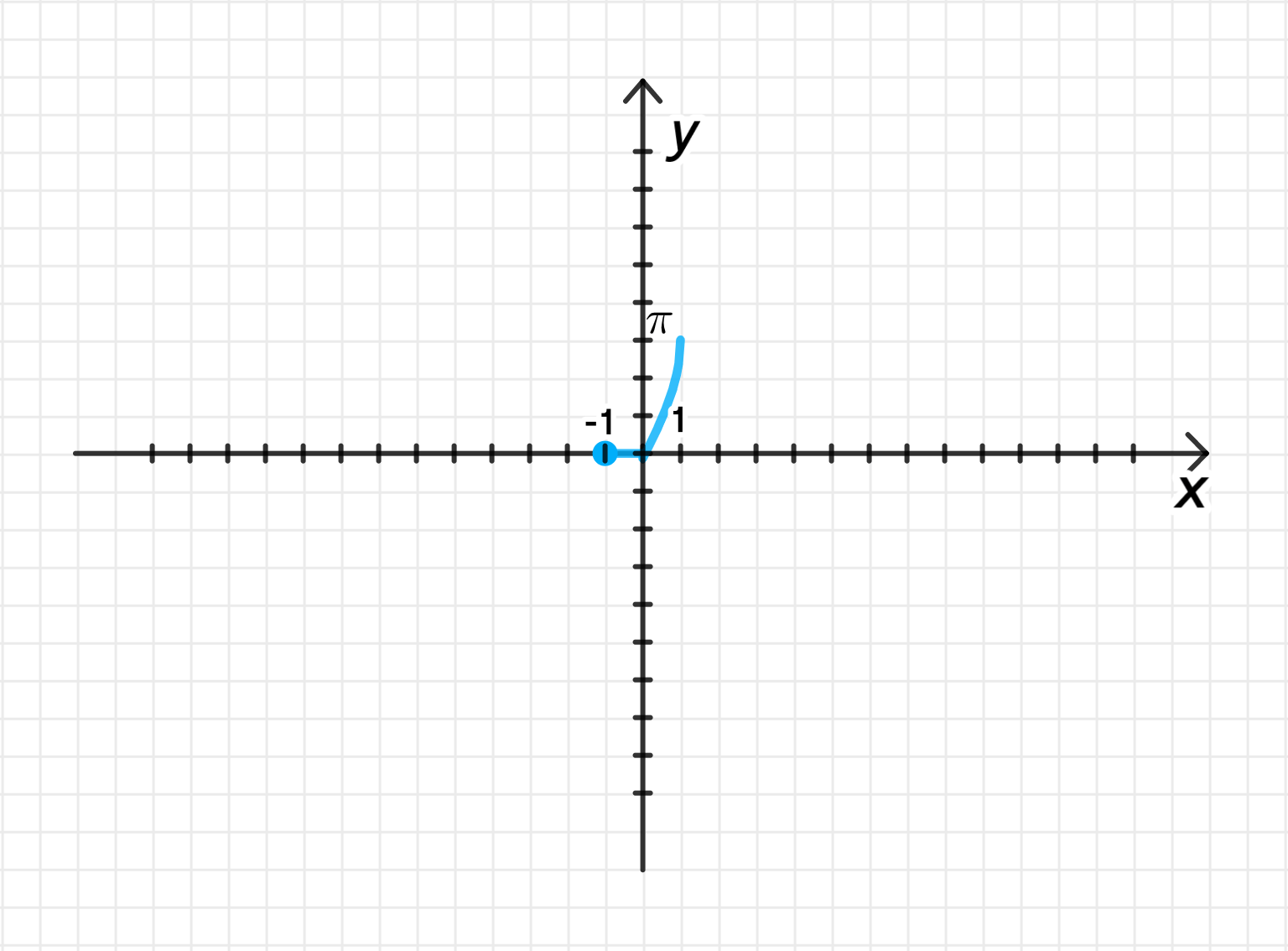
3) График функции:

• Для $x \geq 0$ график будет совпадать с графиком $y = 2\arcsin x$, возрастающим от 0 до $\frac{\pi}{2}$ на интервале $[0, 1]$.
• Для $x < 0$ график будет горизонтальной прямой $y = 0$, так как $\arcsin x + |\arcsin x| = 0$ для всех $x \in [-1, 0)$.

График будет симметричен относительно оси $Oy$, где на положительной части график будет расти, а на отрицательной части будет лежать на оси $Ox$.

в) $y = \left| \arcsin x — \frac{\pi}{3} \right|$;

1) Построим график функции $y = \arcsin x$:

График функции $y = \arcsin x$ — это возрастающая кривая, проходящая через точки $(-1, -\frac{\pi}{2})$ и $(1, \frac{\pi}{2})$.

2) Переместим его на $\frac{\pi}{3}$ единиц вниз вдоль оси ординат:

После смещения графика на $\frac{\pi}{3}$ единиц вниз, новые значения функции будут вычисляться как $y = \arcsin x — \frac{\pi}{3}$. График будет опущен вниз на $\frac{\pi}{3}$, но сохраняет свою форму.

3) Отразим относительно оси $Ox$ часть графика, лежащую по ней:

Так как мы применяем модуль, то отрицательные значения функции будут превращаться в положительные. Это означает, что для всех значений $y$, меньше $0$, будет происходить отражение относительно оси $Ox$, и на графике функции не будет отрицательных значений.

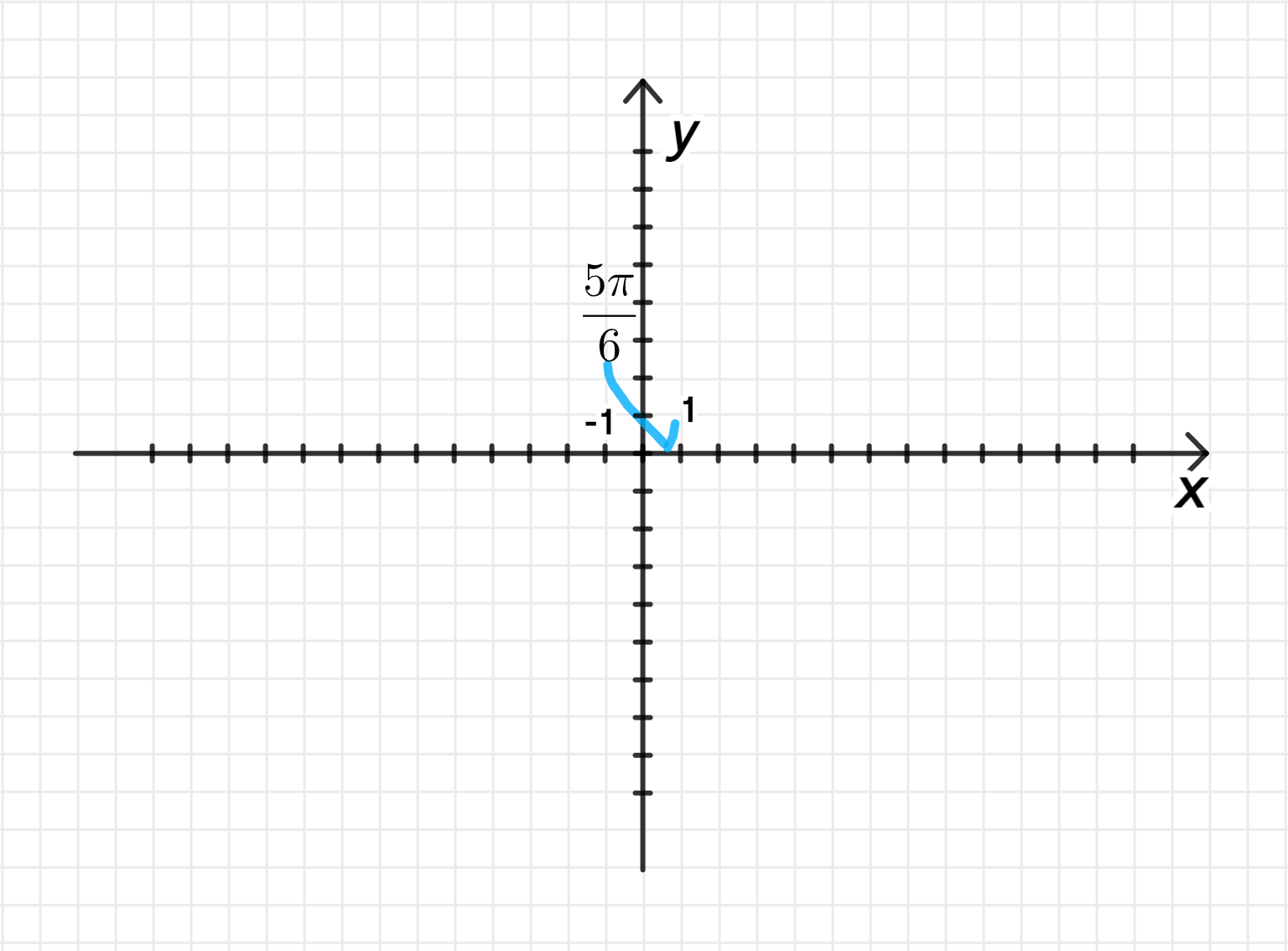
График будет представлять собой две части:

• На интервале $x \in [-1, 1]$, когда $\arcsin x — \frac{\pi}{3} \geq 0$, график будет совпадать с графиком $y = \arcsin x — \frac{\pi}{3}$.
• На интервале $x \in [-1, 1]$, когда $\arcsin x — \frac{\pi}{3} < 0$, график будет отзеркален относительно оси $Ox$.

График будет иметь форму «V», отраженную относительно оси $Ox$, и вершина будет находиться в точке, где $\arcsin x = \frac{\pi}{3}$, то есть $x = \sin\left(\frac{\pi}{3}\right) = \frac{\sqrt{3}}{2}$.

г) $y = -\arcsin |x-2| = \arcsin(-|x-2|)$;

1) Построим график функции $y = \arcsin x$:

График функции $y = \arcsin x$ — это стандартный график обратной функции синуса, возрастающая кривая, проходящая через $(-1, -\frac{\pi}{2})$ и $(1, \frac{\pi}{2})$.

2) Переместим его на 2 единицы вправо вдоль оси абсцисс:

После смещения функции на 2 единицы вправо, график будет сдвигаться вдоль оси $Ox$ на 2 единицы. То есть, теперь точка $x = 0$ будет соответствовать точке $x = 2$, а график будет выглядеть так, как будто он начинается с $x = 2$.

3) Уберем часть графика, лежащую справа от прямой $x = 2$:

Поскольку функция задана через $|x-2|$, то для $x > 2$ функция принимает отрицательные значения внутри аргумента $\arcsin(-|x-2|)$. Мы убираем эту часть графика, так как $\arcsin(x)$ определена только для значений $-1 \leq x \leq 1$.

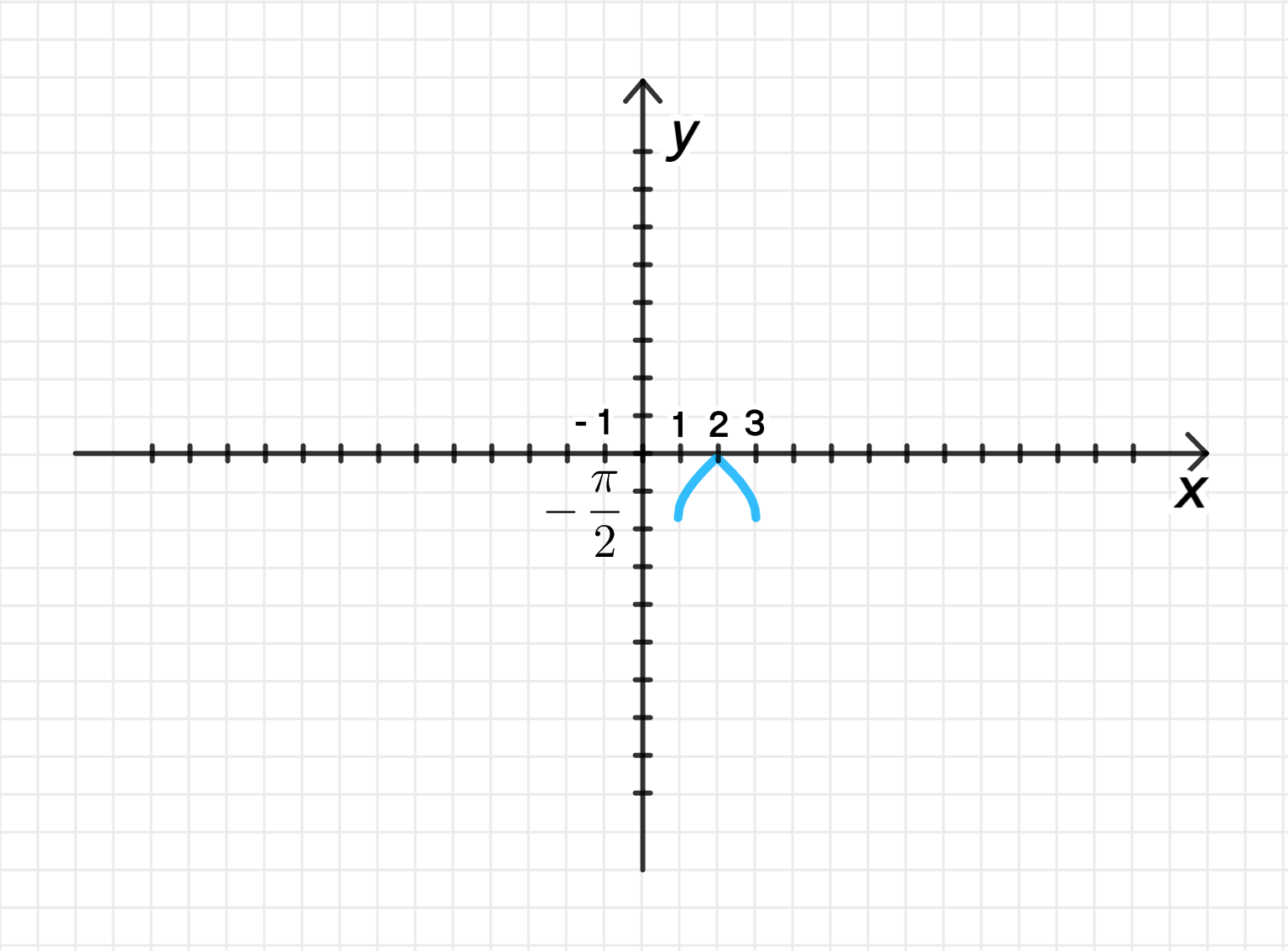
4) Отразим относительно неё часть графика, лежащую слева:

График функции $y = -\arcsin |x-2|$ будет зеркально отражён относительно оси $x = 2$ для значений $x \in (1, 2]$, так как $\arcsin(-|x-2|)$ отрицает значения для $|x-2|$. Эта часть графика будет симметрична по отношению к вертикальной прямой, проходящей через $x = 2$.

Таким образом, результат будет содержать отражённый график функции $y = \arcsin x$ в районе оси $x = 2$, с ограничениями на область определения.