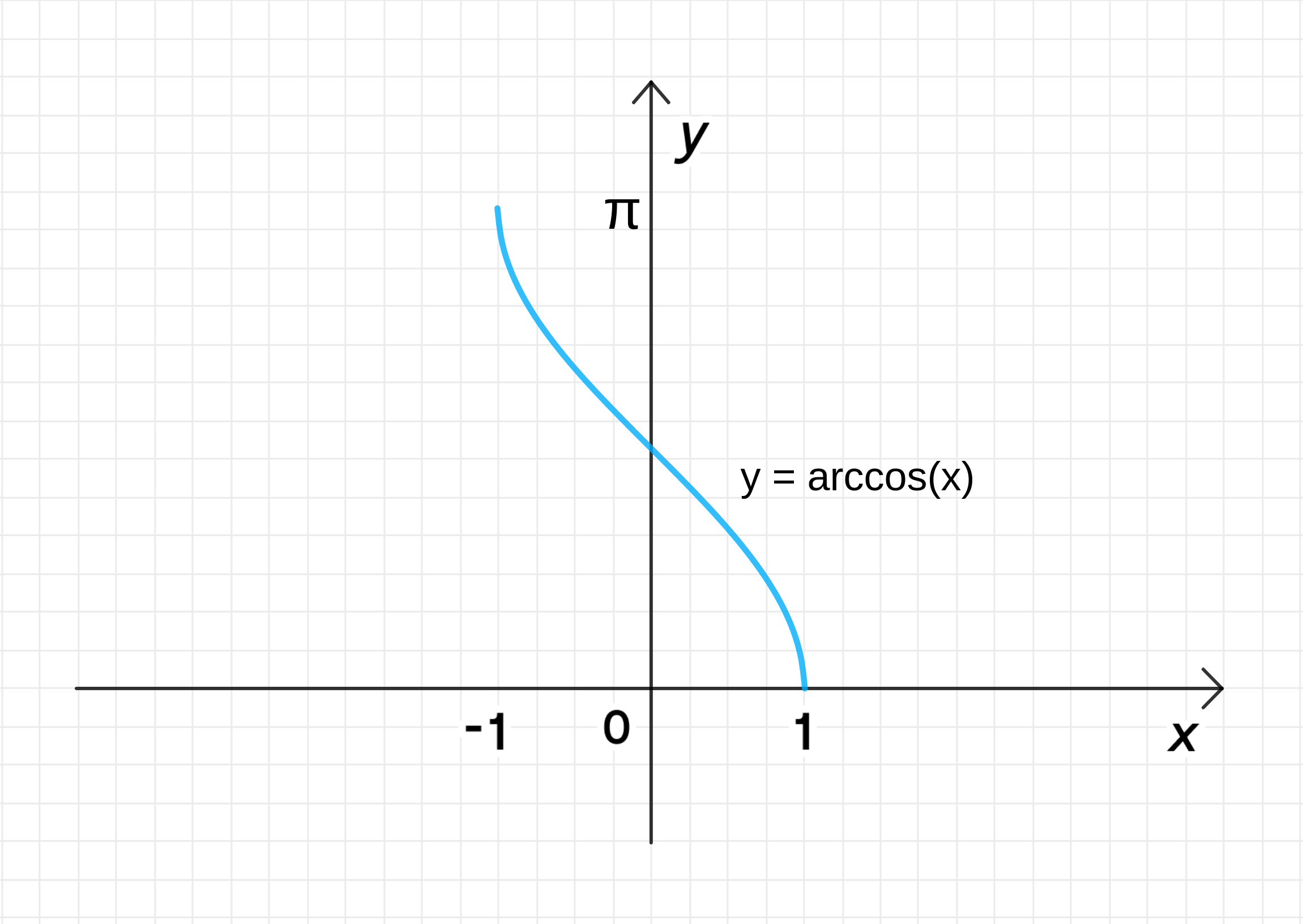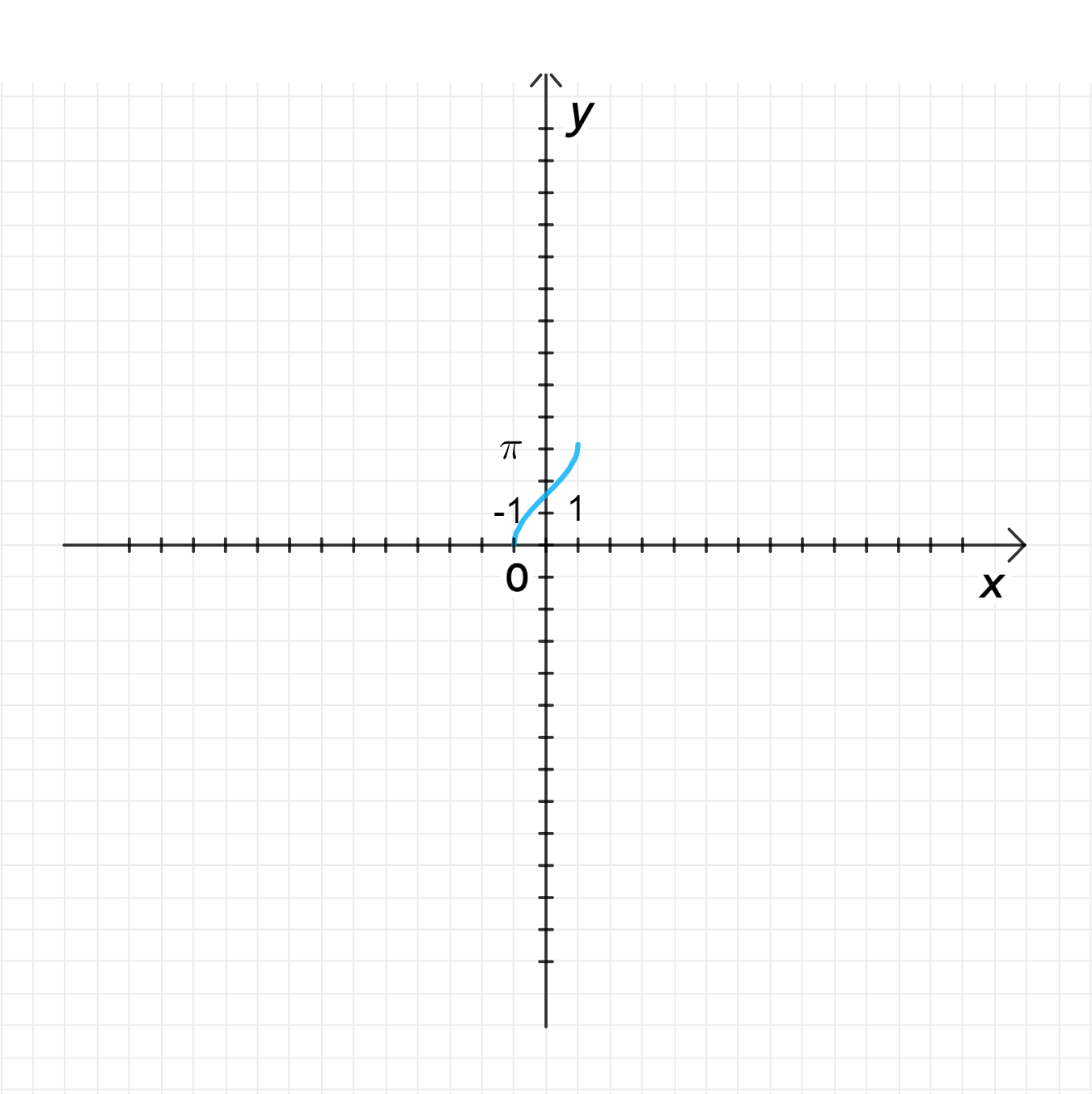ГДЗ по Алгебре 10 Класс Номер 21.25 Профильный Уровень Мордкович — Подробные Ответы

Постройте график функции:

а) у = arccosх

б) у = arccos(-x);

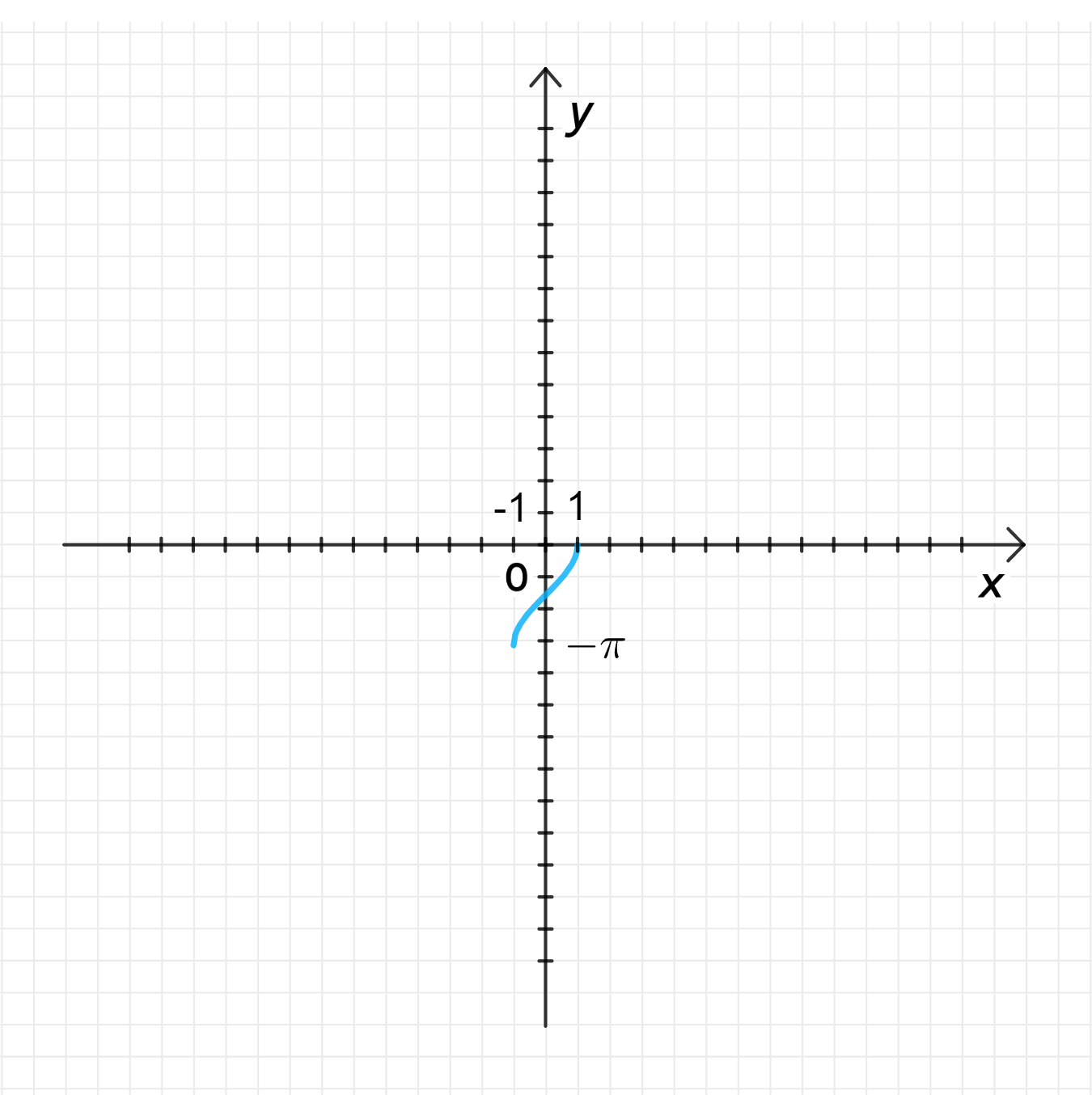
в) у = -arccosx;

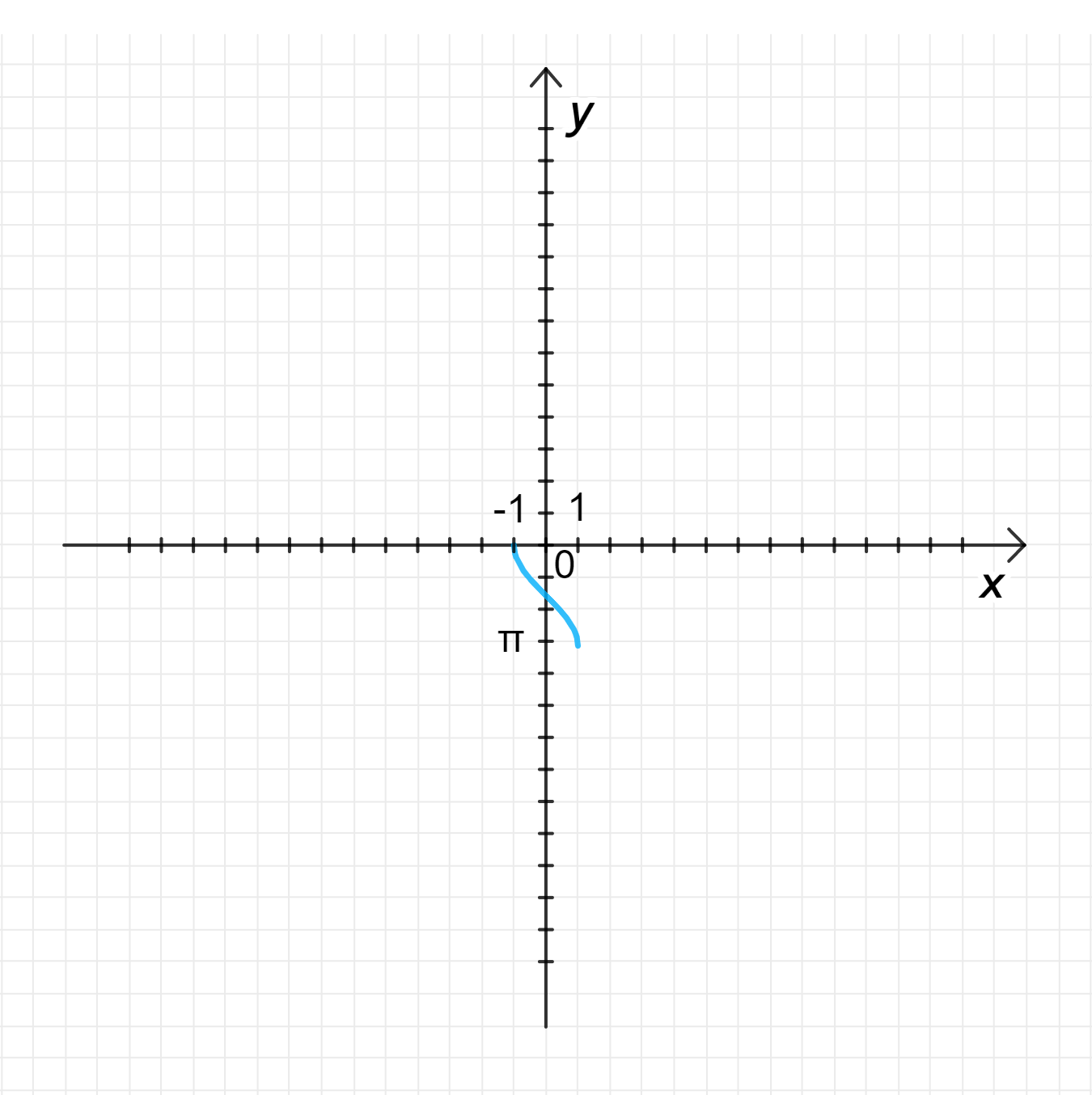
г) у = -arccos(-x).

а) $y = \arccos x$;

Построим график функции $y = \cos x$ на отрезке $[0; \pi]$;

Отразим его относительно прямой $y = x$:

б) $y = \arccos(-x)$;

Построим график функции $y = \arccos x$;

Отразим его относительно оси ординат:

в) $y = -\arccos x$;

Построим график функции $y = \arccos x$;

Отразим его относительно оси абсцисс:

г) $y = -\arccos(-x)$;

Построим график функции $y = \arccos x$;

Отразим его относительно оси ординат;

Отразим его относительно оси абсцисс:

Для начала, напомним, что функция $y = \arccos x$ является обратной к функции $y = \cos x$. Она определена на интервале $x \in [-1, 1]$ и принимает значения в интервале $[0, \pi]$. График функции $y = \arccos x$ на этом интервале будет выглядеть как спадная кривая, которая начинается от $y = 0$ при $x = 1$ и заканчивается в $y = \pi$ при $x = -1$.

а) $y = \arccos x$

Построение графика функции $y = \cos x$ на отрезке $[0; \pi]$:

Функция $y = \cos x$ — это стандартная косинусоидальная функция, но ограниченная на интервале $[0, \pi]$. График функции $y = \cos x$ на этом интервале начинается от $y = 1$ при $x = 0$ и убывает до $y = -1$ при $x = \pi$. График будет выглядеть как убывающая кривая от верхней точки до нижней точки.

Отражение графика функции относительно прямой $y = x$:

Отражение графика функции относительно прямой $y = x$ означает, что мы меняем местами оси абсцисс и ординат. То есть если точка на графике функции $y = \cos x$ имеет координаты $(x, y)$, то после отражения она будет находиться в точке $(y, x)$.

Таким образом, мы получаем график функции $y = \arccos x$. Он будет выглядеть как функция, убывающая от $y = \pi$ при $x = -1$ до $y = 0$ при $x = 1$. Это классическая форма графика функции арккосинуса.

б) $y = \arccos(-x)$

Построение графика функции $y = \arccos x$:

График функции $y = \arccos x$ уже был построен выше. Эта функция имеет значения в интервале $[0; \pi]$ для $x \in [-1; 1]$ и убывает.

Отражение графика функции относительно оси ординат:

Отражение графика функции относительно оси ординат означает, что мы заменяем $x$ на $-x$. Это преобразование не изменяет значения функции, поскольку $\arccos(-x)$ равно $\arccos x$ с изменением знака аргумента. Поскольку арккосинус — это четная функция (из-за симметрии косинуса), график функции $y = \arccos(-x)$ будет зеркально симметричен графику функции $y = \arccos x$ относительно оси ординат.

Итак, график функции $y = \arccos(-x)$ будет тем же, что и для $y = \arccos x$, но с изменением направления на оси абсцисс (от $x = -1$ до $x = 1$).

в) $y = -\arccos x$

Построение графика функции $y = \arccos x$:

Как мы уже обсуждали, график функции $y = \arccos x$ убывает от $y = 0$ при $x = 1$ до $y = \pi$ при $x = -1$.

Отражение графика функции относительно оси абсцисс:

Отражение графика относительно оси абсцисс означает, что мы меняем знак значения функции. То есть, если для некоторого $x$ график функции $y = \arccos x$ имеет значение $y$, то после отражения это значение будет $-y$.

Таким образом, график функции $y = -\arccos x$ будет аналогичен графику функции $y = \arccos x$, но с инверсией по оси $y$. График будет расти от $y = -\pi$ при $x = -1$ до $y = 0$ при $x = 1$.

г) $y = -\arccos(-x)$

Построение графика функции $y = \arccos x$:

Как уже обсуждалось, функция $y = \arccos x$ убывает от $y = 0$ при $x = 1$ до $y = \pi$ при $x = -1$.

Отражение графика функции относительно оси ординат:

Как мы уже говорили, $y = \arccos(-x)$ — это отражение функции $y = \arccos x$ относительно оси ординат. График функции будет симметричен относительно оси $y$.

Отражение графика относительно оси абсцисс:

Теперь мы отражаем график относительно оси абсцисс, то есть меняем знак функции. Получаем график, который убывает от $y = -\pi$ при $x = -1$ до $y = 0$ при $x = 1$.

Таким образом, график функции $y = -\arccos(-x)$ будет иметь тот же вид, что и для $y = \arccos x$, но отраженный сначала относительно оси ординат, а затем относительно оси абсцисс.