ГДЗ по Алгебре 10 Класс Номер 21.26 Профильный Уровень Мордкович — Подробные Ответы

Постройте и прочитайте график функции:

а) $y = \arccos(x-1) — \frac{\pi}{2}$;

б) $\arccos(x+2) + \frac{\pi}{3}$

а) $y = \arccos(x-1) — \frac{\pi}{2}$;

Построим график функции $y = \arccos x$;

Переместим его на 1 единицу вправо вдоль оси абсцисс;

Переместим его на $\frac{\pi}{2}$ единиц вниз вдоль оси ординат:

• Область определения: $D(f) = [0; 2]$;
• Множество значений: $E(f) = \left[ -\frac{\pi}{2}; \frac{\pi}{2} \right]$;
• Функция убывает;
• $f(x) > 0$ на $[0; 1)$;
• $f(x) < 0$ на $(1; 2]$;
• Функция ни четная, ни нечетная;

б) $\arccos(x+2) + \frac{\pi}{3}$;

Построим график функции $y = \arccos x$;

Переместим его на 2 единицы влево вдоль оси абсцисс;

Переместим его на $\frac{\pi}{3}$ единиц вверх вдоль оси ординат:

• Область определения: $D(f) = [-3; -1]$;
• Множество значений: $E(f) = \left[ \frac{\pi}{3}; \frac{4\pi}{3} \right]$;
• Функция убывает;
• $f(x) > 0$ на $[-3; -1]$;
• Функция ни четная, ни нечетная

а) $y = \arccos(x-1) — \frac{\pi}{2}$

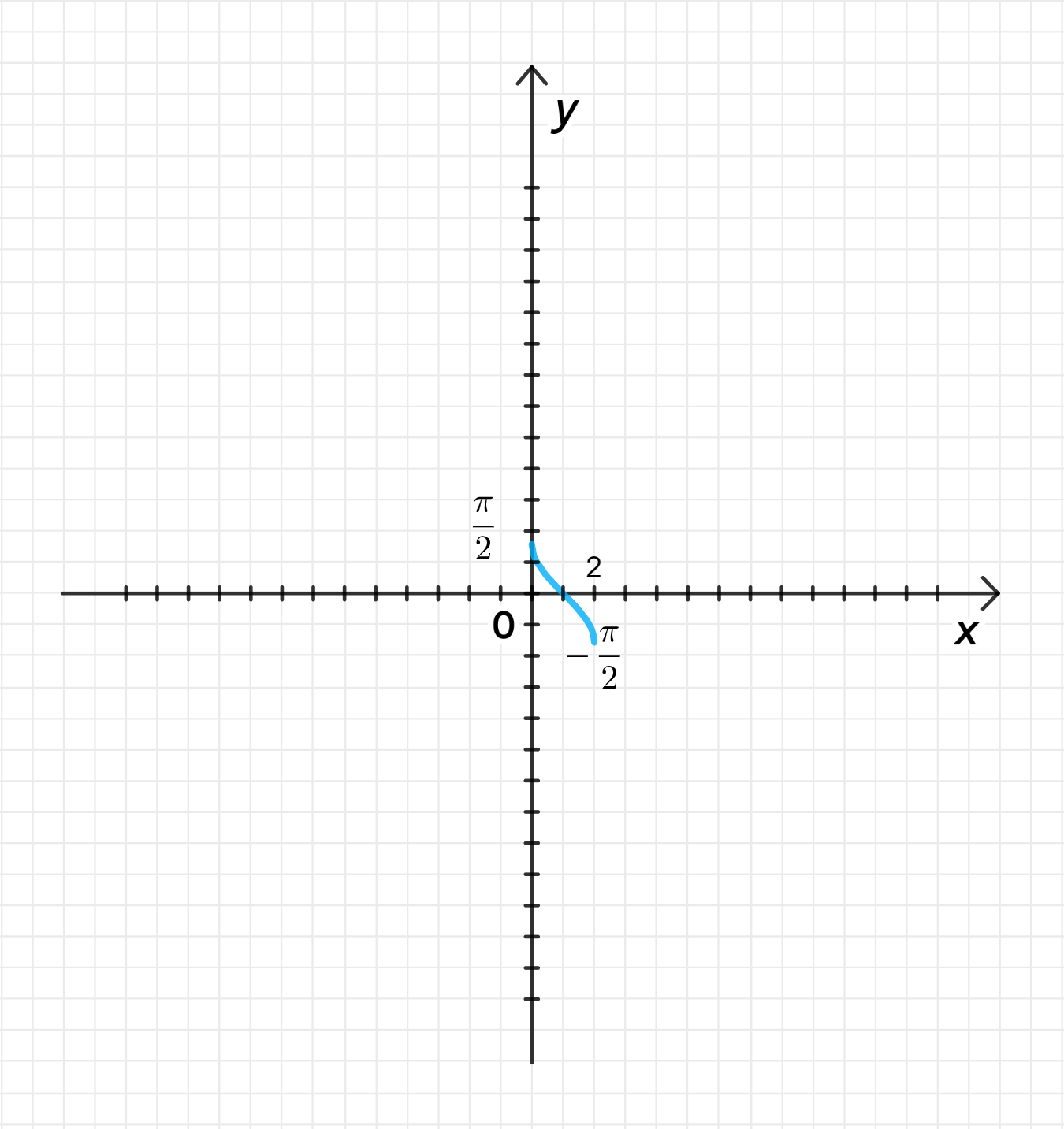
Построение графика функции $y = \arccos x$:

Функция $y = \arccos x$ является обратной к функции косинуса на интервале $[0, \pi]$. График функции $y = \arccos x$ на интервале $[-1, 1]$ убывает от $y = 0$ при $x = 1$ до $y = \pi$ при $x = -1$. Важные моменты:

• Область определения: $D(f) = [-1; 1]$.
• Множество значений: $E(f) = [0; \pi]$.
• Функция убывает.

Перемещение графика на 1 единицу вправо вдоль оси абсцисс:

Если сдвигать график функции $y = \arccos x$ на 1 единицу вправо, это означает, что $x$ заменяется на $x — 1$. То есть для функции $y = \arccos(x — 1)$ область определения будет изменена на интервал $[0; 2]$, так как $x — 1$ теперь лежит в интервале $[-1; 1]$.

Область определения после сдвига:

$$D(f) = [0; 2]$$

Перемещение графика на $\frac{\pi}{2}$ единиц вниз вдоль оси ординат:

Сдвиг функции $y = \arccos(x — 1)$ на $\frac{\pi}{2}$ вниз по оси $y$ означает, что к значению функции $y$ будет прибавляться $-\frac{\pi}{2}$. Это смещает весь график на $\frac{\pi}{2}$ вниз.

Множество значений после сдвига:

$$E(f)=[-\frac{\pi }{2};\frac{\pi }{2}]$$

Исследование свойств функции:

• Функция убывает: Как и для $y = \arccos x$, график функции $y = \arccos(x — 1) — \frac{\pi}{2}$ будет убывающим, так как мы не изменили этот аспект функции.
• Положительные и отрицательные значения функции:
  • $f(x) > 0$ на $[0; 1)$ — в этой области арккосинус остается положительным, но после сдвига вниз.
  • $f(x) < 0$ на $(1; 2]$ — в этой области функция становится отрицательной.

Область определения и множество значений:

• Область определения: $D(f) = [0; 2]$.
• Множество значений: $E(f) = \left[ -\frac{\pi}{2}; \frac{\pi}{2} \right]$.

$$\text{Ответ: } \, y \in [0; 2\pi]$$б) $y = \arccos(x+2) + \frac{\pi}{3}$

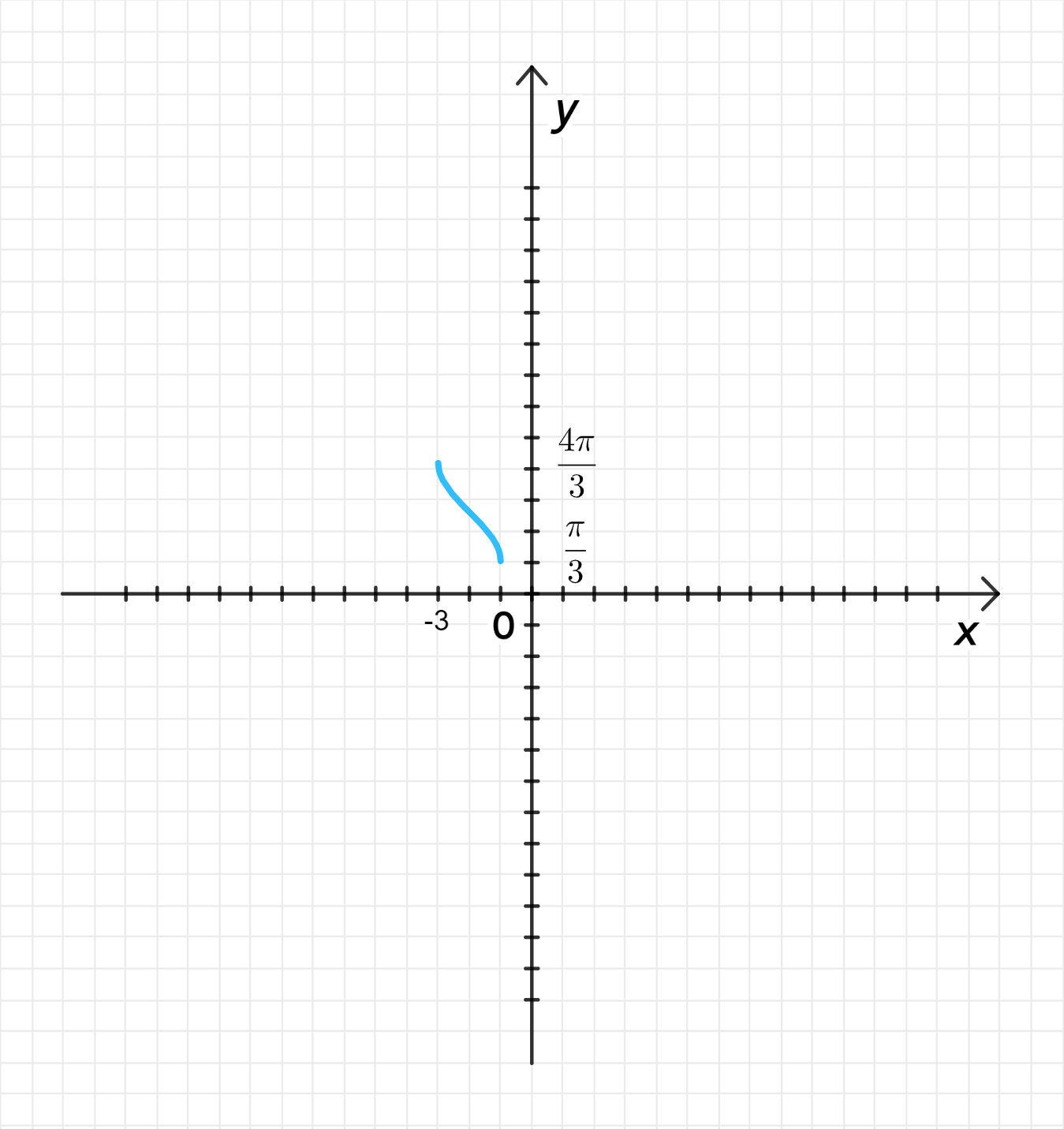
Построение графика функции $y = \arccos x$:

Мы знаем, что график функции $y = \arccos x$ убывает от $y = 0$ при $x = 1$ до $y = \pi$ при $x = -1$, и функция определена на интервале $[-1, 1]$.

Перемещение графика на 2 единицы влево вдоль оси абсцисс:

При сдвиге на 2 единицы влево, мы заменяем $x$ на $x + 2$. Это означает, что теперь область определения будет $[-3; -1]$, так как $x + 2$ теперь лежит в интервале $[-1; 1]$.

Область определения после сдвига:

$$D(f) = [-3; -1]$$

Перемещение графика на $\frac{\pi}{3}$ единиц вверх вдоль оси ординат:

Сдвиг функции $y = \arccos(x + 2)$ на $\frac{\pi}{3}$ вверх по оси $y$ означает, что к значению функции добавляется $\frac{\pi}{3}$, что сдвигает график вверх.

Множество значений после сдвига:

$$E(f) = \left[ \frac{\pi}{3}; \frac{4\pi}{3} \right]$$

Исследование свойств функции:

• Функция убывает: Так как $y = \arccos(x + 2)$ является убывающей функцией, то после сдвига график останется убывающим.
• Положительные и отрицательные значения функции:
  • $f(x) > 0$ на $[-3; -1]$ — поскольку арккосинус положителен на этом интервале, после сдвига он останется положительным.

Область определения и множество значений:

• Область определения: $D(f) = [-3; -1]$.
• Множество значений: $E(f) = \left[ \frac{\pi}{3}; \frac{4\pi}{3} \right]$.