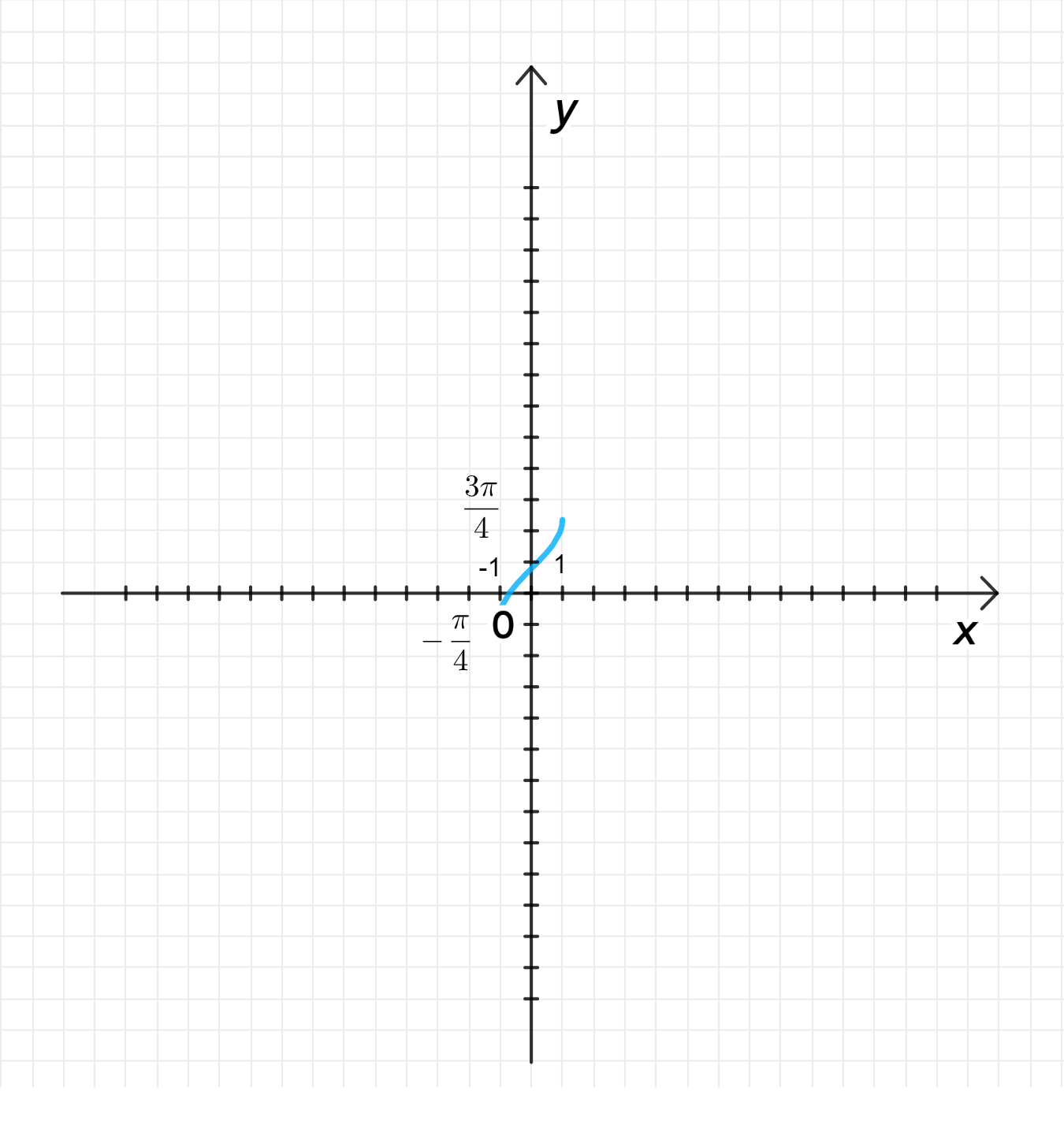Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 21.27 Профильный Уровень Мордкович — Подробные Ответы
Постройте и прочитайте график функции:
а)
б)
в)
г)
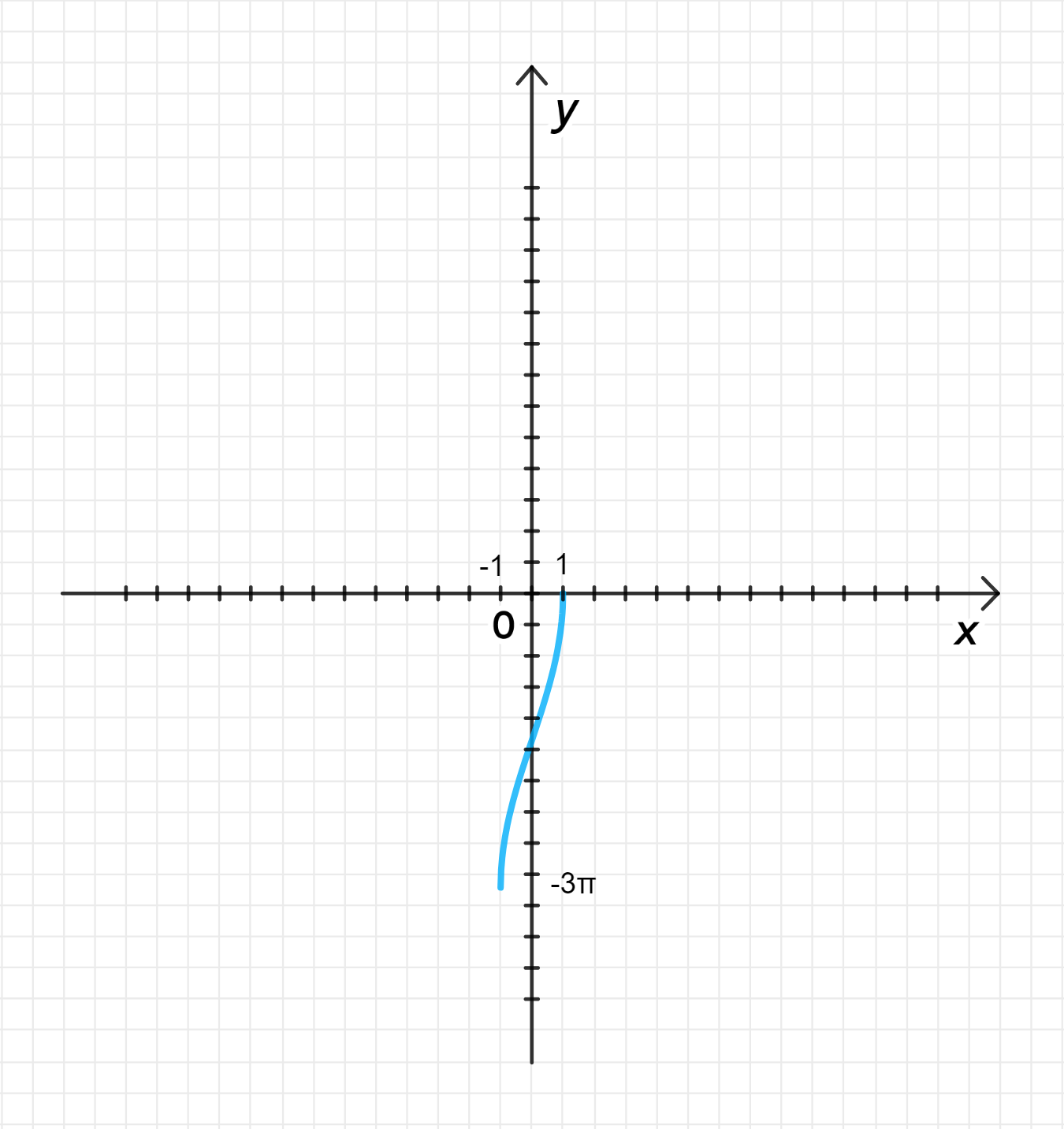
а)
Построим график функции ;
Отразим его относительно оси абсцисс;
Растянем его от оси с коэффициентом .
- Область определения: ;
- Множество значений: ;
- Функция возрастает;
- на ;
- Функция ни четная, ни нечетная;
б)
Построим график функции ;
Отразим его относительно оси абсцисс;
Переместим его на единиц вверх вдоль оси ординат.
- Область определения: ;
- Множество значений: ;
- Функция возрастает;
- на ;
- на ;
- Функция ни четная, ни нечетная;
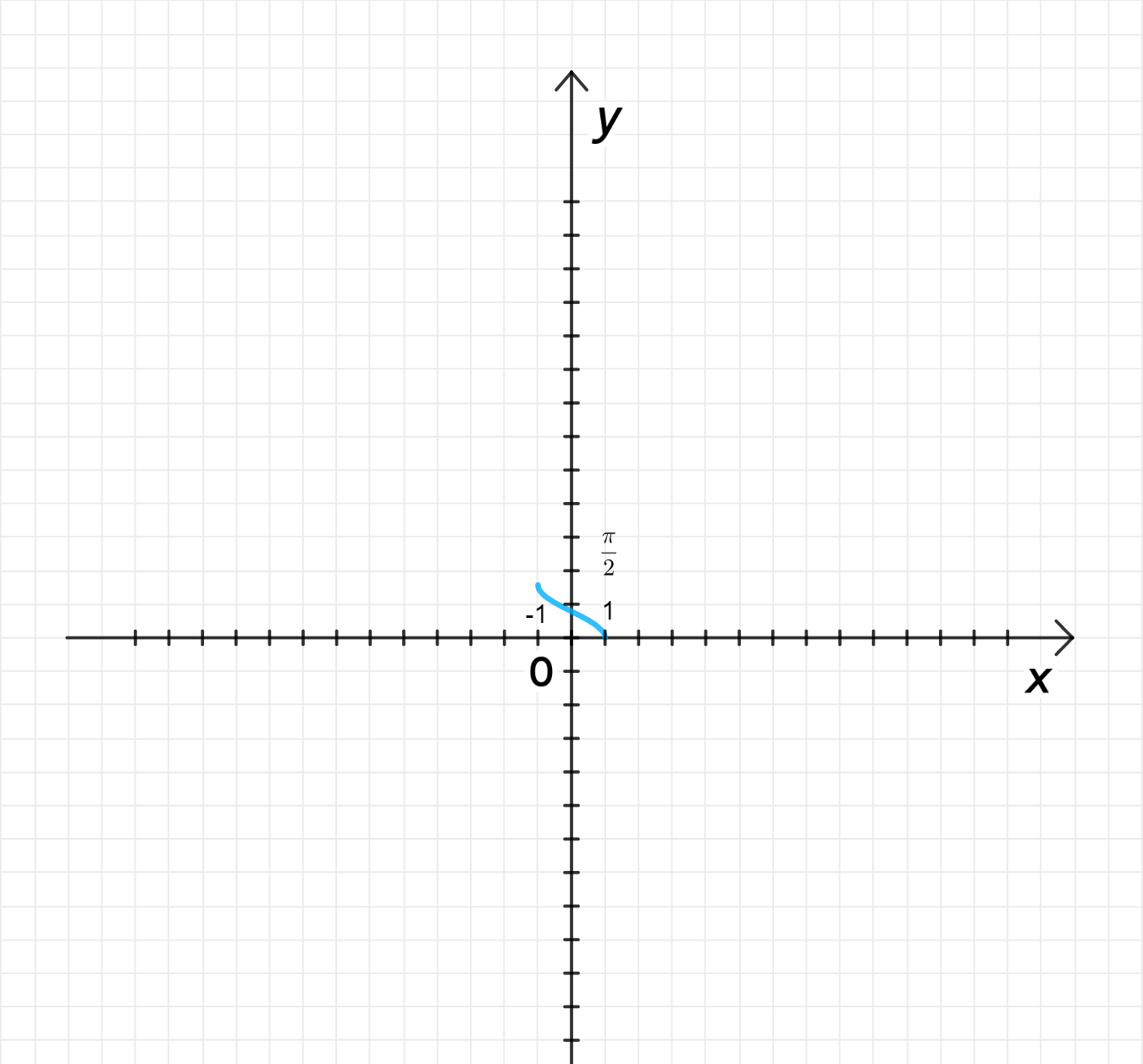
в)
Построим график функции ;
Сожмем его к оси с коэффициентом .
- Область определения: ;
- Множество значений: ;
- Функция убывает;
- на ;
- Функция ни четная, ни нечетная;
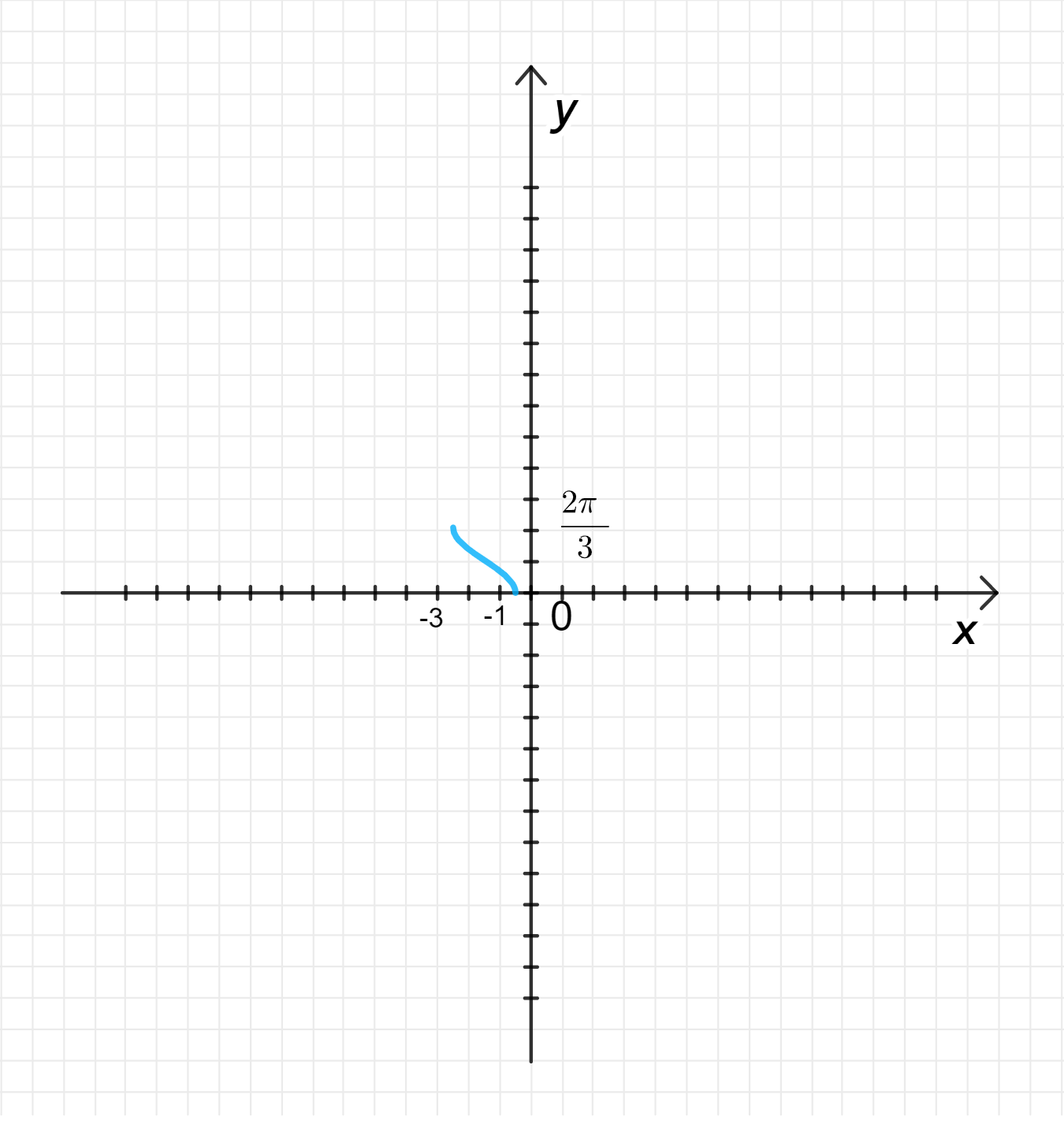
г)
Построим график функции ;
Переместим его на 1,5 единицы влево вдоль оси абсцисс;
Сожмем его к оси с коэффициентом .
- Область определения: ;
- Множество значений: ;
- Функция убывает;
- на ;
- Функция ни четная, ни нечетная
а)
Построение графика функции :
- График функции — это спадная кривая, которая начинается от при и доходит до при .
- Область определения: , так как функция определена на этом интервале.
- Множество значений: , так как значение арккосинуса всегда лежит в этом интервале.
Отражение относительно оси абсцисс:
- Отражение графика функции относительно оси абсцисс означает, что все значения функции меняют знак, но форма графика остается неизменной.
- После отражения , график функции будет тем же, но теперь убывающим (от до ).
Растяжение вдоль оси с коэффициентом :
- Растяжение функции с коэффициентом 3 по оси означает, что значения функции увеличиваются в 3 раза, что сжимает график по оси и растягивает его вдоль оси .
- Умножение на приводит к тому, что график будет растянут и инвертирован (от до , но с более крутым наклоном).
Исследование свойств функции:
- Область определения: .
- Множество значений: — поскольку максимальное значение функции равно , а после умножения на получаем интервал .
- Функция возрастает: Хотя сама функция убывает, умножение на делает её возрастающей.
- Знаки функции:
- на интервале , так как функция принимает отрицательные значения на этом интервале.
б)
Построение графика функции :
- График функции убывает от при до при .
- Область определения: , поскольку арккосинус определён для в интервале .
- Множество значений: .
Отражение относительно оси абсцисс:
- Как и в предыдущем примере, отражение графика относительно оси абсцисс инвертирует значения функции. После этого график функции будет тем же, но с отрицательными значениями.
Перемещение на единиц вверх:
- Перемещение графика на единиц вверх по оси ординат добавляет константу к каждому значению функции.
- Множество значений после сдвига будет:
Так как исходная функция имела диапазон значений , и добавление смещает его вверх.
Исследование свойств функции:
- Область определения: .
- Множество значений: .
- Функция возрастает: Из-за того, что убывает, а мы вычитаем это из , функция будет возрастать.
- Знаки функции:
- на интервале ,
- на .
в)
Построение графика функции :
- График функции убывает от при до при .
- Область определения: .
- Множество значений: .
Сжатие графика относительно оси с коэффициентом :
- Сжатие графика на оси с коэффициентом 2 означает, что график будет «плоским», и значения функции будут в 2 раза меньше.
- Результирующее множество значений будет , так как максимальное значение функции .
Исследование свойств функции:
- Область определения: .
- Множество значений: .
- Функция убывает: Поскольку функция убывает, сжатие графика не изменит её монотонности.
- Знак функции: на интервале .
г)
Построение графика функции :
- График функции убывает от при до при .
- Область определения: .
Перемещение графика на 1,5 единицы влево вдоль оси абсцисс:
- Перемещение функции на 1,5 единицы влево изменяет область определения. Для область определения будет , так как теперь лежит в интервале .
Сжатие графика относительно оси с коэффициентом :
- Сжатие функции относительно оси с коэффициентом 1,5 означает, что значения функции будут уменьшены на 1,5, и график станет более плоским.
- Множество значений после сжатия: .
Исследование свойств функции:
- Область определения: .
- Множество значений: .
- Функция убывает: Функция убывает, а её сжатие не изменяет монотонность.
- Знак функции: на интервале .