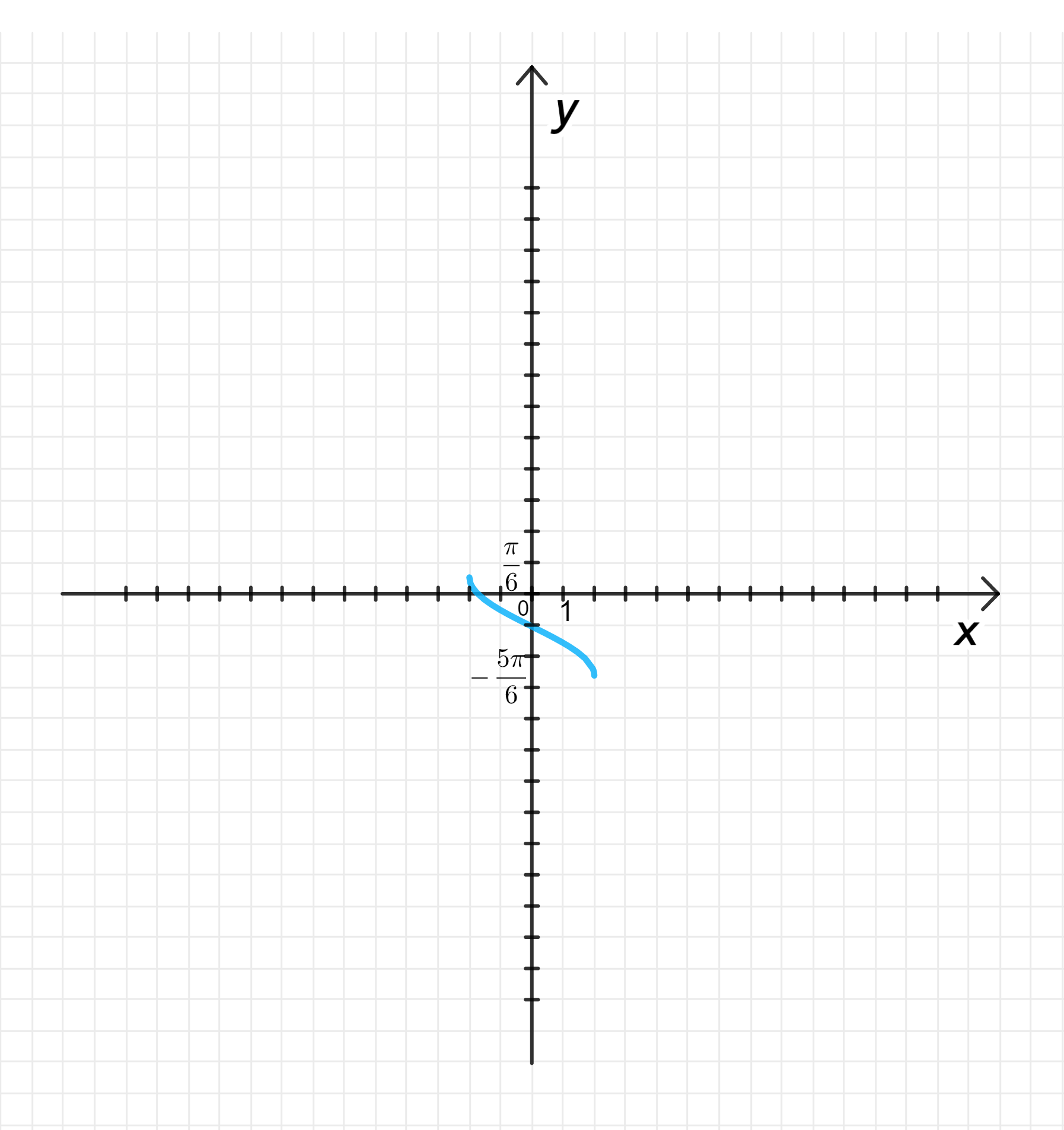Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 21.28 Профильный Уровень Мордкович — Подробные Ответы
Постройте и прочитайте график функции:
а) ;
б) ;
в) ;
г)
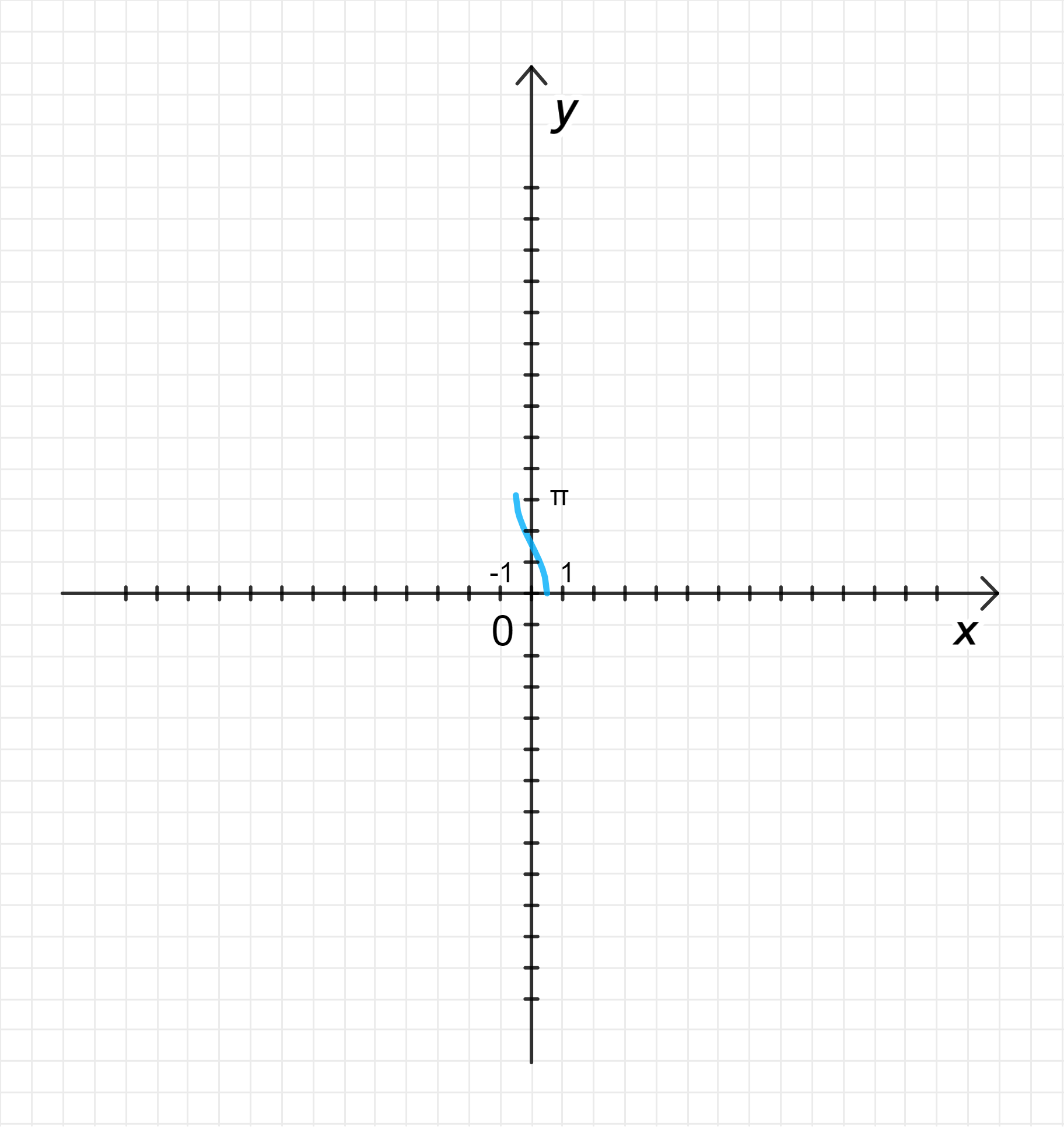
а) ;
Построим график функции ;
Сожмем его к оси с коэффициентом :
- Область определения: ;
- Множество значений: ;
- Функция убывает;
- на ;
- Функция ни четная, ни нечетная;
б) ;
Построим график функции ;
Растянем его от оси с коэффициентом ;
Переместим его на единиц вниз вдоль оси ординат:
- Область определения: ;
- Множество значений: ;
- Функция убывает;
- на ;
- на ;
- Функция ни четная, ни нечетная;
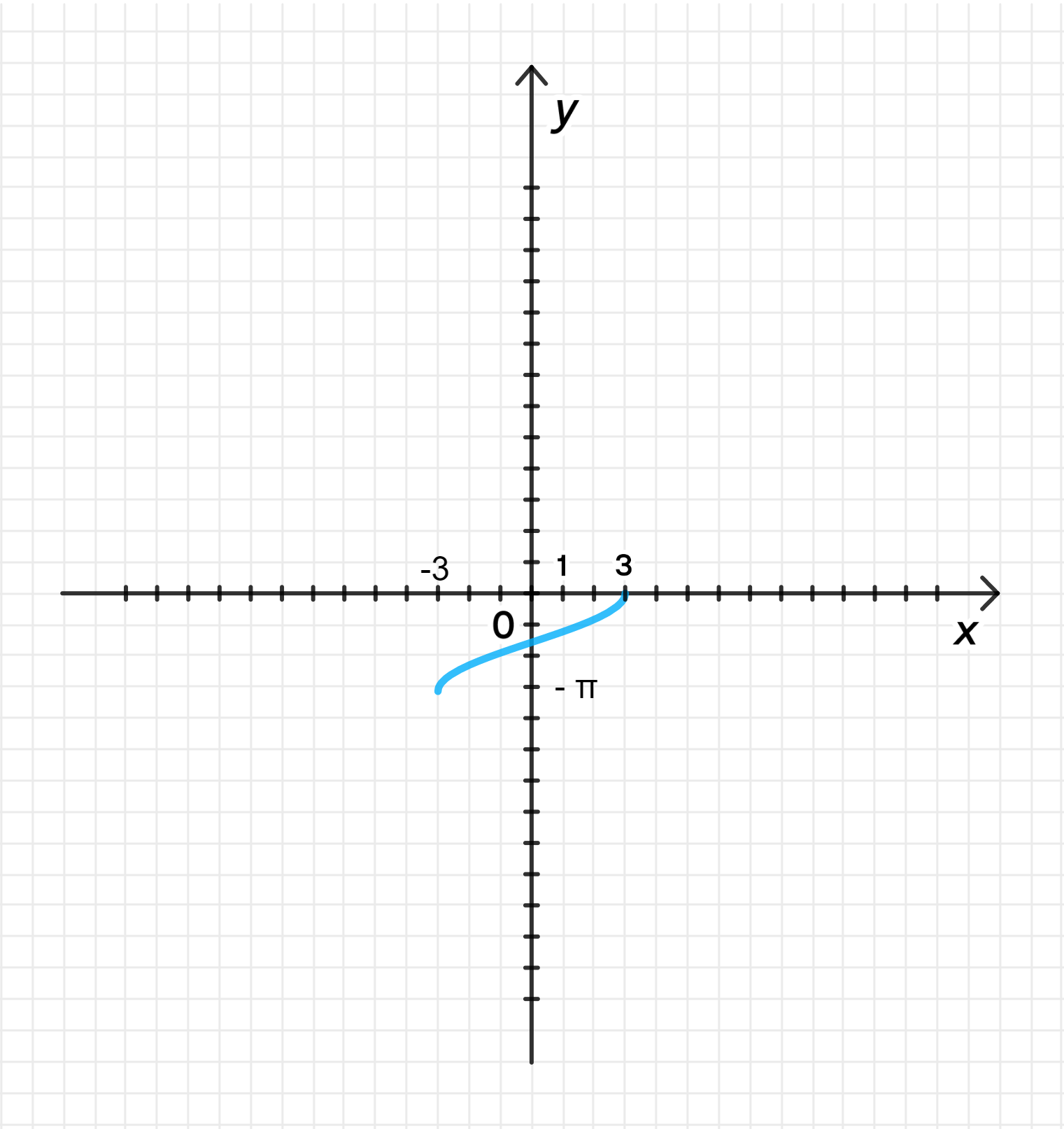
в) ;
Построим график функции ;
Растянем его от оси с коэффициентом ;
Отразим его относительно оси абсцисс:
- Область определения: ;
- Множество значений: ;
- Функция возрастает;
- на ;
- Функция ни четная, ни нечетная;
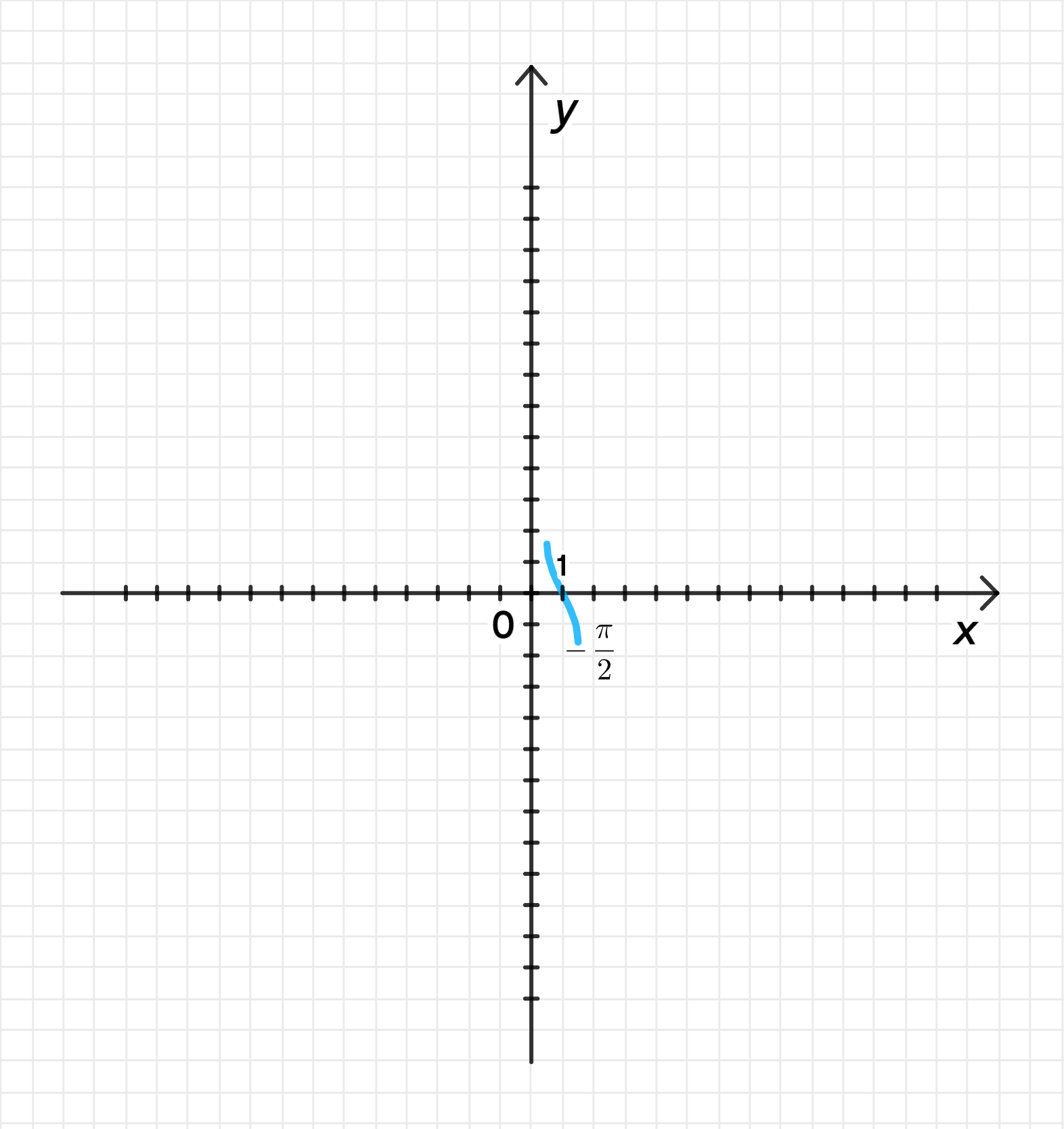
г) ;
Построим график функции ;
Сожмем его к оси с коэффициентом ;
Переместим его на 1 единицу вправо вдоль оси абсцисс;
Переместим его на единиц вниз вдоль оси ординат:
- Область определения: ;
- Множество значений: ;
- Функция убывает;
- на ;
- на ;
- Функция ни четная, ни нечетная
а)
Построение графика функции :
Функция — это обратная к функции косинуса на интервале , где:
- Область определения: , так как арккосинус определён для .
- Множество значений: , так как значение функции лежит в этом интервале.
- График функции убывает, начиная от при и заканчивая при .
Сжатие графика относительно оси с коэффициентом :
Сжатие функции по оси с коэффициентом означает, что значения функции будут уменьшены в два раза, а график будет сжаться по вертикали. То есть для каждого значения графика мы умножаем его на , что приводит к уменьшению диапазона значений функции.
- Множество значений после сжатия: останется прежним, поскольку сжатие происходит по вертикали, но не меняет сам диапазон.
Область определения функции:
При , область определения функции сужается, так как теперь должно лежать в интервале . Следовательно:
Разделим на 2:
Область определения будет:
Исследование свойств функции:
- Функция убывает: Функция продолжает оставаться убывающей, так как преобразования не меняют этого свойства для арккосинуса.
- Знак функции: Функция будет положительной на интервале , так как всегда положителен для .
б)
Построение графика функции :
Начинаем с построения графика функции , как это было сделано в предыдущем примере. График убывает от при до при .
Растяжение графика относительно оси с коэффициентом :
Растяжение графика относительно оси с коэффициентом увеличивает значения функции, что делает график более крутым. Для каждого значения графика значения будут увеличиваться в 2 раза. Это сдвигает диапазон значений функции.
- Множество значений после растяжения: будет изменено на , так как максимальное значение арккосинуса после растяжения станет .
Перемещение на единиц вниз вдоль оси ординат:
После растяжения графика мы перемещаем его на единиц вниз. Это смещает весь график вниз, и теперь область значений будет ограничена интервалом:
Исследование свойств функции:
- Функция убывает: Сдвиг и растяжение не изменяют монотонности функции.
- Знак функции:
- на интервале ,
- на .
в)
Построение графика функции :
Мы начинаем с того же графика функции , который убывает от при до при .
Растяжение графика относительно оси с коэффициентом :
Растяжение с коэффициентом увеличивает значения функции в 3 раза. Таким образом, максимальное значение арккосинуса после растяжения станет , и диапазон значений функции изменится.
Отражение относительно оси абсцисс:
Отражение относительно оси абсцисс меняет знак всех значений функции. Теперь функция будет возрастать, так как мы инвертируем график, а не растягиваем его вверх.
- Множество значений функции после отражения: , так как график функции стал положительным и убывающим на интервале .
Исследование свойств функции:
- Функция возрастает: После отражения относительно оси абсцисс график функции будет возрастать.
- Знак функции:
- на интервале .
г)
Построение графика функции :
График функции построен как спадная кривая от при до при .
Сжатие графика относительно оси с коэффициентом :
Сжатие графика с коэффициентом изменяет диапазон значений на на .
Перемещение на 1 единицу вправо вдоль оси абсцисс:
Сдвиг на 1 единицу вправо изменяет область определения функции на , так как теперь лежит в интервале .
Перемещение на единиц вниз вдоль оси ординат:
Сдвиг вниз на единиц смещает все значения функции на вниз. Множество значений будет теперь:
Исследование свойств функции:
- Функция убывает: Сдвиг и растяжение не изменяют убывающую монотонность функции.
- Знак функции:
- на интервале ,
- на интервале .