ГДЗ по Алгебре 10 Класс Номер 21.29 Профильный Уровень Мордкович — Подробные Ответы Задача
Постройте и прочитайте график функции:
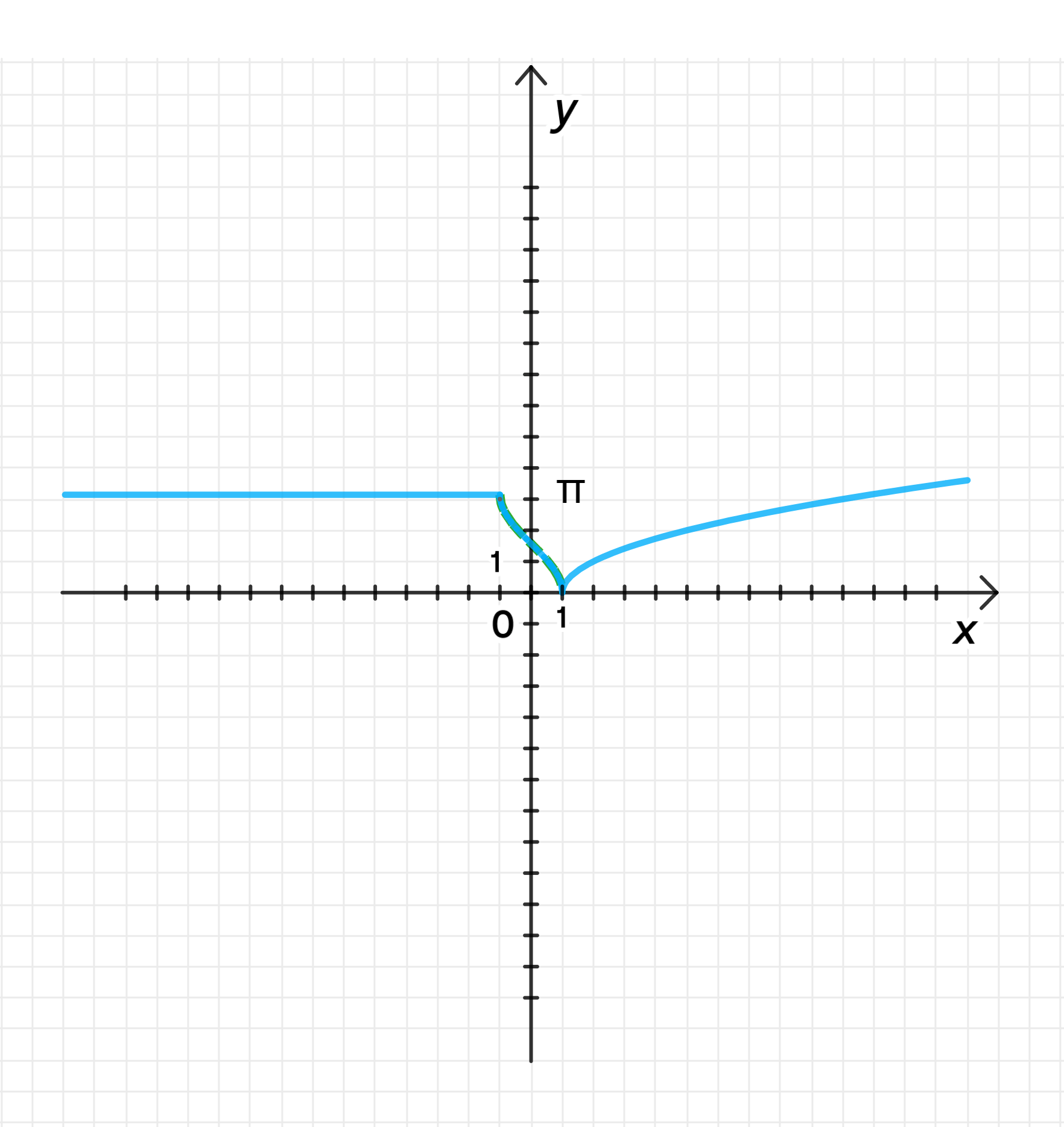
а) y = { π , если x < − 1 arccos x , если − 1 ≤ x ≤ 1 x − 1 , если x > 1
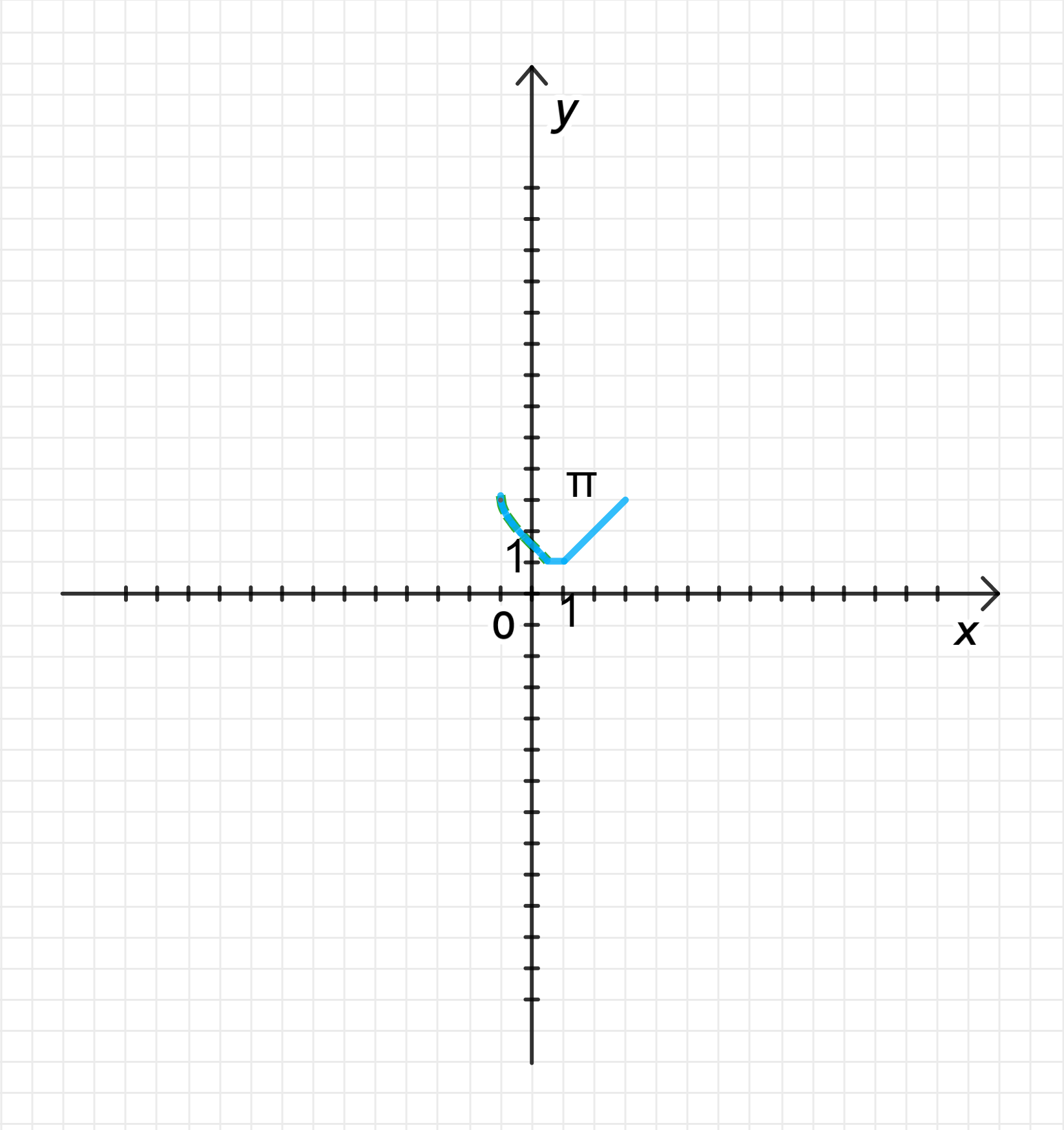
б) y = { arccos x , если − 1 ≤ x ≤ 0.5 π 3 , если 0.5 < x ≤ π 3 x , если π 3 < x ≤ 3
Краткий ответ:
а) y = { π , если x < − 1 arccos x , если − 1 ≤ x ≤ 1 x − 1 , если x > 1 y = \begin{cases} \pi, & \text{если } x < -1 \\ \arccos x, & \text{если } -1 \leq x \leq 1 \\ \sqrt{x-1}, & \text{если } x > 1 \end{cases}
y = π y = \pi
y = arccos x y = \arccos x
y = x − 1 y = \sqrt{x-1} x 0 = 1 x_0 = 1 y 0 = 0 y_0 = 0
Графики функций:
Свойства функции:
Область определения: D ( f ) = ( − ∞ ; + ∞ ) D(f) = (-\infty; +\infty) Множество значений: E ( f ) = [ 0 ; + ∞ ) E(f) = [0; +\infty) Возрастает на [ 1 ; + ∞ ) [1; +\infty) Убывает на [ − 1 ; 1 ] [-1; 1] Постоянна на ( − ∞ ; − 1 ] (-\infty; -1] f ( x ) > 0 f(x) > 0 ( − ∞ ; 1 ) ∪ ( 1 ; + ∞ ) (-\infty; 1) \cup (1; +\infty) Функция ни четная, ни нечетная; Функция не является периодической; б) y = { arccos x , если − 1 ≤ x ≤ 0.5 π 3 , если 0.5 < x ≤ π 3 x , если π 3 < x ≤ 3 y = \begin{cases} \arccos x, & \text{если } -1 \leq x \leq 0.5 \\ \frac{\pi}{3}, & \text{если } 0.5 < x \leq \frac{\pi}{3} \\ x, & \text{если } \frac{\pi}{3} < x \leq 3 \end{cases}
y = arccos x y = \arccos x
x x − 1 -1 0.5 0.5 y y π \pi π 3 \frac{\pi}{3}
y = π 3 y = \frac{\pi}{3}
y = x y = x
x x π 3 \frac{\pi}{3} 2 2 y y π 3 \frac{\pi}{3} 2 2
Графики функций:
Свойства функции:
Область определения: D ( f ) = [ − 1 ; 3 ] D(f) = [-1; 3] Множество значений: E ( f ) = [ π 3 ; π ] E(f) = \left[ \frac{\pi}{3}; \pi \right] Возрастает на [ π 3 ; 3 ] \left[ \frac{\pi}{3}; 3 \right] Убывает на [ − 1 ; 0.5 ] [-1; 0.5] Постоянна на [ 0.5 ; π 3 ] \left[ 0.5; \frac{\pi}{3} \right] f ( x ) > 0 f(x) > 0 [ − 1 ; 3 ] [-1; 3] Функция ни четная, ни нечетная; Функция не является периодической Подробный ответ:
а)
Функция задана по частям:
y = { π , x < − 1 arccos x , − 1 ≤ x ≤ 1 x − 1 , x > 1 y = \begin{cases} \pi, & x < -1 \\ \arccos x, & -1 \leq x \leq 1 \\ \sqrt{x — 1}, & x > 1 \end{cases}
1. Анализ каждой части
1.1. y = π y = \pi x < − 1 x < -1
Это прямая , параллельная оси Ox, на высоте y = π y = \pi Значение постоянное для всех x < − 1 x < -1 1.2. y = arccos x y = \arccos x − 1 ≤ x ≤ 1 -1 \le x \le 1
Это обратная функция к cos x \cos x [ − 1 , 1 ] [-1, 1] Область определения: [ − 1 ; 1 ] [-1; 1] Множество значений: [ 0 ; π ] [0; \pi] Убывает: так как cos x \cos x [ 0 ; π ] [0; \pi] arccos x \arccos x [ − 1 ; 1 ] [-1; 1] Примеры:arccos ( − 1 ) = π \arccos(-1) = \pi arccos ( 0 ) = π 2 \arccos(0) = \frac{\pi}{2} arccos ( 1 ) = 0 \arccos(1) = 0 1.3. y = x − 1 y = \sqrt{x — 1} x > 1 x > 1
Это ветвь параболы , сдвинутая на 1 вправо. Определена для x > 1 x > 1 Значения:x = 1 ⇒ y = 0 x = 1 \Rightarrow y = 0 x = 2 ⇒ y = 1 x = 2 \Rightarrow y = 1 x = 5 ⇒ y = 2 x = 5 \Rightarrow y = 2 Возрастает, так как производная y ′ = 1 2 x − 1 > 0 y’ = \frac{1}{2\sqrt{x-1}} > 0 2. Сводная таблица значений
x x y y y y x < − 1 x < -1 π \pi π \pi − 1 -1 arccos ( − 1 ) \arccos(-1) π \pi 0 0 arccos ( 0 ) \arccos(0) π 2 \frac{\pi}{2} 1 1 arccos ( 1 ) \arccos(1) 0 0 2 2 2 − 1 \sqrt{2 — 1} 1 1 5 5 5 − 1 \sqrt{5 — 1} 2 2
3. График
4. Свойства функции
Свойство Ответ Область определения D ( f ) = ( − ∞ ; + ∞ ) D(f) = (-\infty; +\infty) Множество значений E ( f ) = [ 0 ; π ] E(f) = [0; \pi] Монотонность Возрастает на ( 1 ; + ∞ ) (1; +\infty) Убывает на [ − 1 ; 1 ] [-1; 1] Постоянна на ( − ∞ ; − 1 ) (-\infty; -1) Промежутки знакоположительности f ( x ) > 0 f(x) > 0 ( − ∞ ; 1 ) ∪ ( 1 ; + ∞ ) (-\infty; 1) \cup (1; +\infty) Четность Не чётная и не нечётная Периодичность Не является периодической
б)
Функция по частям:
y = { arccos x , − 1 ≤ x ≤ 0.5 π 3 , 0.5 < x ≤ π 3 x , π 3 < x ≤ 3 y = \begin{cases} \arccos x, & -1 \le x \le 0.5 \\ \frac{\pi}{3}, & 0.5 < x \le \frac{\pi}{3} \\ x, & \frac{\pi}{3} < x \le 3 \end{cases}
1. Анализ каждой части
1.1. y = arccos x y = \arccos x − 1 ≤ x ≤ 0.5 -1 \le x \le 0.5
Уже рассмотрели в пункте (а). Убывающая на этом интервале. Примеры:arccos ( − 1 ) = π \arccos(-1) = \pi arccos ( 0.5 ) = π 3 \arccos(0.5) = \frac{\pi}{3} 1.2. y = π 3 y = \frac{\pi}{3} 0.5 < x ≤ π 3 0.5 < x \le \frac{\pi}{3}
Постоянная функция. Горизонтальная линия от x = 0.5 x = 0.5 x = π 3 ≈ 1.047 x = \frac{\pi}{3} \approx 1.047 1.3. y = x y = x π 3 < x ≤ 3 \frac{\pi}{3} < x \le 3
Прямая линия через начало координат, но начинается от x = π 3 x = \frac{\pi}{3} Примеры:x = π 3 ⇒ y = π 3 x = \frac{\pi}{3} \Rightarrow y = \frac{\pi}{3} x = 2 ⇒ y = 2 x = 2 \Rightarrow y = 2 2. Сводная таблица значений
x x y y y y − 1 -1 arccos ( − 1 ) \arccos(-1) π \pi 0.5 0.5 arccos ( 0.5 ) \arccos(0.5) π 3 \frac{\pi}{3} 0.6 0.6 π 3 \frac{\pi}{3} π 3 \frac{\pi}{3} π 3 \frac{\pi}{3} x x π 3 \frac{\pi}{3} 2 2 x x 2 2 3 3 x x 3 3
3. График
x = 3
4. Свойства функции
Свойство Ответ Область определения D ( f ) = [ − 1 ; 3 ] D(f) = [-1; 3] Множество значений E ( f ) = [ π 3 ; π ] E(f) = \left[\frac{\pi}{3}; \pi \right] Монотонность Возрастает на ( π 3 ; 3 ] \left(\frac{\pi}{3}; 3\right] Убывает на [ − 1 ; 0.5 ] [-1; 0.5] Постоянна на ( 0.5 ; π 3 ] (0.5; \frac{\pi}{3}] Знак f ( x ) > 0 f(x) > 0 Четность Не чётная и не нечётная Периодичность Не периодическая