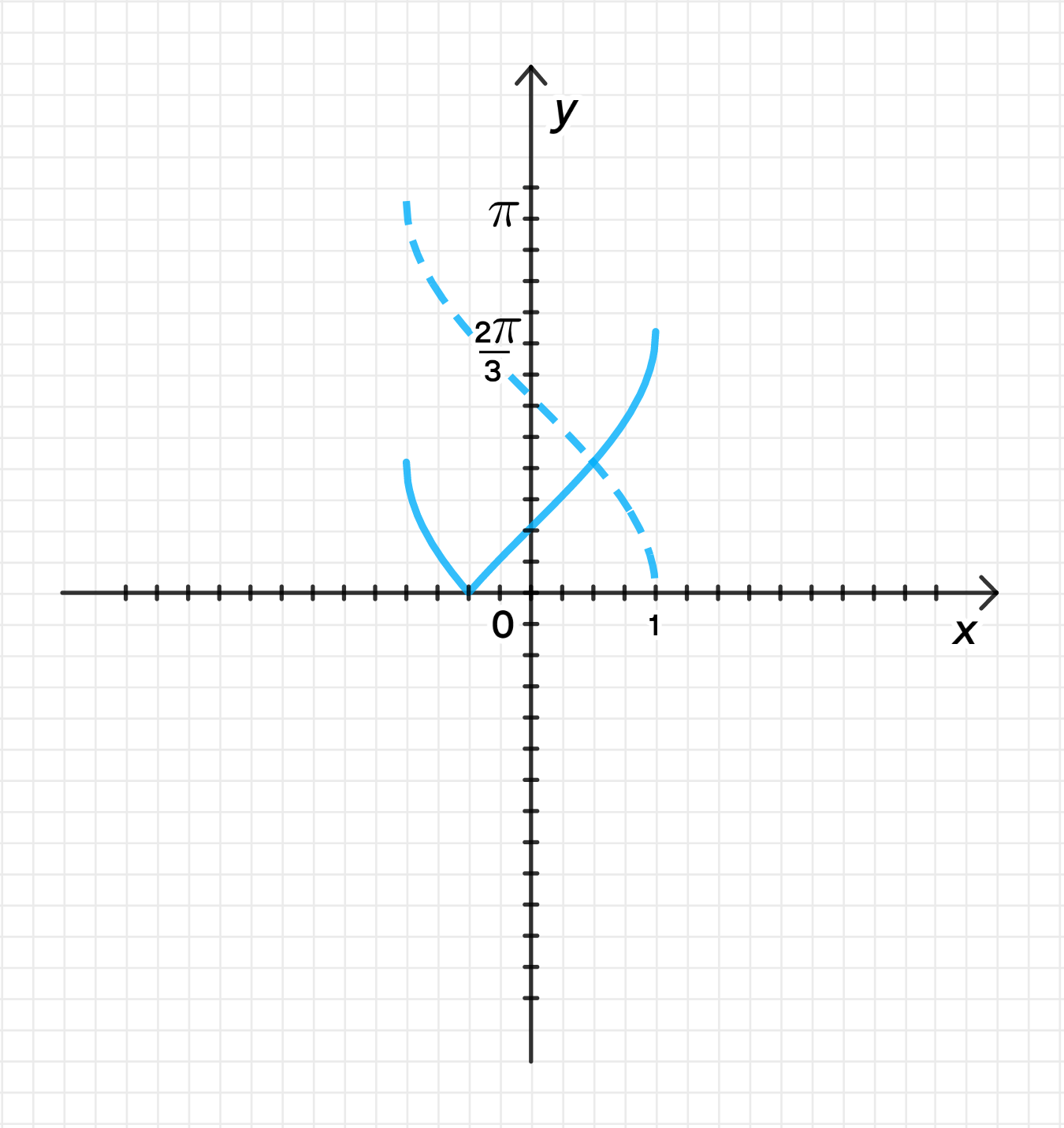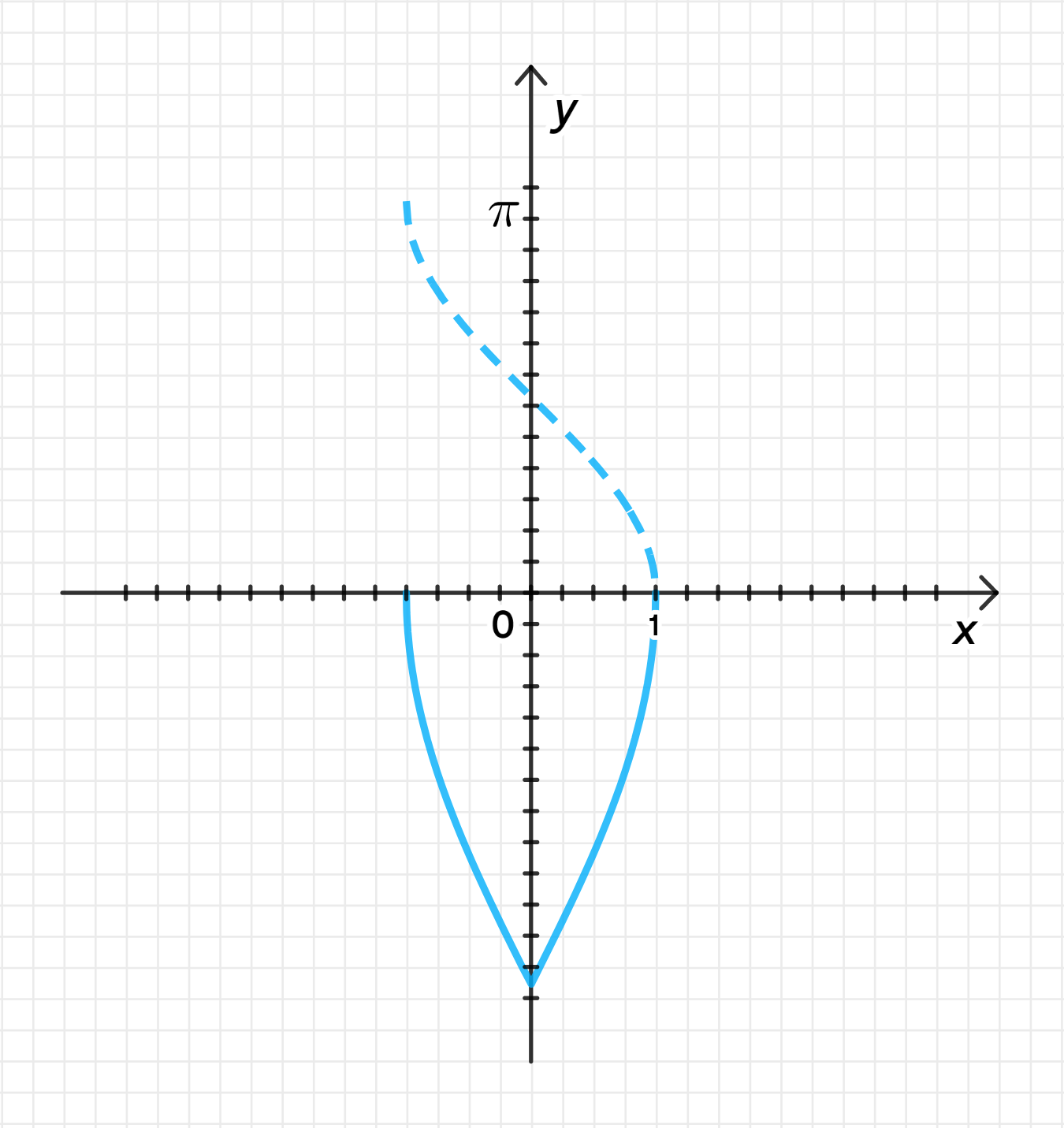ГДЗ по Алгебре 10 Класс Номер 21.30 Профильный Уровень Мордкович — Подробные Ответы

Постройте график функции:

а) $y = \left| \arccos x — \frac{2\pi}{3} \right|$;

б) $y = \arccos |x|$;

в) $y = -2 \arccos |x|$;

г) $y = \arccos |x — 2|$

а) $y = \left| \arccos x — \frac{2\pi}{3} \right|$;

Построим график функции $y = \arccos x$;

Переместим его на $\frac{2\pi}{3}$ единиц вниз вдоль оси ординат;

Отразим относительно оси $Ox$ часть графика, лежащую под ней:

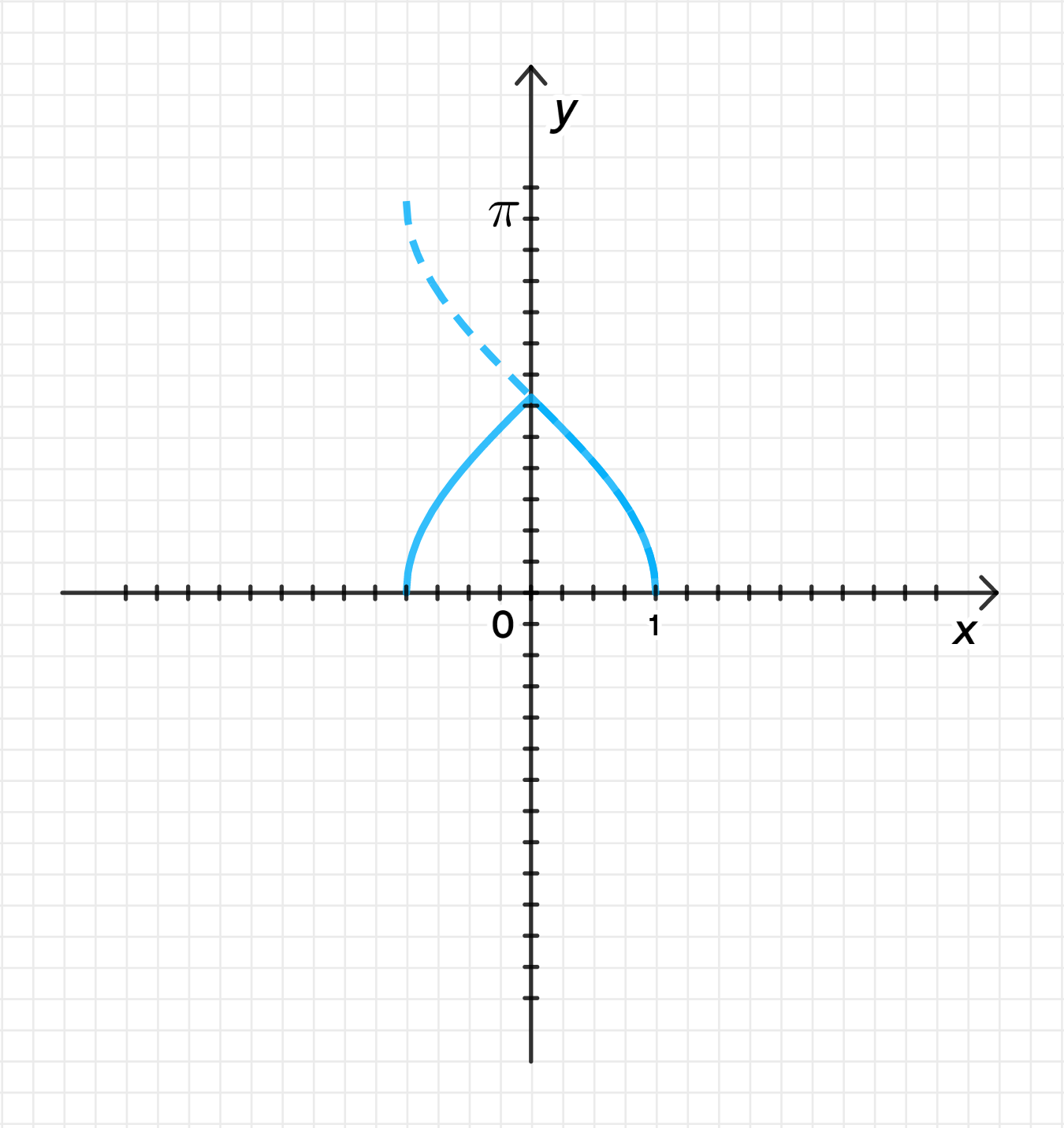
б) $y = \arccos |x|$;

Построим график функции $y = \arccos x$;

Уберем часть графика, лежащую слева от оси $Oy$;

Отразим относительно нее часть графика, лежащую справа:

в) $y = -2 \arccos |x|$;

Построим график функции $y = \arccos x$;

Уберем часть графика, лежащую слева от оси $Oy$;

Отразим относительно нее часть графика, лежащую справа;

Отразим график относительно оси $Ox$;

Растянем его от оси $Ox$ с коэффициентом $k = 2$:

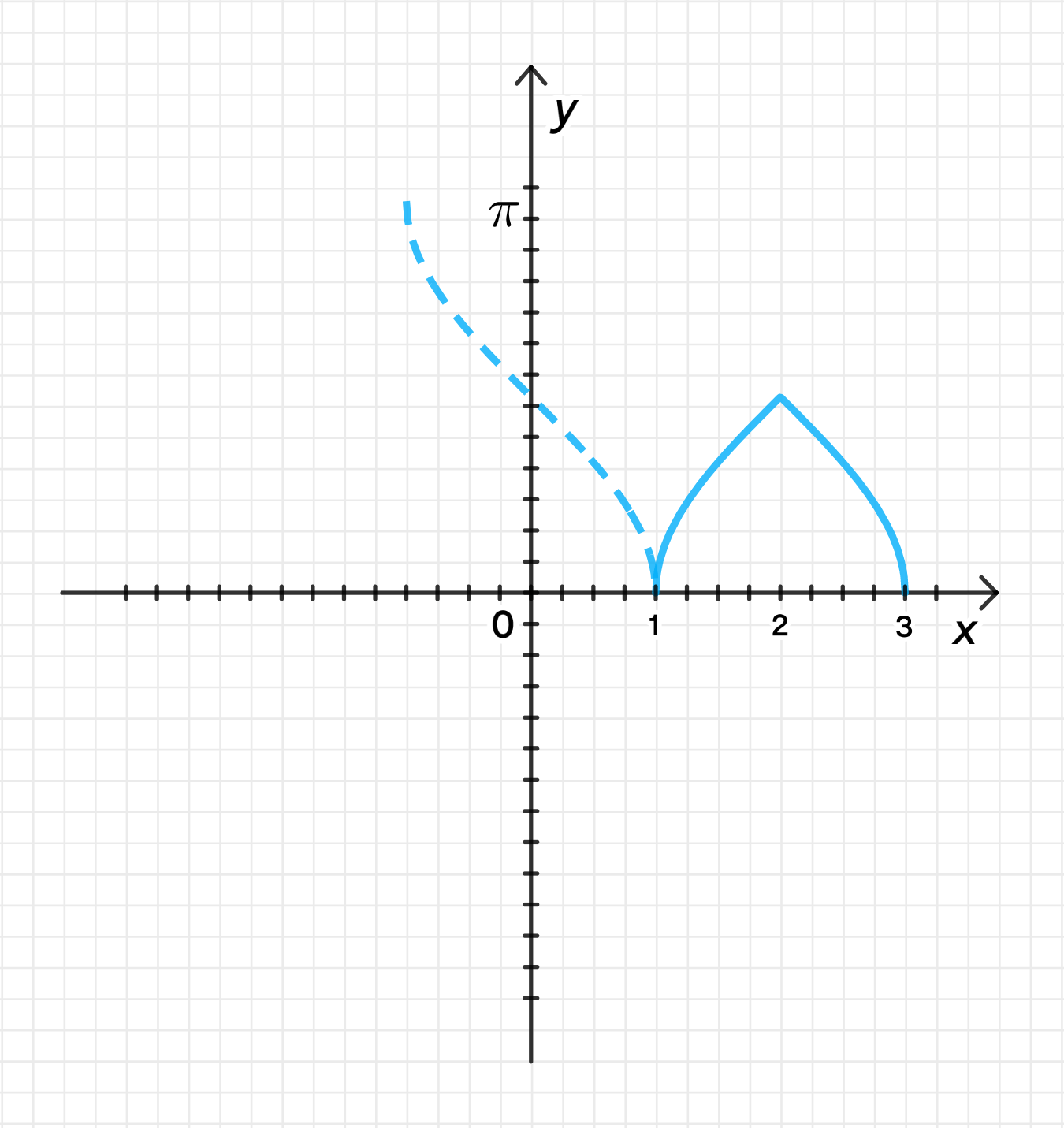
г) $y = \arccos |x — 2|$;

Построим график функции $y = \arccos x$;

Переместим его на 2 единицы вправо вдоль оси абсцисс;

Уберем часть графика, лежащую слева от прямой $x = 2$;

Отразим относительно нее часть графика, лежащую справа:

Базовая функция: $y = \arccos x$

Область определения: $x \in [-1, 1]$
Множество значений: $y \in [0, \pi]$
Краткое описание графика: убывающая кривая от точки $(-1, \pi)$ до точки $(1, 0)$.

а) $y = \left| \arccos x — \frac{2\pi}{3} \right|$

Шаг 1: Построим $y = \arccos x$

Это стандартный график, как описано выше.

Шаг 2: $y = \arccos x — \frac{2\pi}{3}$

Что происходит:
Мы сдвигаем график на $\frac{2\pi}{3}$ вниз по оси $y$.

Координаты точек изменяются:

• $(-1, \pi) \to (-1, \pi — \frac{2\pi}{3}) = (-1, \frac{\pi}{3})$
• $(1, 0) \to (1, -\frac{2\pi}{3})$

Теперь часть графика может оказаться ниже оси Ox.

Шаг 3: Применим модуль: $y = \left| \arccos x — \frac{2\pi}{3} \right|$

Что происходит:
Все отрицательные значения $y$ становятся положительными.
То есть часть графика, находящаяся ниже оси Ox, отражается вверх.

Пример:

• Точка $(1, -\frac{2\pi}{3}) \to (1, \frac{2\pi}{3})$

Итоговый график:

б) $y = \arccos |x|$

Шаг 1: Построим $y = \arccos x$

Убывающая кривая от $(-1, \pi)$ до $(1, 0)$

Шаг 2: Преобразование $|x|$

Что происходит:
Берём график для $x \ge 0$ (правая половина) и отражаем его влево (в область $x < 0$).

Итог:

• Удаляем левую часть графика (где $x < 0$)
• Отражаем правую часть (где $x \in [0, 1]$) относительно оси $Oy$

Итоговый график:

$x = \pm 1$

в) $y = -2 \arccos |x|$

Шаг 1: $y = \arccos x$ — стандартный график.

Шаг 2: $y = \arccos |x|$

Симметричный график, как в пункте б.
Определён на $x \in [-1, 1]$

Шаг 3: $y = -\arccos |x|$

Отражение относительно оси Ox

• Все $y$-значения становятся отрицательными.
• Теперь максимум при $x = 0$ — это минимум: $y = -\frac{\pi}{2}$

Шаг 4: $y = -2 \arccos |x|$

Растяжение по оси $y$ в 2 раза от оси Ox:

• Умножаем все значения $y$ на 2
• Например:
  • $x = 0$: $y = -2 \cdot \frac{\pi}{2} = -\pi$
  • $x = \pm 1$: $y = -2 \cdot 0 = 0$

Итоговый график:

г) $y = \arccos |x — 2|$

Шаг 1: $y = \arccos x$ — стандартный график.

Шаг 2: $x \to x — 2$

Сдвиг графика на 2 единицы вправо по оси $x$

• Область определения сдвигается: теперь $x \in [1, 3]$
• График идёт от точки $x = 1 \Rightarrow y = \arccos(-1) = \pi$, до $x = 3 \Rightarrow y = \arccos(1) = 0$

Шаг 3: Преобразование $|x — 2|$

Что происходит:

• Мы берём правую часть графика (где $x — 2 \ge 0 \Rightarrow x \ge 2$)
• Отражаем её относительно вертикальной прямой $x = 2$

Итоговый график: