ГДЗ по Алгебре 10 Класс Номер 21.40 Профильный Уровень Мордкович — Подробные Ответы

Постройте график функции:

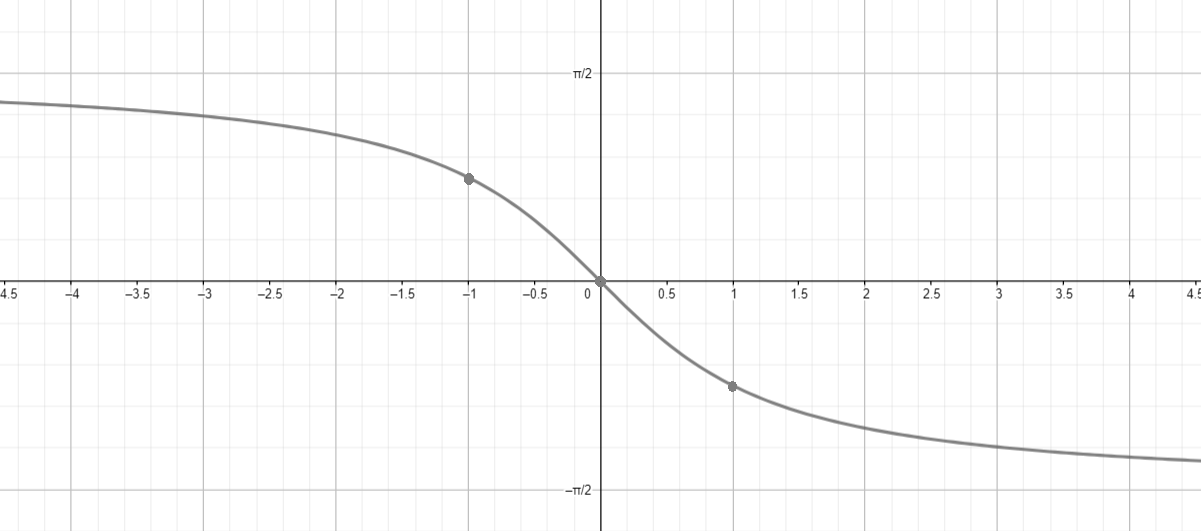
а) у = arctg(-x);

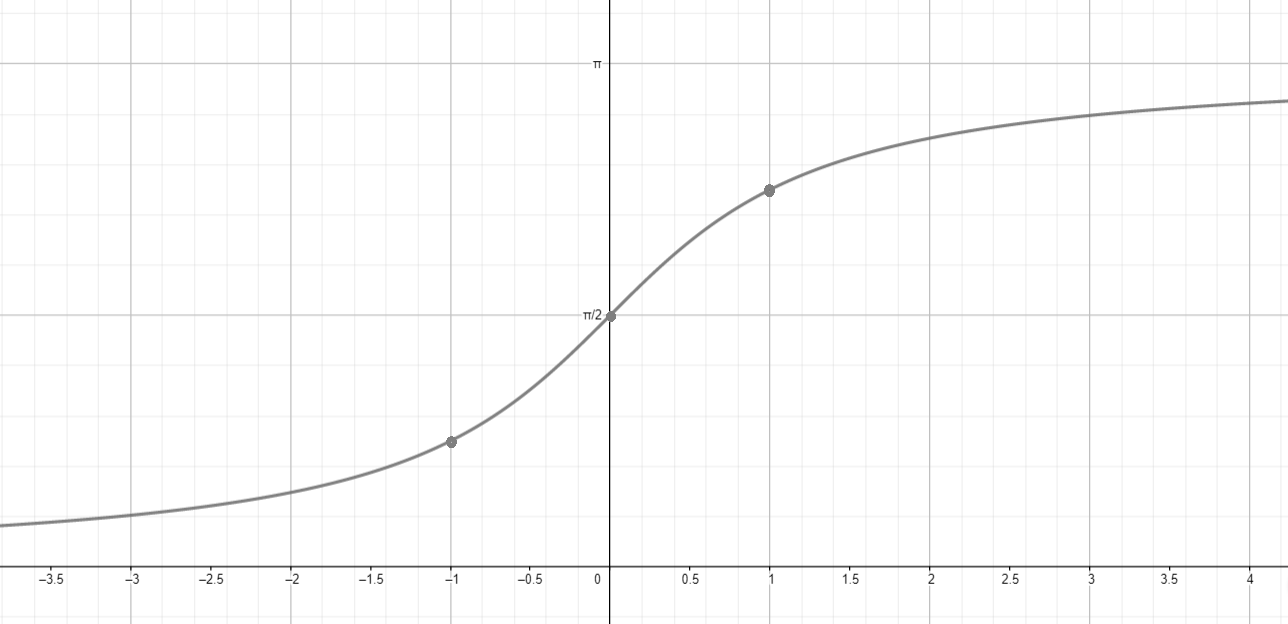
б) у = arcctg(-x);

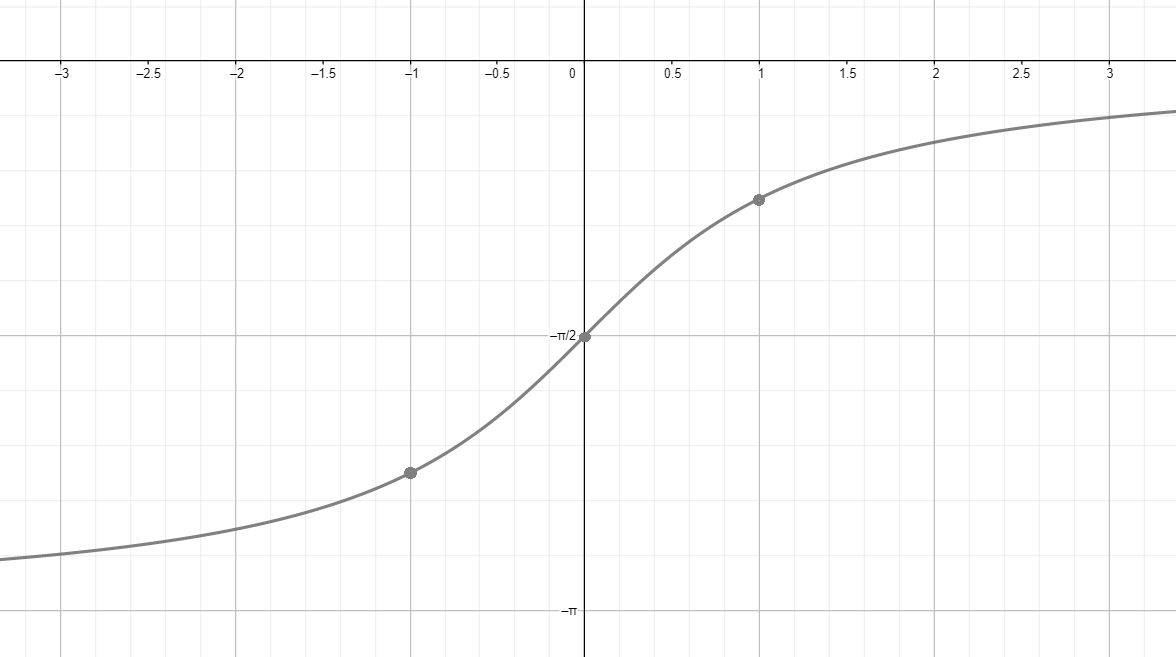
в) у = -arcctgx;

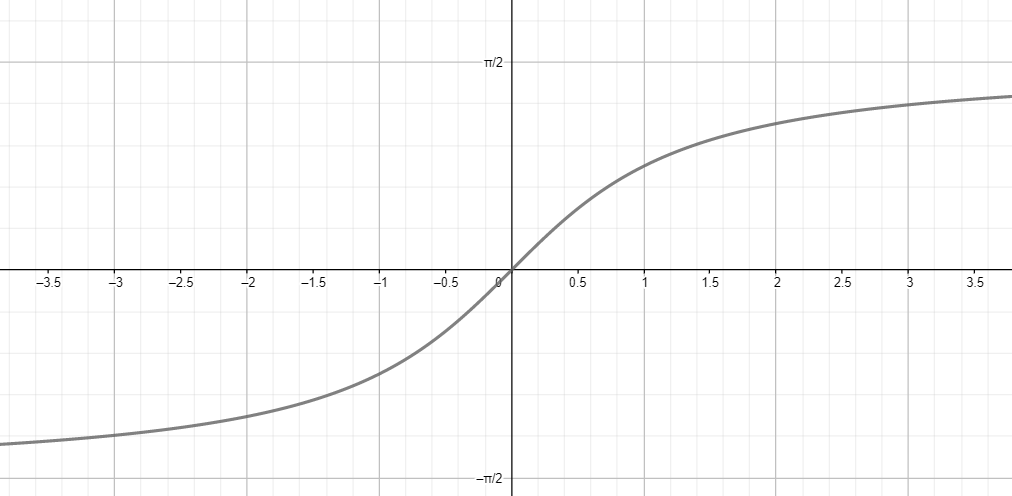
г) у = -arctg(-x).

а) $y = \operatorname{arctg}(-x)$;

Построим график функции $y = \operatorname{arctg} x$;

Отразим его относительно оси ординат:

б) $y = \operatorname{arcctg}(-x)$;

Построим график функции $y = \operatorname{arcctg} x$;

Отразим его относительно оси ординат:

в) $y = -\operatorname{arcctg} x$;

Построим график функции $y = \operatorname{arcctg} x$;

Отразим его относительно оси абсцисс:

г) $y = -\operatorname{arctg}(-x) = \operatorname{arctg} x$;

Построим график функции $y = \operatorname{tg} x$ на отрезке $\left[ -\frac{\pi}{2}; \frac{\pi}{2} \right]$;

Отразим его относительно прямой $y = x$:

а) $y = \operatorname{arctg}(-x)$

Построим график функции $y = \operatorname{arctg} x$:

• Функция $y = \operatorname{arctg} x$ — это обратная функция к тангенсу. Она определена для всех $x \in \mathbb{R}$ и принимает значения в интервале $\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)$.
• График функции $y = \operatorname{arctg} x$ — это гладкая кривая, которая асимптотически приближается к прямым $y = \frac{\pi}{2}$ и $y = -\frac{\pi}{2}$ при $x \to \infty$ и $x \to -\infty$ соответственно.

Отразим график относительно оси ординат:

• Отражение функции относительно оси ординат означает замену $x$ на $-x$ в функции. Для функции $y = \operatorname{arctg}(-x)$ мы получаем, что:

  $$y = \operatorname{arctg}(-x)$$

• График $y = \operatorname{arctg}(-x)$ является зеркальным отражением графика $y = \operatorname{arctg} x$ относительно оси $y$. Это означает, что при положительном $x$ функция принимает отрицательные значения, а при отрицательном $x$ — положительные.
• Симметрия графика относительно оси $y$ сохраняет форму кривой, но отражает её на противоположную сторону.

б) $y = \operatorname{arcctg}(-x)$

Построим график функции $y = \operatorname{arcctg} x$:

• Функция $y = \operatorname{arcctg} x$ — это обратная функция к котангенсу. Она определена для всех $x \in \mathbb{R}$ и принимает значения в интервале $(0, \pi)$.
• График функции $y = \operatorname{arcctg} x$ представляет собой гладкую кривую, которая асимптотически приближается к прямым $y = 0$ при $x \to \infty$ и $y = \pi$ при $x \to -\infty$.

Отразим график относительно оси ординат:

• Отражение функции относительно оси ординат означает замену $x$ на $-x$ в функции. Для функции $y = \operatorname{arcctg}(-x)$ мы получаем:

  $$y = \operatorname{arcctg}(-x)$$

• График $y = \operatorname{arcctg}(-x)$ является зеркальным отражением графика $y = \operatorname{arcctg} x$ относительно оси $y$. Таким образом, форма графика остаётся неизменной, но значения функции при положительных $x$ и отрицательных $x$ меняются местами.
• Это отражение меняет направление графика, но сохраняет его форму. При этом $\operatorname{arcctg}(-x)$ принимает значения от $\pi$ к $0$ при $x \to \infty$, и от $0$ к $\pi$ при $x \to -\infty$.

в) $y = -\operatorname{arcctg} x$

Построим график функции $y = \operatorname{arcctg} x$:

• Как и в предыдущих случаях, график функции $y = \operatorname{arcctg} x$ имеет вид кривой, которая асимптотически приближается к прямым $y = 0$ при $x \to \infty$ и $y = \pi$ при $x \to -\infty$.

Отразим график относительно оси абсцисс:

• Отражение функции относительно оси абсцисс означает изменение знака $y$ на противоположный, то есть замену $y$ на $-y$. Для функции $y = -\operatorname{arcctg} x$ получаем:

  $$y = -\operatorname{arcctg} x$$

• Это отражение переворачивает график функции, меняя его направление. Если график функции $y = \operatorname{arcctg} x$ растёт от $\pi$ до $0$, то график функции $y = -\operatorname{arcctg} x$ будет убывать от $0$ до $-\pi$.
• График сохраняет свою форму, но все значения функции инвертируются.

г) $y = -\operatorname{arctg}(-x) = \operatorname{arctg} x$

Построим график функции $y = \operatorname{tg} x$ на отрезке $\left[ -\frac{\pi}{2}; \frac{\pi}{2} \right]$:

• Функция $y = \operatorname{tg} x$ — это тангенс, который имеет вертикальные асимптоты в точках $x = \pm \frac{\pi}{2}$.
• На отрезке $\left[ -\frac{\pi}{2}; \frac{\pi}{2} \right]$ график функции будет представлять собой кривую, которая проходит через начало координат, стремится к бесконечности при $x \to \frac{\pi}{2}$ и к минус бесконечности при $x \to -\frac{\pi}{2}$.

Отразим график относительно прямой $y = x$:

• Отражение графика функции относительно прямой $y = x$ означает, что все точки графика с координатами $(x, y)$ будут перевёрнуты и перенесены в точку с координатами $(y, x)$.
• Таким образом, отражение графика функции $y = \operatorname{tg} x$ относительно прямой $y = x$ даёт график функции $y = \operatorname{arctg} x$. Это связано с тем, что график $y = \operatorname{tg} x$ и график $y = \operatorname{arctg} x$ являются взаимно обратными функциями, и их графики взаимно симметричны относительно прямой $y = x$.

Итоговые шаги для каждого пункта:

а) Построить график функции $y = \operatorname{arctg} x$, затем отразить его относительно оси ординат.

б) Построить график функции $y = \operatorname{arcctg} x$, затем отразить его относительно оси ординат.

в) Построить график функции $y = \operatorname{arcctg} x$, затем отразить его относительно оси абсцисс.

г) Построить график функции $y = \operatorname{tg} x$ на отрезке $\left[ -\frac{\pi}{2}; \frac{\pi}{2} \right]$, затем отразить его относительно прямой $y = x$.