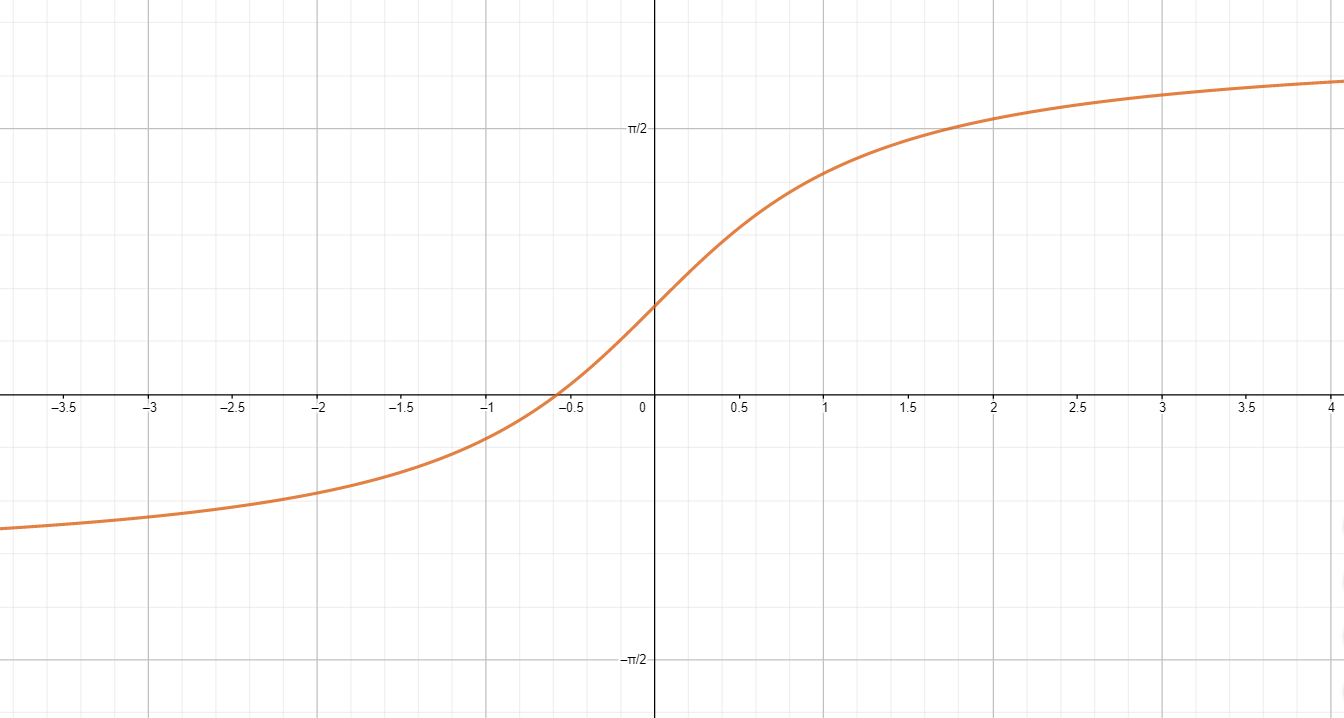ГДЗ по Алгебре 10 Класс Номер 21.42 Профильный Уровень Мордкович — Подробные Ответы

Постройте график функции:

а) $y = 0,5 \arctg x$;

б) $y = \frac{2\pi}{3} — \arctg x$;

в) $y = -\frac{1}{3} \arctg x$;

г) $y=1,5\mathrm{arctg}(x+2)$

а) $y = 0,5 \arctg x$;

Построим график функции $y = \arctg x$;

Сожмем его к оси $Ox$ с коэффициентом $k = 2$:

б) $y = \frac{2\pi}{3} — \arctg x$;

Построим график функции $y = \arctg x$;

Отразим его относительно оси абсцисс;

Переместим его на $\frac{2\pi}{3}$ единиц вверх вдоль оси ординат:

в) $y = -\frac{1}{3} \arctg x$;

Построим график функции $y = \arctg x$;

Отразим его относительно оси абсцисс;

Сожмем его к оси $Ox$ с коэффициентом $k = 3$:

г) $y = 1,5 \arctg(x + 2)$;

Построим график функции $y = \arctg x$;

Переместим его на 2 единицы влево вдоль оси абсцисс;

Растянем его от оси $Ox$ с коэффициентом $k = 1,5$:

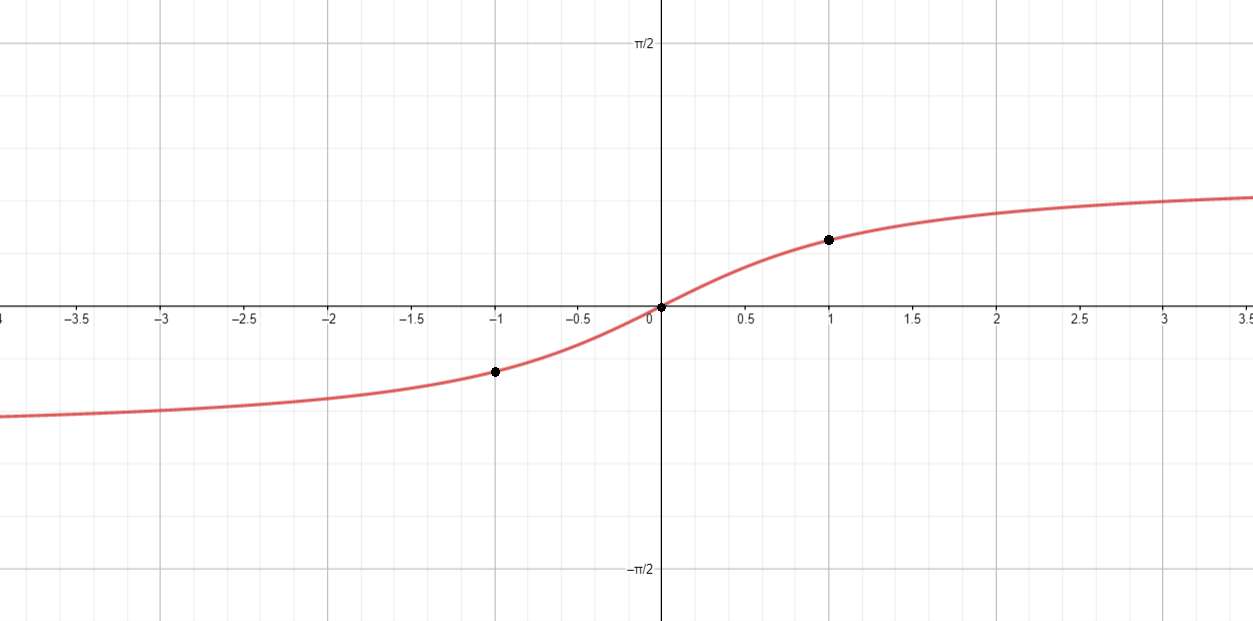
а) $y = 0,5 \arctg x$

Построим график функции $y = \arctg x$:

• Функция $y = \arctg x$ (обратный арктангенс) определена для всех $x \in \mathbb{R}$.
• График функции имеет вертикальные асимптоты при $x \to \pm \infty$, стремясь к значениям $y = \frac{\pi}{2}$ для $x \to +\infty$ и $y = -\frac{\pi}{2}$ для $x \to -\infty$.
• График функции представляет собой гладкую S-образную кривую, которая проходит через точку $(0, 0)$.

Сожмем график функции к оси $Ox$ с коэффициентом $k = 2$:

• Сжатие графика функции вдоль оси $Ox$ с коэффициентом $k = 2$ означает, что для каждого $x$ значение функции $y = \arctg x$ будет уменьшаться в два раза. Для этого нужно умножить функцию на $0,5$, то есть:

  $$y = 0,5 \arctg x$$

• Сжатие графика функции приводит к тому, что форма кривой сохраняется, но она становится «плоской» в два раза, то есть значения функции при каждом $x$ уменьшены в два раза.
• Это сжатие графика графика вдоль оси $y$ (вертикально), и график становится более «плоским».

б) $y = \frac{2\pi}{3} — \arctg x$

Построим график функции $y = \arctg x$:

• График функции $y = \arctg x$ уже был построен в пункте а.

Отразим его относительно оси абсцисс:

• Отражение графика относительно оси абсцисс означает изменение знака $y$ на противоположный, то есть $y = — \arctg x$. Для этого нужно просто заменить знак перед функцией, что приведет к изменению направления графика:

  $$y = -\arctg x$$

• График функции будет зеркально отражен относительно оси $x$. То есть, если раньше график функции $y = \arctg x$ стремился к $\frac{\pi}{2}$ при $x \to +\infty$ и $-\frac{\pi}{2}$ при $x \to -\infty$, то после отражения значения при $x \to +\infty$ будут стремиться к $-\frac{\pi}{2}$, а при $x \to -\infty$ к $\frac{\pi}{2}$.

Переместим его на $\frac{2\pi}{3}$ единиц вверх вдоль оси ординат:

• Перемещение графика вверх на $\frac{2\pi}{3}$ единиц означает добавление $\frac{2\pi}{3}$ к функции:

  $$y = -\arctg x + \frac{2\pi}{3}$$

• Все точки на графике сдвигаются на $\frac{2\pi}{3}$ единиц вверх, то есть точка пересечения с осью $y$ из $(0, 0)$ сдвигается в точку $(0, \frac{2\pi}{3})$.

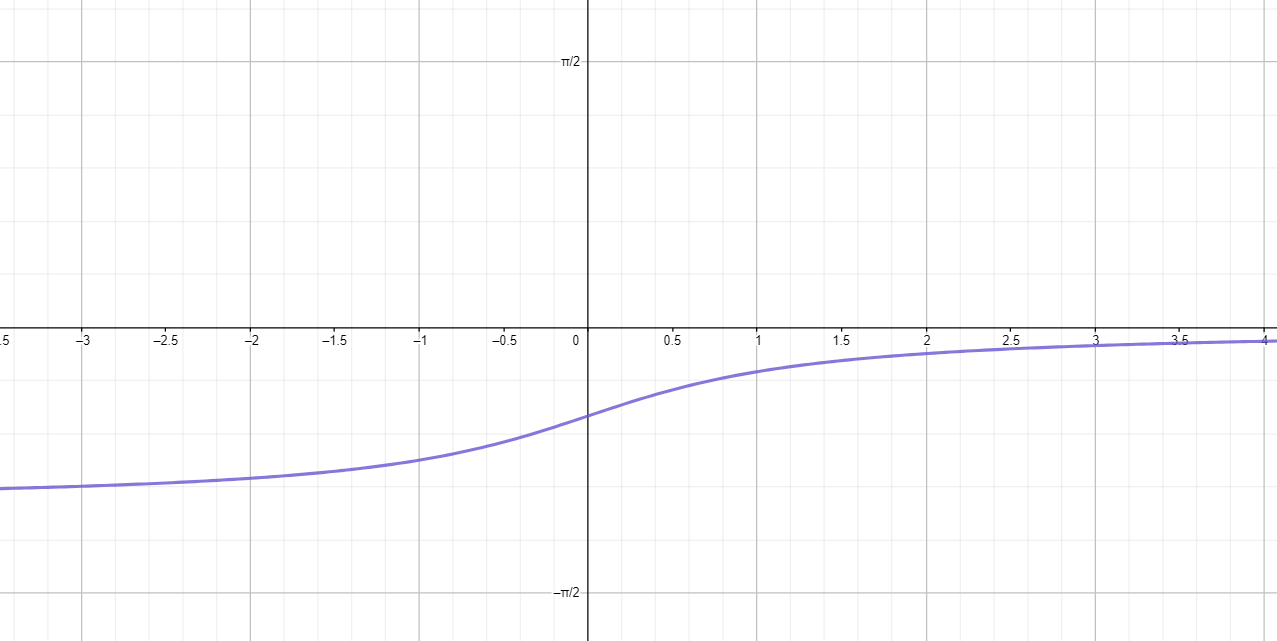
в) $y = -\frac{1}{3} \arctg x$

Построим график функции $y = \arctg x$:

• График функции $y = \arctg x$ уже был построен в пункте а.

Отразим его относительно оси абсцисс:

• Отражение относительно оси абсцисс снова означает изменение знака перед функцией:

  $$y = — \arctg x$$

• График функции будет зеркально отражен относительно оси $x$, как мы рассматривали в пункте б.

Сожмем его к оси $Ox$ с коэффициентом $k = 3$:

• Сжатие графика функции вдоль оси $Ox$ с коэффициентом $k = 3$ означает, что значения функции будут уменьшаться в 3 раза для каждого значения $x$. Это можно выразить, умножив функцию на $\frac{1}{3}$:

  $$y = -\frac{1}{3} \arctg x$$

• Сжатие графика функции приводит к тому, что кривая становится более «плоской» в три раза по сравнению с исходным графиком. То есть значения функции для каждого $x$ уменьшены в 3 раза.
• Таким образом, график остается с теми же асимптотами, но становится «более пологим».

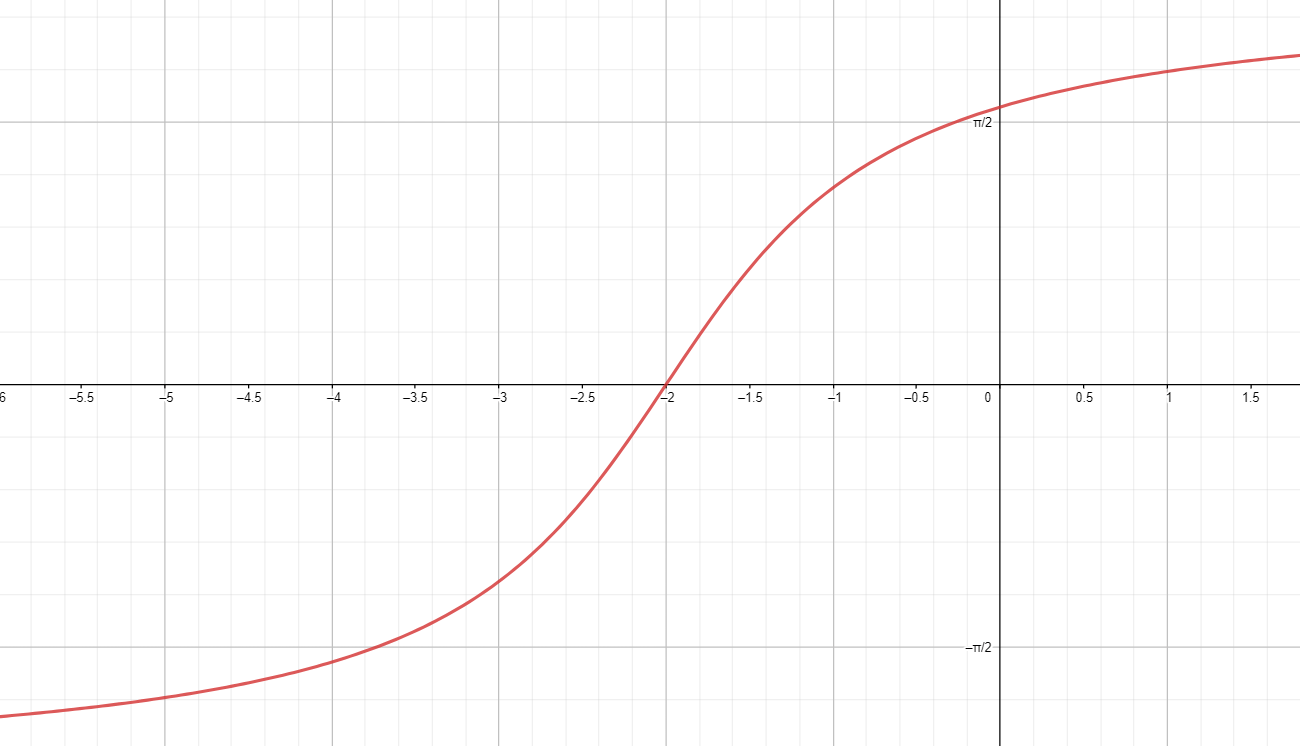
г) $y = 1,5 \arctg(x + 2)$

Построим график функции $y = \arctg x$:

• График функции $y = \arctg x$ уже был построен в пункте а.

Переместим его на 2 единицы влево вдоль оси абсцисс:

• Это означает замену $x$ на $x + 2$ в функции, то есть:

  $$y = \arctg(x + 2)$$

• Перемещение графика на 2 единицы влево сдвигает график на 2 единицы влево вдоль оси $x$, и точка пересечения с осью $x$ из $(0, 0)$ сдвигается в точку $(-2, 0)$.

Растянем его от оси $Ox$ с коэффициентом $k = 1,5$:

• Растяжение графика функции вдоль оси $Ox$ с коэффициентом $k = 1,5$ означает, что для каждого значения $x$ результат функции $y$ будет увеличен в 1,5 раза. Это можно выразить, умножив функцию на $1,5$:

  $$y = 1,5 \arctg(x + 2)$$

• Растяжение графика приводит к тому, что форма графика становится «более крутой» и «выше» по сравнению с исходным графиком. То есть значения функции при каждом $x$ увеличиваются в 1,5 раза.