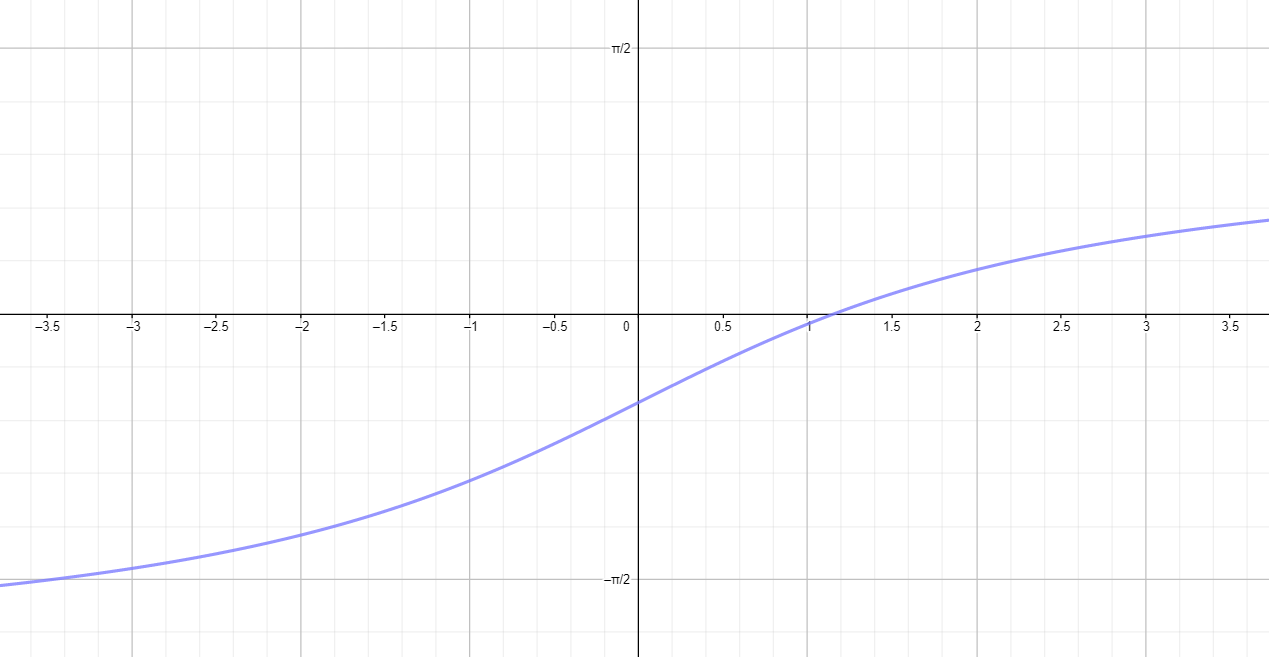ГДЗ по Алгебре 10 Класс Номер 21.43 Профильный Уровень Мордкович — Подробные Ответы

Постройте график функции:

а) $y = \operatorname{arctg} 3x$;

б) $y = \operatorname{arctg} \frac{x}{2} — \frac{\pi}{6}$;

в) $y = \operatorname{arcctg} \frac{3x}{4}$;

г) $y=\mathrm{arcctg}2(x-1)$

а) $y = \operatorname{arctg} 3x$;

Построим график функции $y = \operatorname{arctg} x$;

Сожмем его к оси $Oy$ с коэффициентом $k = 3$:

б) $y = \operatorname{arctg} \frac{x}{2} — \frac{\pi}{6}$;

Построим график функции $y = \arcsin x$;

Растянем его от оси $Oy$ с коэффициентом $k = 2$;

Переместим его на $\frac{\pi}{6}$ единиц вниз вдоль оси ординат:

в) $y = \operatorname{arcctg} \frac{3x}{4}$;

Построим график функции $y = \operatorname{arcctg} x$;

Растянем его от оси $Oy$ с коэффициентом $k = 1,3$:

г) $y = \operatorname{arcctg} 2(x — 1)$;

Построим график функции $y = \operatorname{arcctg} x$;

Сожмем его к оси $Oy$ с коэффициентом $k = 2$;

Переместим его на 1 единицу вправо вдоль оси абсцисс:

а) $y = \operatorname{arctg} 3x$

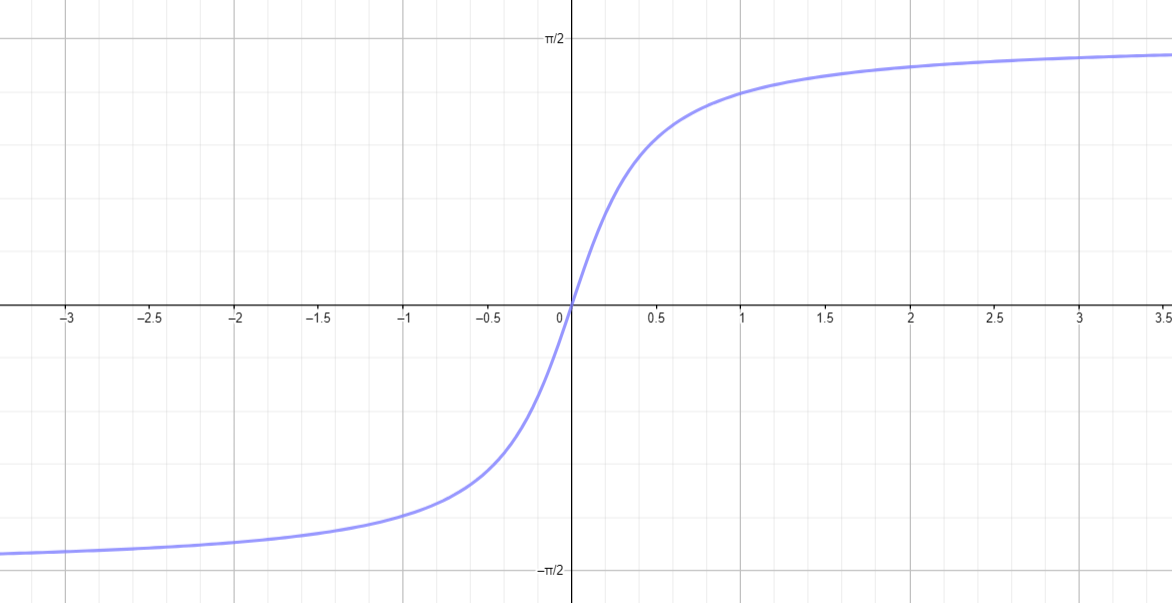
Построим график функции $y = \operatorname{arctg} x$:

• Функция $y = \operatorname{arctg} x$ (обратный арктангенс) имеет вид S-образной кривой. График функции асимптотически приближается к прямым $y = \frac{\pi}{2}$ для $x \to +\infty$ и $y = -\frac{\pi}{2}$ для $x \to -\infty$.
• График проходит через точку $(0, 0)$, и функция растет от $-\frac{\pi}{2}$ до $\frac{\pi}{2}$, когда $x$ меняется от $-\infty$ до $+\infty$.

Сожмем его к оси $Oy$ с коэффициентом $k = 3$:

• Чтобы сжать график функции к оси $Oy$ с коэффициентом $k = 3$, нужно домножить аргумент функции $x$ на 3, что приведет к изменению выражения на:

  $$y = \operatorname{arctg}(3x)$$

• Это сжатие вдоль оси $x$ происходит, потому что теперь график функции изменяется быстрее: при том же значении $x$ значение функции $y$ будет больше (в 3 раза быстрее изменяться).
• Это означает, что функция будет «сжата» вдоль оси $x$, график станет «более крутым» и быстрее достигнет асимптот $\frac{\pi}{2}$ и $-\frac{\pi}{2}$ при меньших значениях $x$.

б) $y = \operatorname{arctg} \frac{x}{2} — \frac{\pi}{6}$

Построим график функции $y = \arcsin x$:

• Вероятно, это ошибка, так как в задачах обычно требуют работать с одной функцией. Мы будем рассматривать $y = \operatorname{arctg} x$, так как именно она используется в самой задаче.
• График функции $y = \operatorname{arctg} x$ уже был построен в предыдущем пункте, и форма этого графика сохраняется.

Растянем его от оси $Oy$ с коэффициентом $k = 2$:

• Для растяжения графика функции от оси $Oy$ с коэффициентом $k = 2$, нужно изменить аргумент $x$ на $\frac{x}{2}$, что будет выглядеть так:

  $$y = \operatorname{arctg}\left(\frac{x}{2}\right)$$

• Это растяжение вдоль оси $x$ приводит к тому, что значения функции начинают изменяться медленнее. График будет «более пологим» и растягиваться вдоль оси $x$.

Переместим его на $\frac{\pi}{6}$ единиц вниз вдоль оси ординат:

• Чтобы переместить график на $\frac{\pi}{6}$ единиц вниз, нужно вычесть $\frac{\pi}{6}$ из выражения для функции:

  $$y = \operatorname{arctg}\left(\frac{x}{2}\right) — \frac{\pi}{6}$$

• Это означает, что весь график сдвигается вниз на $\frac{\pi}{6}$ единиц, что приводит к тому, что точка пересечения с осью $y$ смещается в точку $(0, -\frac{\pi}{6})$.

в) $y = \operatorname{arcctg} \frac{3x}{4}$

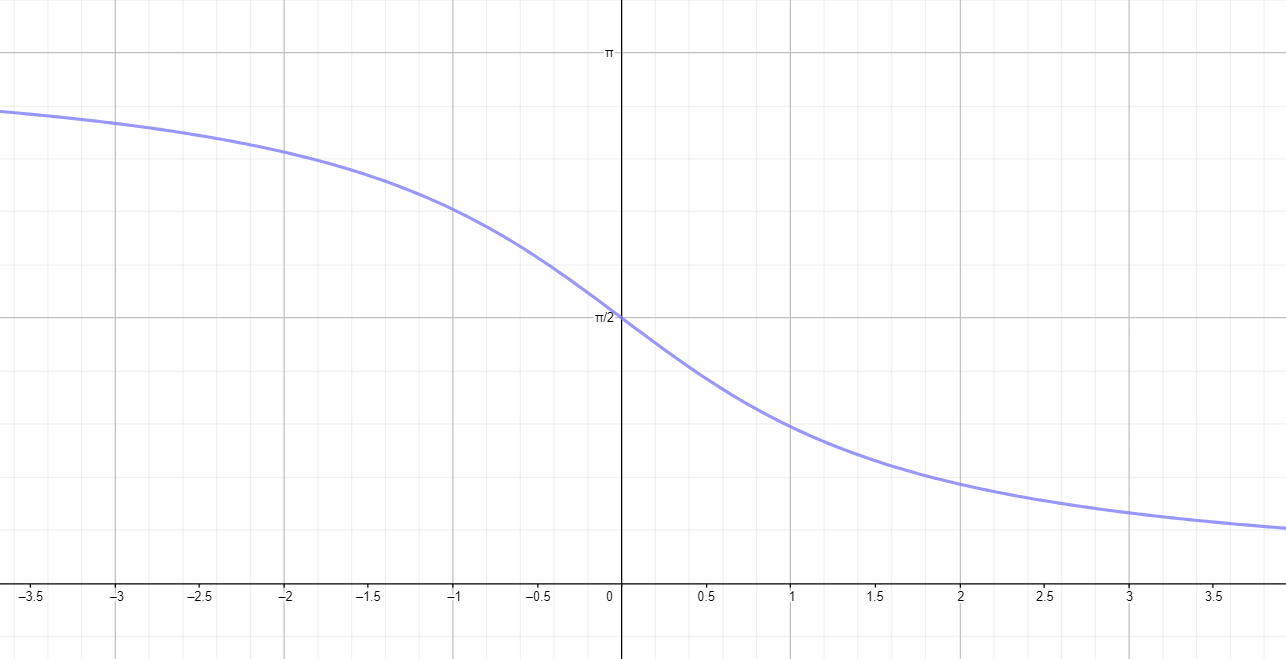
Построим график функции $y = \operatorname{arcctg} x$:

• Функция $y = \operatorname{arcctg} x$ (обратный котангенс) имеет график, который асимптотически приближается к прямым $y = 0$ для $x \to +\infty$ и $y = \pi$ для $x \to -\infty$.
• График функции проходит через точку $(0, \frac{\pi}{2})$.

Растянем его от оси $Oy$ с коэффициентом $k = 1,3$:

• Для растяжения графика функции от оси $Oy$ с коэффициентом $k = 1,3$, нужно умножить аргумент функции $x$ на $\frac{3}{4}$:

  $$y = \operatorname{arcctg}\left(\frac{3x}{4}\right)$$

• Это растяжение приводит к тому, что функция изменяется медленнее. График будет более «пологим», чем исходный.

г) $y = \operatorname{arcctg} 2(x — 1)$

Построим график функции $y = \operatorname{arcctg} x$:

• График функции $y = \operatorname{arcctg} x$ уже был рассмотрен.

Сожмем его к оси $Oy$ с коэффициентом $k = 2$:

• Сжатие графика к оси $Oy$ с коэффициентом $k = 2$ означает, что функция изменяется быстрее. Для этого заменим $x$ на $2(x — 1)$, что будет выглядеть так:

  $$y = \operatorname{arcctg}\left(2(x — 1)\right)$$

• Это сжатие приводит к тому, что функция теперь будет изменяться в два раза быстрее, и график станет более крутым.

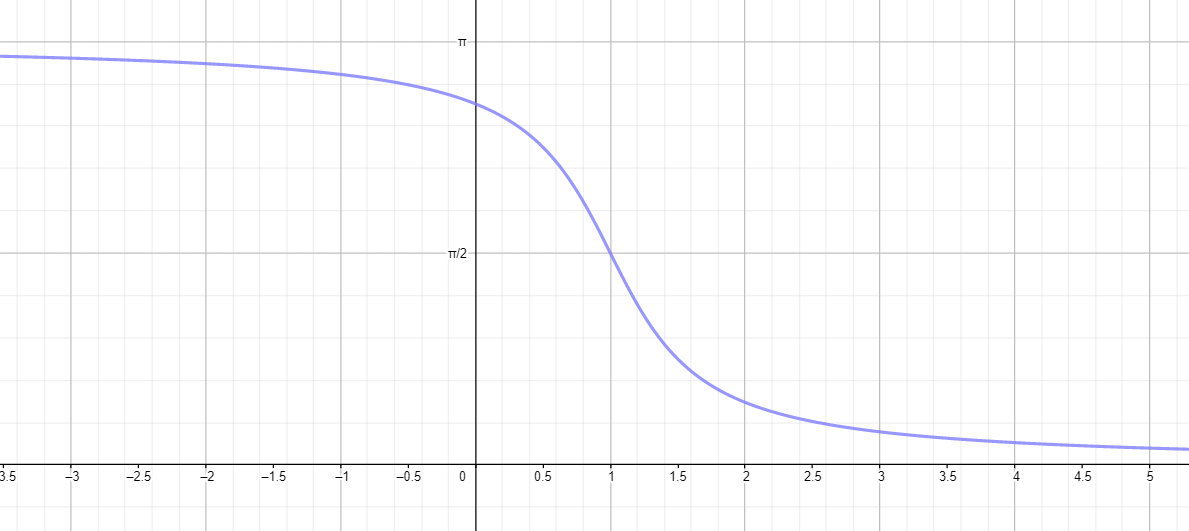
Переместим его на 1 единицу вправо вдоль оси абсцисс:

• Для сдвига графика на 1 единицу вправо вдоль оси $x$, нужно заменить $x$ на $x — 1$ в аргументе:

  $$y = \operatorname{arcctg}(2(x — 1))$$

• Это сдвигает график на 1 единицу вправо вдоль оси $x$, то есть точка, где график пересекает ось $y$, будет сдвигаться на 1 единицу вправо.