ГДЗ по Алгебре 10 Класс Номер 21.44 Профильный Уровень Мордкович — Подробные Ответы

Постройте и прочитайте график функции:

а) $y=\{\begin{array}{ll}\mathrm{arctg}x,& \text{если }x\le 0\\ \sqrt{x},& \text{если }x>0\end{array}$

б) $y=\{\begin{array}{ll}\mathrm{arctg}x,& \text{если }x\le 1\\ \mathrm{arctg}x,& \text{если }x>1\end{array}$

а) $y = \begin{cases} \arctg x, & \text{если } x \leq 0 \\ \sqrt{x}, & \text{если } x > 0 \end{cases};$

$y = \arctg x$ — обратная функция:
$y(0) = \arctg 0 = 0;$

$y = \sqrt{x}$ — уравнение ветви параболы:
$x_0 = 0, \, y_0 = 0;$

Графики функций:

Свойства функции:

• Область определения: $D(f) = (-\infty; +\infty);$
• Множество значений: $E(f) = \left( -\frac{\pi}{2}; +\infty \right);$
• Возрастает на $(-\infty; +\infty);$
• $f(x) > 0$ на $(0; +\infty);$
• $f(x) \leq 0$ на $(-\infty; 0);$
• Функция ни четная, ни нечетная;
• Функция не является периодической;

б) $y = \begin{cases} \arctg x, & \text{если } x \leq 1 \\ \arctg x, & \text{если } x > 1 \end{cases};$

$y = \arctg x$ — обратная функция:
$y(1) = \arctg 1 = \frac{\pi}{4};$

$y = \arctg x$ — обратная функция:
$y(1) = \arctg 1 = \frac{\pi}{4};$

Графики функций:

Свойства функции:

• Область определения: $D(f) = (-\infty; +\infty);$
• Множество значений: $E(f) = \left[ \frac{\pi}{4}; +\infty \right);$
• Возрастает на $[1; +\infty);$
• Убывает на $(-\infty; 1];$
• $f(x) > 0$ на $(-\infty; +\infty);$
• Функция ни четная, ни нечетная;
• Функция не является периодической

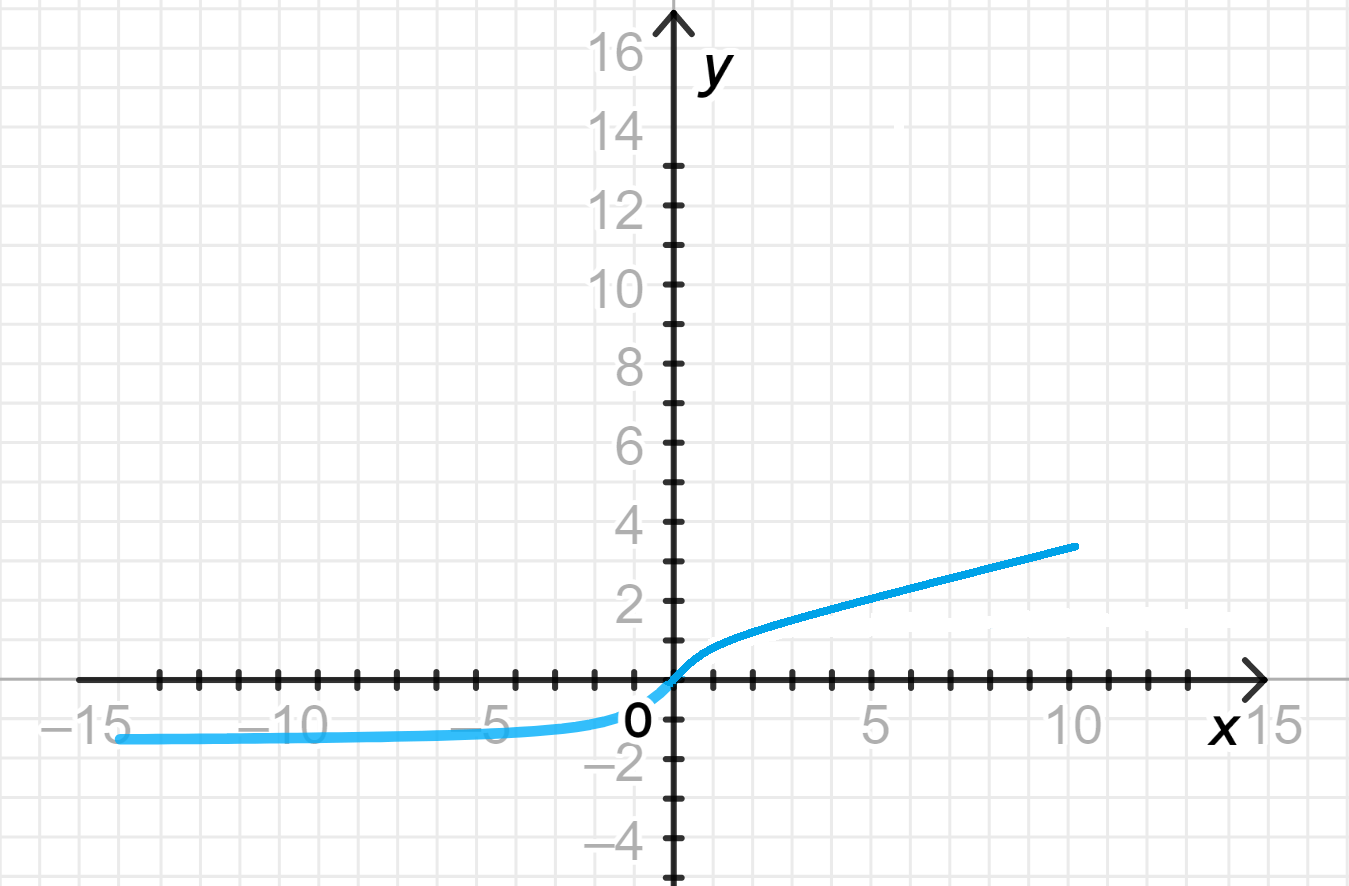
а)

Функция:

$$y = \begin{cases} \arctg x, & \text{если } x \leq 0 \\ \sqrt{x}, & \text{если } x > 0 \end{cases}$$

1. Рассмотрим первую ветвь функции $y = \arctg x$ при $x \leq 0$:

• $y = \arctg x$ — обратная тригонометрическая функция, которая для всех значений $x$ принимает значения из интервала $\left( -\frac{\pi}{2}; \frac{\pi}{2} \right)$.
• Для $x = 0$ $y = \arctg 0 = 0$.

2. Рассмотрим вторую ветвь функции $y = \sqrt{x}$ при $x > 0$:

• Эта часть функции является стандартной квадратной коренью, которая определена только для положительных значений $x$.
• Для $x = 0$ $y = \sqrt{0} = 0$.

Теперь найдем несколько значений этой функции для разных $x$:

• $x = 0, \quad y = 0$
• $x = 1, \quad y = \sqrt{1} = 1$
• $x = 4, \quad y = \sqrt{4} = 2$

Составим таблицу:

3. Построение графика

4. Свойства функции:

• Область определения: $D(f) = (-\infty; +\infty)$, так как обе части функции определены на всей числовой оси.
• Множество значений: $E(f) = \left( -\frac{\pi}{2}; +\infty \right)$. Это обусловлено тем, что функция $y = \arctg x$ принимает значения в интервале $\left( -\frac{\pi}{2}; \frac{\pi}{2} \right)$, а функция $y = \sqrt{x}$ принимает значения от 0 до $+\infty$.
• Возрастание: Функция возрастает на всей области определения $(-\infty; +\infty)$, так как обе составляющие функции монотонно возрастают.
• Значения на разных интервалах:
  • $f(x) > 0$ для $x > 0$, так как $\sqrt{x} \geq 0$.
  • $f(x) \leq 0$ для $x \leq 0$, так как $\arctg x$ принимает отрицательные значения при $x < 0$ и 0 при $x = 0$.
• Четность: Функция не является ни четной, ни нечетной.
  • Для четности, должно выполняться условие $f(-x) = f(x)$, но это не выполняется для данной функции.
• Периодичность: Функция не является периодической, так как обе ее части не повторяются на фиксированных интервалах.

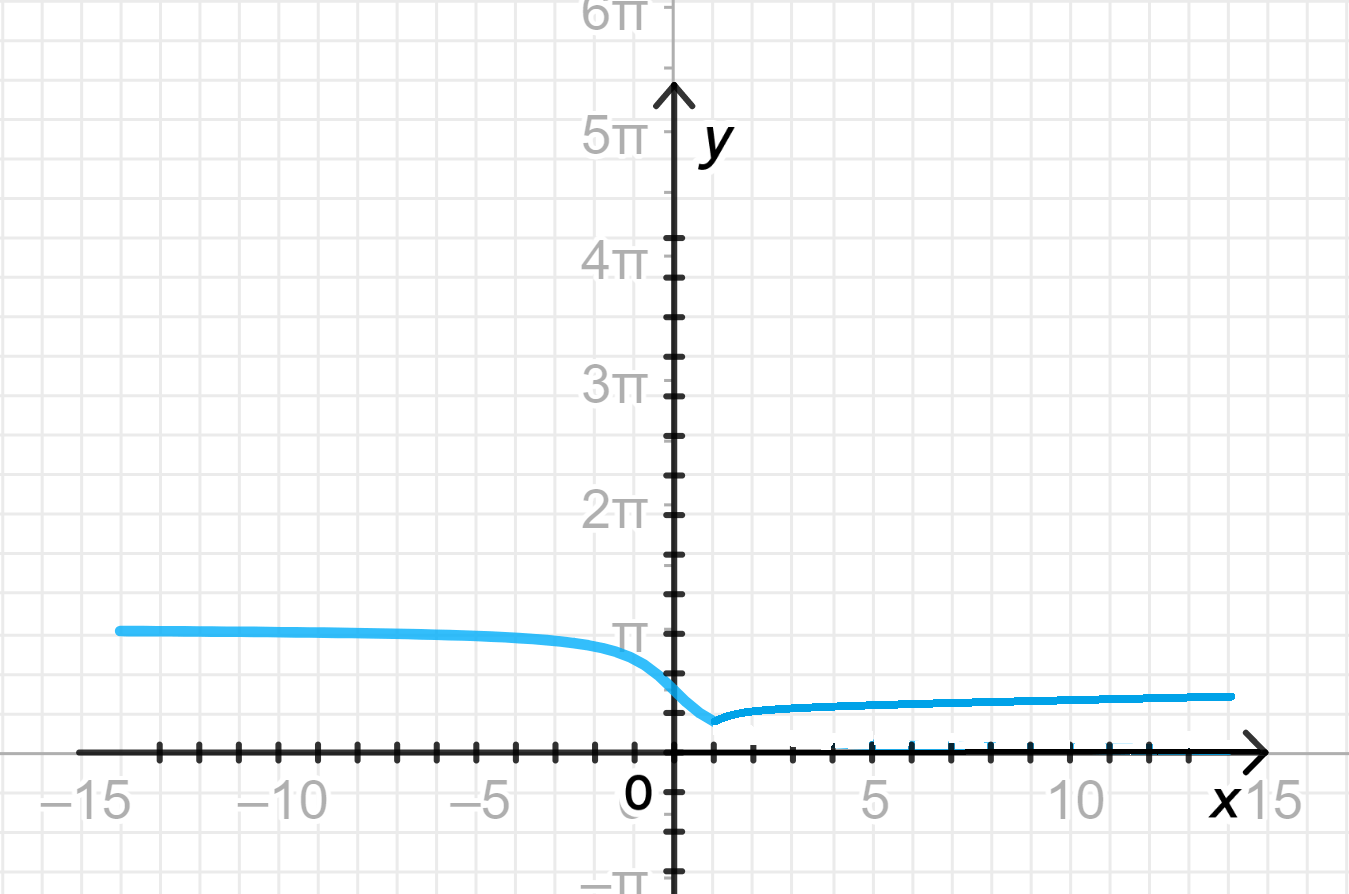
б)

Функция:

$$y = \begin{cases} \arctg x, & \text{если } x \leq 1 \\ \arctg x, & \text{если } x > 1 \end{cases}$$

1. Рассмотрим функцию $y = \arctg x$ для $x \leq 1$:

• Эта ветвь функции принимает значения от $-\frac{\pi}{2}$ до $\arctg(1) = \frac{\pi}{4}$.
• Для $x = 1$ $y = \arctg 1 = \frac{\pi}{4}$.

2. Рассмотрим функцию $y = \arctg x$ для $x > 1$:

• Эта ветвь функции для значений $x > 1$ будет продолжением предыдущей ветви, она возрастает и стремится к $\frac{\pi}{2}$ при $x \to \infty$.
• Для $x = 1$ $y = \arctg 1 = \frac{\pi}{4}$, что совпадает с предыдущим значением.

3. Построение графика

4. Свойства функции:

• Область определения: $D(f) = (-\infty; +\infty)$, так как функция $\arctg x$ определена на всей числовой оси.
• Множество значений: $E(f) = \left[ \frac{\pi}{4}; +\frac{\pi}{2} \right)$, так как функция $y = \arctg x$ принимает значения от $\frac{\pi}{4}$ при $x = 1$ до $\frac{\pi}{2}$ при $x \to \infty$.
• Возрастание:
  • Функция возрастает на интервале $(-\infty; 1]$ и на интервале $[1; +\infty)$.
  • На интервале $(-\infty; 1]$ она убывает.
• Четность: Функция не является четной, так как для четности должно выполняться условие $f(-x) = f(x)$, что не выполняется.
• Периодичность: Функция не является периодической.