ГДЗ по Алгебре 10 Класс Номер 21.45 Профильный Уровень Мордкович — Подробные Ответы

Постройте график функции:

а) $y = |\arctg x|$;

б) $y = \arcctg |x|$;

в) $y = -2 \arcctg |x|$;

г) $y=\mid \mathrm{arctg}x+\frac{\pi }{6}\mid$

а) $y = |\arctg x|$;

Построим график функции $y = \arctg x$;

Отразим относительно оси $Ox$ часть графика, лежащую под ней.

б) $y = \arcctg |x|$;

Построим график функции $y = \arcctg x$;

Уберем часть графика, лежащую слева от оси $Oy$;

Отразим относительно нее часть графика, лежащую справа.

в) $y = -2 \arcctg |x|$;

Построим график функции $y = \arcctg x$;

Отразим его относительно оси абсцисс;

Уберем часть графика, лежащую слева от оси $Oy$;

Отразим относительно нее часть графика, лежащую справа;

Растянем график от оси $Ox$ с коэффициентом $k = 2$.

г) $y = \left| \arctg x + \frac{\pi}{6} \right|$;

Построим график функции $y = \arctg x$;

Переместим его на $\frac{\pi}{6}$ единиц вверх вдоль оси ординат;

Отразим относительно оси $Ox$ часть графика, лежащую под ней.

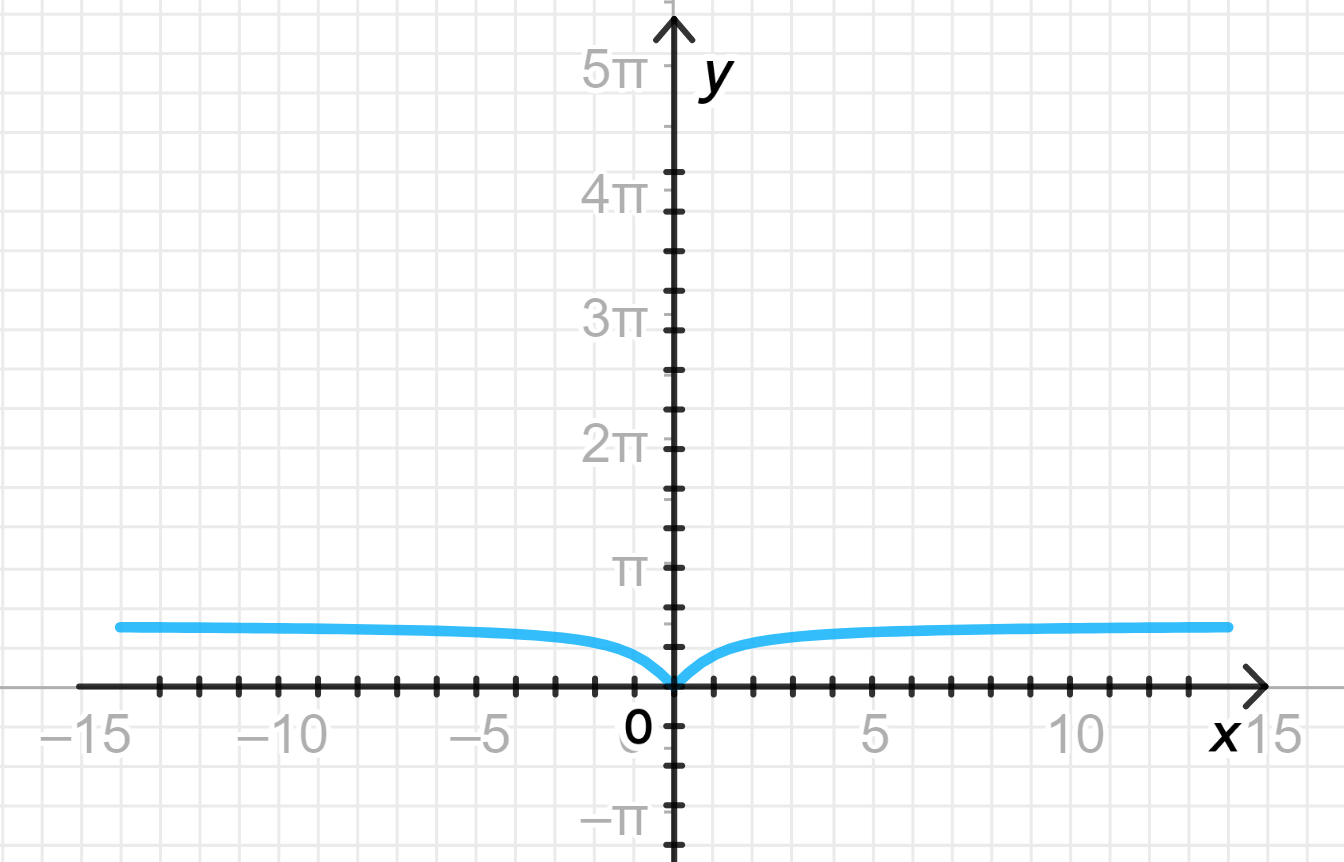
а)

Функция:

$$y = |\arctg x|$$

Шаг 1: Построим график функции $y = \arctg x$

• Функция $\arctg x$ является обратной функцией для тангенса и определена для всех $x \in (-\infty; +\infty)$.
• График $y = \arctg x$ представляет собой гладкую кривую, которая проходит через точку $(0, 0)$, а также имеет горизонтальные асимптоты:
  • При $x \to -\infty$, $y \to -\frac{\pi}{2}$,
  • При $x \to +\infty$, $y \to \frac{\pi}{2}$.

График выглядит следующим образом:

• На интервале $(-\infty; +\infty)$ функция монотонно возрастает от $-\frac{\pi}{2}$ до $\frac{\pi}{2}$.

Шаг 2: Отразим относительно оси $Ox$ часть графика, лежащую под ней

• Для функции $y = |\arctg x|$, необходимо отразить все отрицательные значения функции $\arctg x$ относительно оси $Ox$.
• Это приведет к тому, что для всех $x$, где $\arctg x$ было отрицательным, значение функции станет положительным.
• Таким образом, функция $y = |\arctg x|$ будет:
  • Для $x \geq 0$, график совпадает с графиком $y = \arctg x$,
  • Для $x < 0$, график будет симметричен относительно оси $Ox$, и принимает положительные значения.

Результат:

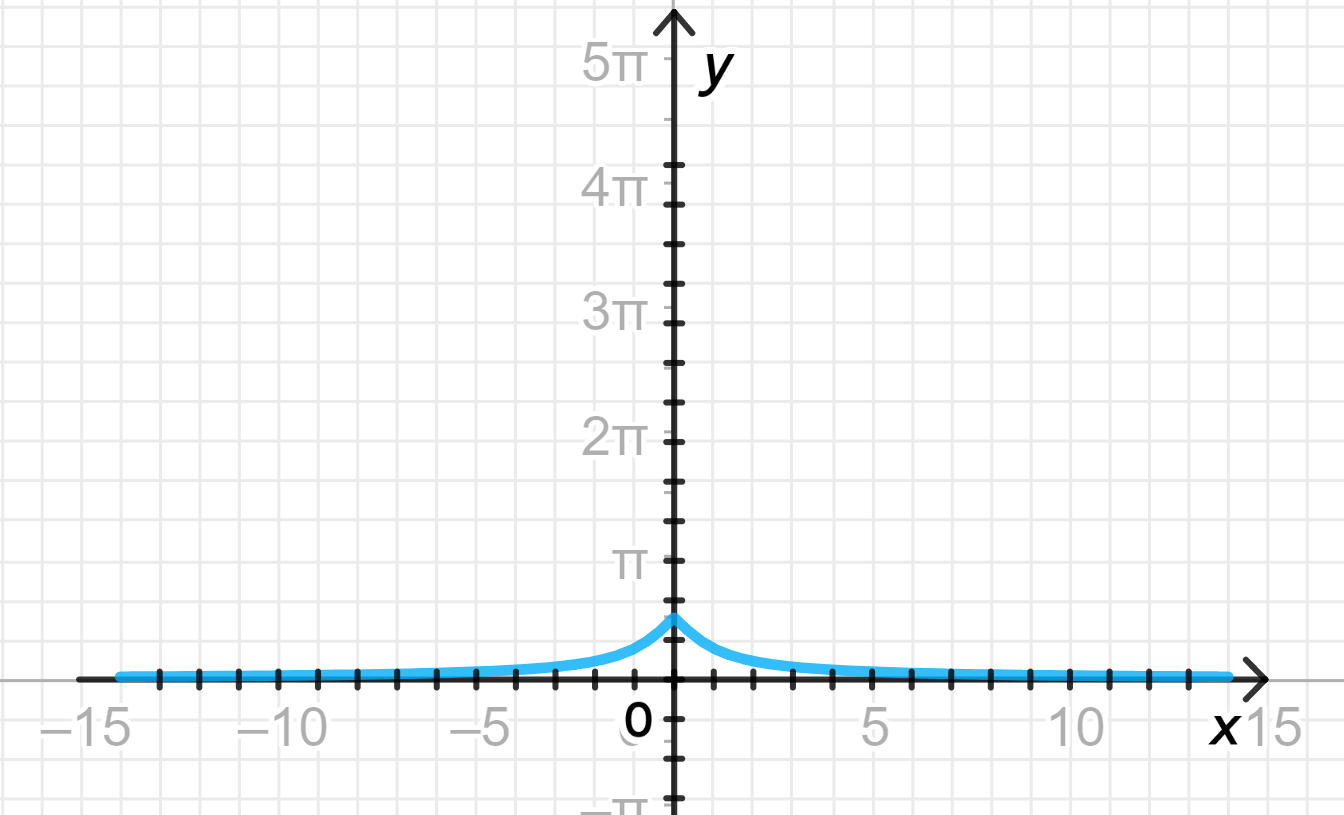
б)

Функция:

$$y = \arcctg |x|$$

Шаг 1: Построим график функции $y = \arcctg x$

• Функция $\arcctg x$ является обратной функцией для котангенса и определена для всех $x \in (-\infty; +\infty)$.
• График $y = \arcctg x$ представляет собой гладкую кривую, которая проходит через точку $(0, \frac{\pi}{2})$, и имеет горизонтальные асимптоты:
  • При $x \to -\infty$, $y \to 0$,
  • При $x \to +\infty$, $y \to 0$.

Шаг 2: Уберем часть графика, лежащую слева от оси $Oy$

• Мы работаем с абсолютным значением $|x|$, поэтому для $x < 0$ функция $\arcctg |x|$ будет одинаковой, как и для $x > 0$.
• Таким образом, необходимо убрать часть графика, которая расположена слева от оси $Oy$, потому что для отрицательных значений $x$, функция $\arcctg |x|$ будет одинаковой для положительных значений $x$.

Шаг 3: Отразим относительно оси $Oy$ часть графика, лежащую справа

• График для $x > 0$ аналогичен графику $y = \arcctg x$, а для $x < 0$ график будет зеркальным отражением правой части функции относительно оси $Oy$.

Результат:

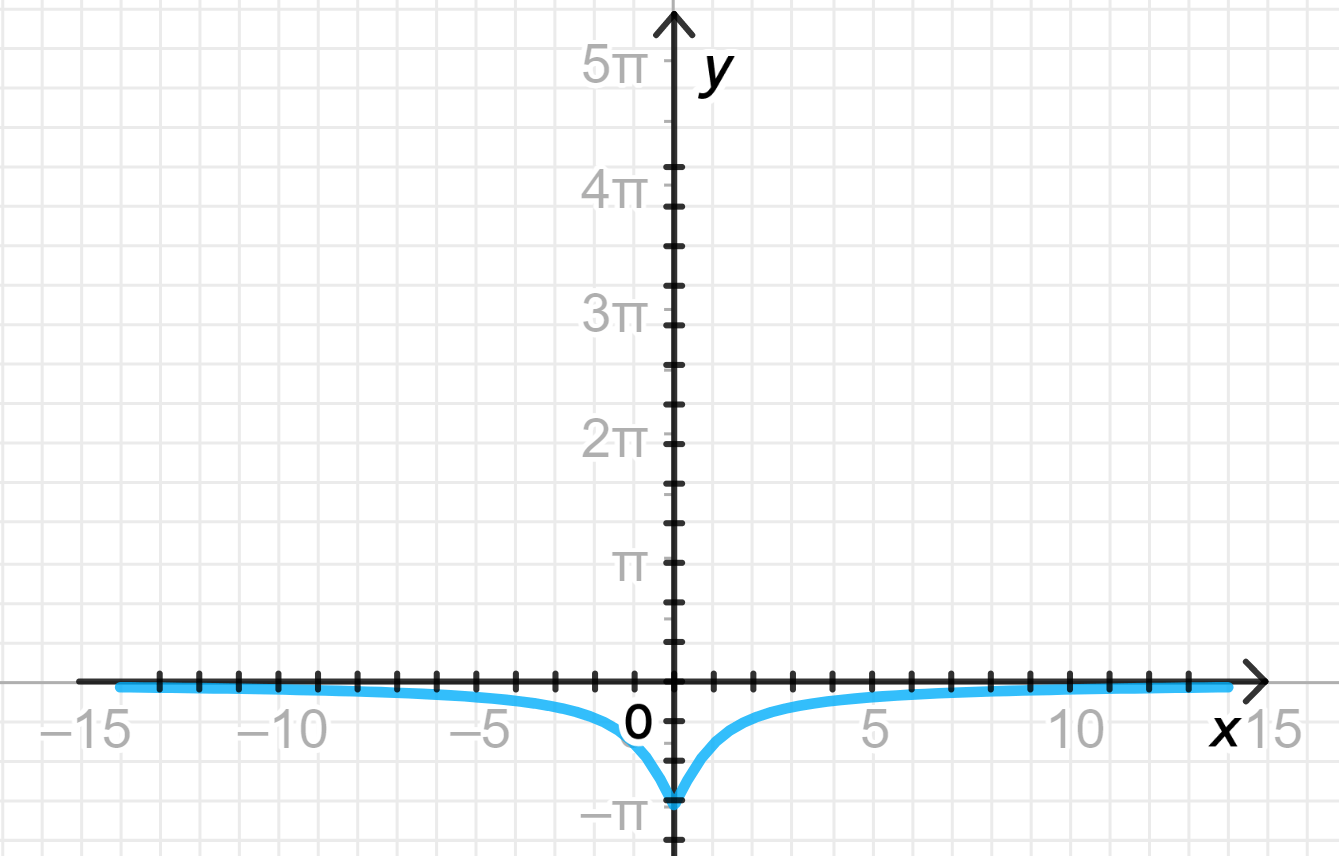
в)

Функция:

$$y = -2 \arcctg |x|$$

Шаг 1: Построим график функции $y = \arcctg x$

• Мы уже рассматривали график функции $y = \arcctg x$. Он возрастает от $\pi$ при $x = 0$ до 0 при $x \to \infty$, а также от $\pi$ до 0 при $x \to -\infty$.

Шаг 2: Отразим его относительно оси абсцисс

• Умножив на $-1$, мы отразим график функции относительно оси абсцисс. Это изменит направление возрастания: теперь график будет убывать, начиная с $-\pi$ при $x = 0$ и стремиться к 0 при $x \to \pm \infty$.

Шаг 3: Уберем часть графика, лежащую слева от оси $Oy$

• График функции для отрицательных значений $x$ будет идентичен графику для положительных значений $x$, так как функция зависит только от $|x|$. Поэтому мы удаляем часть графика, расположенную слева от оси $Oy$.

Шаг 4: Отразим относительно оси $Oy$ часть графика, лежащую справа

• Теперь, для $x > 0$, график будет продолжать оставаться тем же, а для $x < 0$ — зеркально отраженным относительно оси $Oy$.

Шаг 5: Растянем график от оси $Ox$ с коэффициентом $k = 2$

• Умножив на коэффициент 2, мы растягиваем график вдоль оси $Ox$, что означает удлинение графика по горизонтали. Это растяжение приводит к тому, что значения функции $y = -2 \arcctg |x|$ становятся более «растянутыми» по оси абсцисс.

Результат:

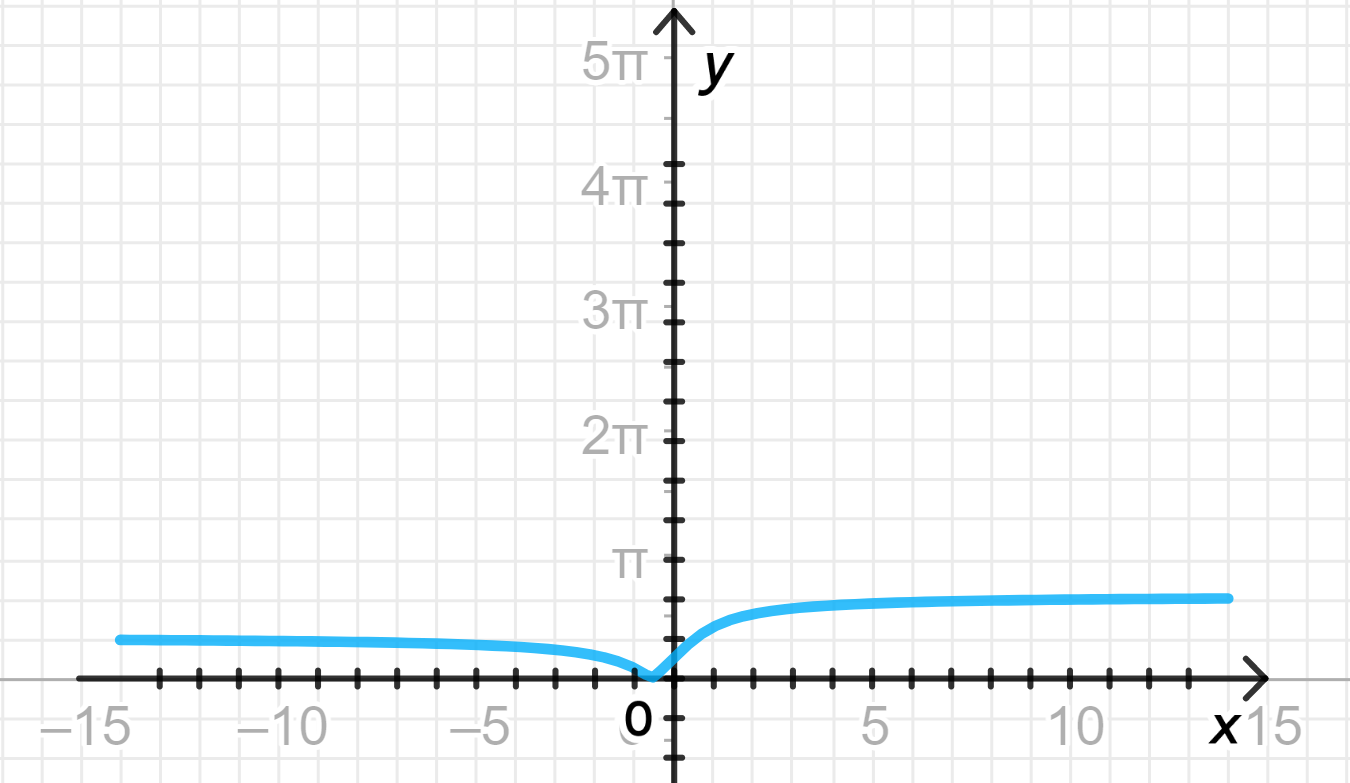
г)

Функция:

$$y = \left| \arctg x + \frac{\pi}{6} \right|$$

Шаг 1: Построим график функции $y = \arctg x$

• Мы уже строили график $y = \arctg x$. Это кривая, которая проходит через точку $(0, 0)$ и имеет горизонтальные асимптоты при $x \to \pm\infty$.

Шаг 2: Переместим его на $\frac{\pi}{6}$ единиц вверх вдоль оси ординат

• Чтобы выполнить сдвиг функции вверх на $\frac{\pi}{6}$, добавляем $\frac{\pi}{6}$ ко всем значениям $y = \arctg x$. Это перемещает всю кривую на $\frac{\pi}{6}$ единиц вверх, изменяя асимптоты и значения функции.

Шаг 3: Отразим относительно оси $Ox$ часть графика, лежащую под ней

• Для всех $x$, где функция $\arctg x + \frac{\pi}{6}$ принимает отрицательные значения, отразим часть графика относительно оси $Ox$. Это обеспечит положительность значений функции для всех $x$.

Результат: