ГДЗ по Алгебре 10 Класс Номер 21.50 Профильный Уровень Мордкович — Подробные Ответы

Постройте график функции:

а) у = cos(arccosx);

б) у = arctgx + arctg(-x);

в) у = tg(arctgx);

г) у = arcsinx + arcsin(-x).

а) $y = \cos(\arccos x) = x$;

Область определения:

$$-1 \leq x \leq 1;$$

График функции:

б) $y = \arctg x + \arctg(-x) = \arctg x — \arctg x = 0$;

Область определения:

$$x \in \mathbb{R};$$

График функции:

в) $y = \tg(\arctg x) = x$;

Область определения:

$$x \in \mathbb{R};$$

График функции:

г) $y = \arcsin x + \arcsin(-x) = \arcsin x — \arcsin x = 0$;

Область определения:

$$-1 \leq x \leq 1;$$

График функции:

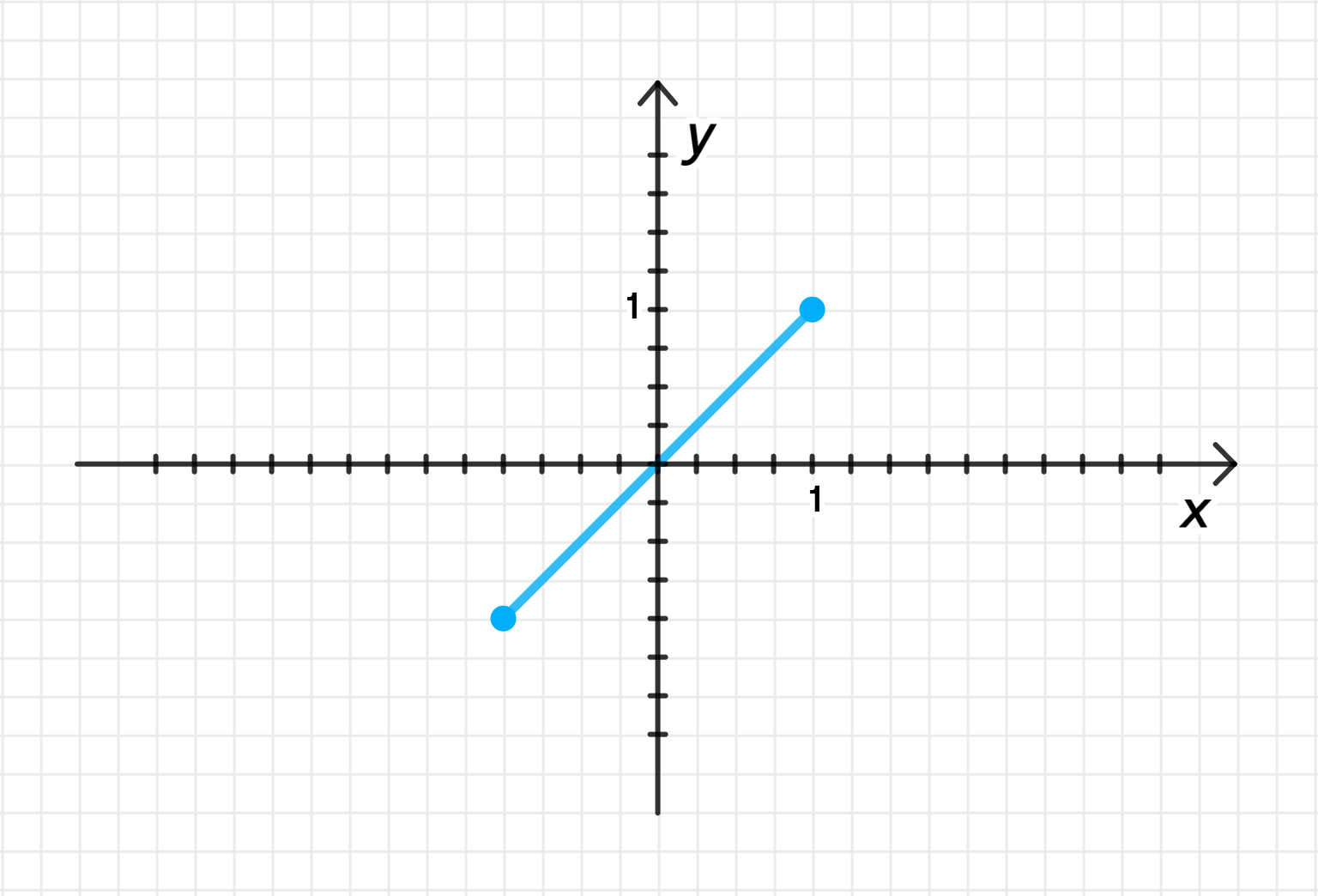
а) $y = \cos(\arccos x) = x$

Область определения:

• Арккосинус $\arccos x$ определен только для значений $x$, которые лежат в интервале $[-1, 1]$. Это связано с тем, что косинус функции $\arccos x$ может принимать значения только в пределах от -1 до 1.
• Следовательно, область определения данной функции:

$$-1 \leq x \leq 1.$$

График функции:

Функция $\cos(\arccos x)$ представляет собой обратную операцию по отношению к $\arccos x$, поскольку $\cos$ и $\arccos$ — это взаимно обратные функции. Таким образом, для любого значения $x$ в пределах области определения $\left[-1, 1\right]$ выполняется равенство:

$$\cos(\arccos x) = x.$$

График функции $y = x$ представляет собой прямую, которая проходит через начало координат с углом наклона 45° относительно оси абсцисс. Эта прямая будет проходить от точки $(-1, -1)$ до $(1, 1)$.

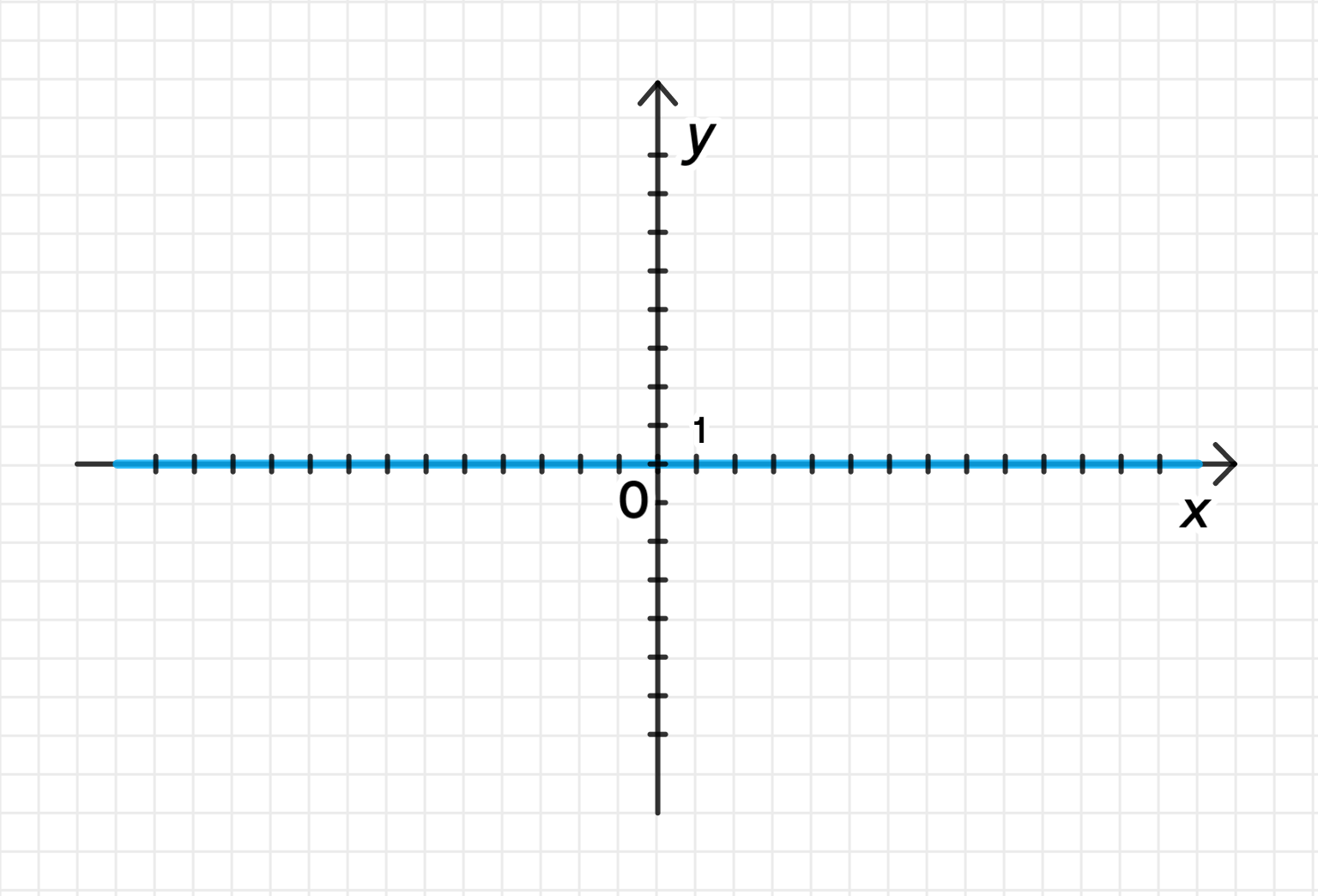
б) $y = \arctg x + \arctg(-x) = \arctg x — \arctg x = 0$

Область определения:

• Арктангенс $\arctg x$ определен для всех $x \in \mathbb{R}$, то есть область определения функции $\arctg x + \arctg(-x)$ — это вся действительная прямая.

$$x \in \mathbb{R}.$$

График функции:

Рассмотрим выражение:

$$\arctg x + \arctg(-x).$$

Поскольку $\arctg(-x)$ является антисимметричной функцией относительно оси $y$, то:

$$\arctg(-x) = -\arctg(x).$$

Следовательно:

$$\arctg x + \arctg(-x) = \arctg x — \arctg x = 0.$$

Таким образом, функция всегда равна 0 для любого $x \in \mathbb{R}$, и график этой функции представляет собой горизонтальную прямую, проходящую через ось $x$ на уровне $y = 0$.

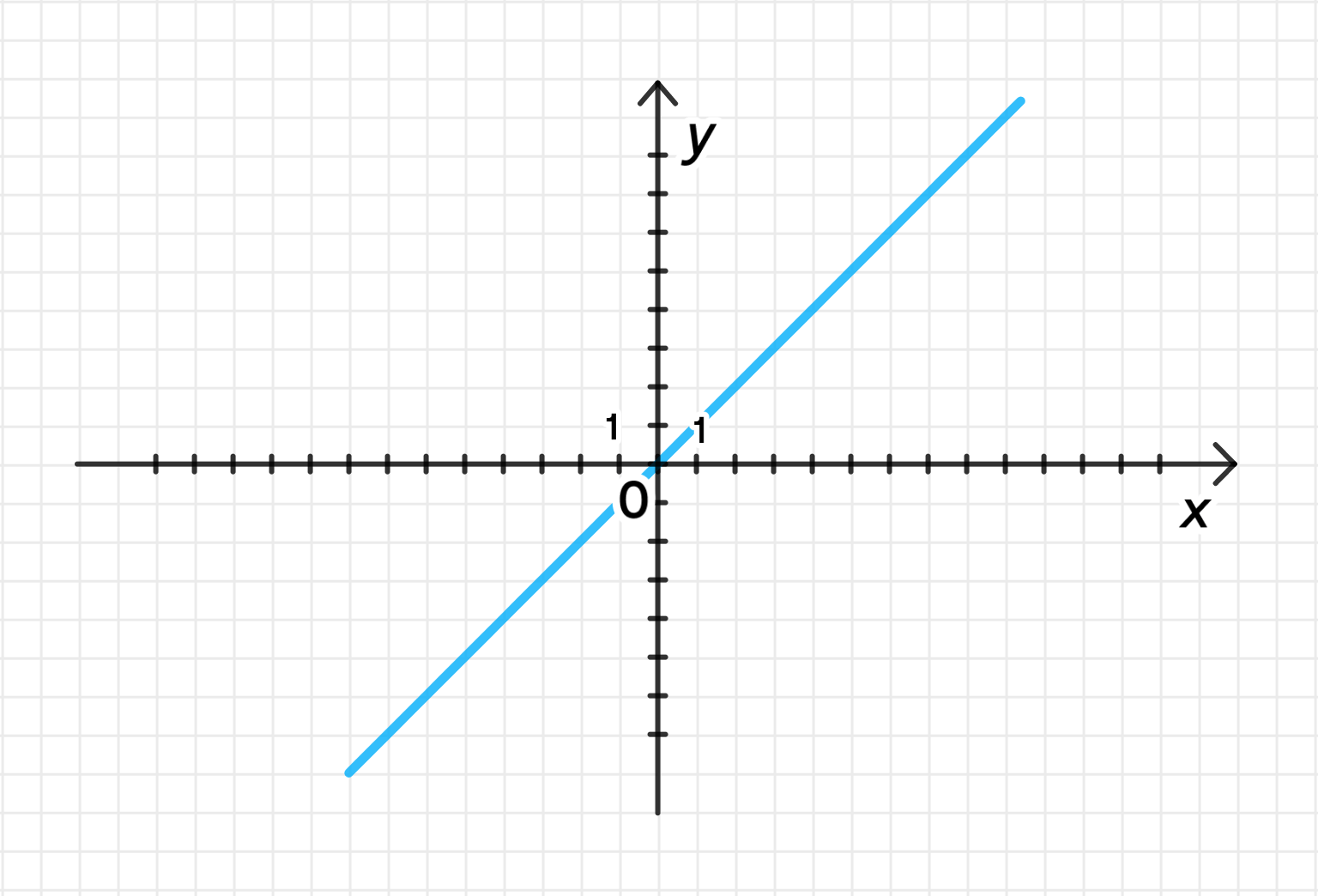
в) $y = \tg(\arctg x) = x$

Область определения:

• Арктангенс $\arctg x$ определен для всех $x \in \mathbb{R}$, а также тангенс $\tg(\arctg x)$ определен для всех действительных чисел.
• Таким образом, область определения данной функции — это вся действительная прямая:

$$x \in \mathbb{R}.$$

График функции:

Поскольку $\arctg x$ — это функция, которая принимает значение угла, чья тангенс равен $x$, то $\tg(\arctg x)$ по сути возвращает значение $x$. Это означает, что:

$$\tg(\arctg x) = x.$$

График функции $y = x$ — это прямая, которая проходит через начало координат с углом наклона 45° относительно оси абсцисс. Эта прямая будет проходить от точки $(-\infty, -\infty)$ до $(\infty, \infty)$.

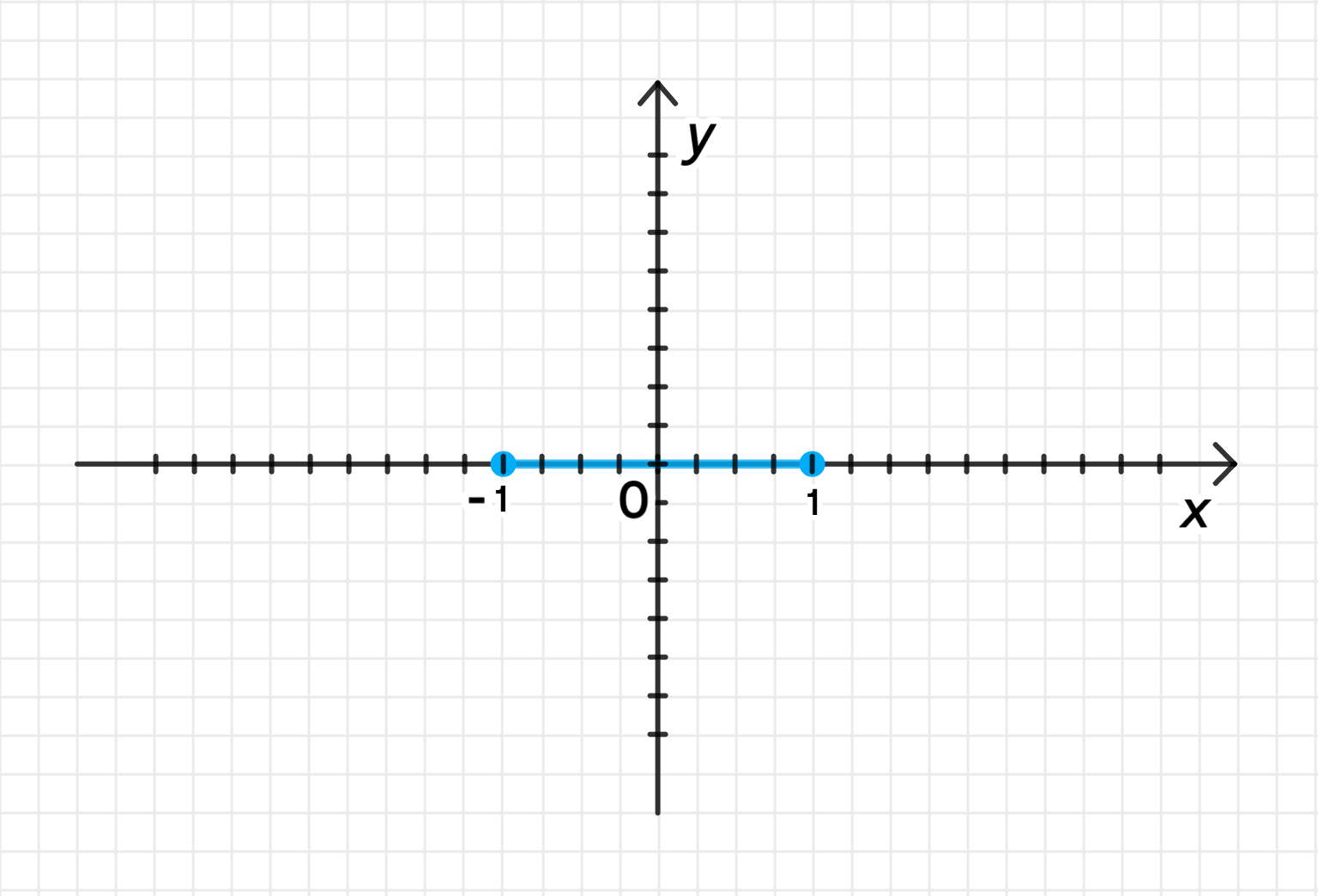
г) $y = \arcsin x + \arcsin(-x) = \arcsin x — \arcsin x = 0$

Область определения:

• Арксинус $\arcsin x$ определен только для значений $x \in [-1, 1]$, так как синус может принимать значения только в этом интервале.
• Следовательно, область определения функции $\arcsin x + \arcsin(-x)$:

$$-1 \leq x \leq 1.$$

График функции:

Рассмотрим выражение:

$$\arcsin x + \arcsin(-x).$$

Поскольку $\arcsin(-x) = -\arcsin(x)$ (арксинус — это нечетная функция), получаем:

$$\arcsin x + \arcsin(-x) = \arcsin x — \arcsin x = 0.$$

Таким образом, функция всегда равна 0 для любого $x \in [-1, 1]$, и график этой функции представляет собой горизонтальную прямую, проходящую через ось $x$ на уровне $y = 0$.

Итоговые результаты:

а) $y = \cos(\arccos x) = x$, область определения: $-1 \leq x \leq 1$, график: прямая $y = x$.

б) $y = \arctg x + \arctg(-x) = 0$, область определения: $x \in \mathbb{R}$, график: горизонтальная прямая $y = 0$.

в) $y = \tg(\arctg x) = x$, область определения: $x \in \mathbb{R}$, график: прямая $y = x$.

г) $y = \arcsin x + \arcsin(-x) = 0$, область определения: $-1 \leq x \leq 1$, график: горизонтальная прямая $y = 0$.