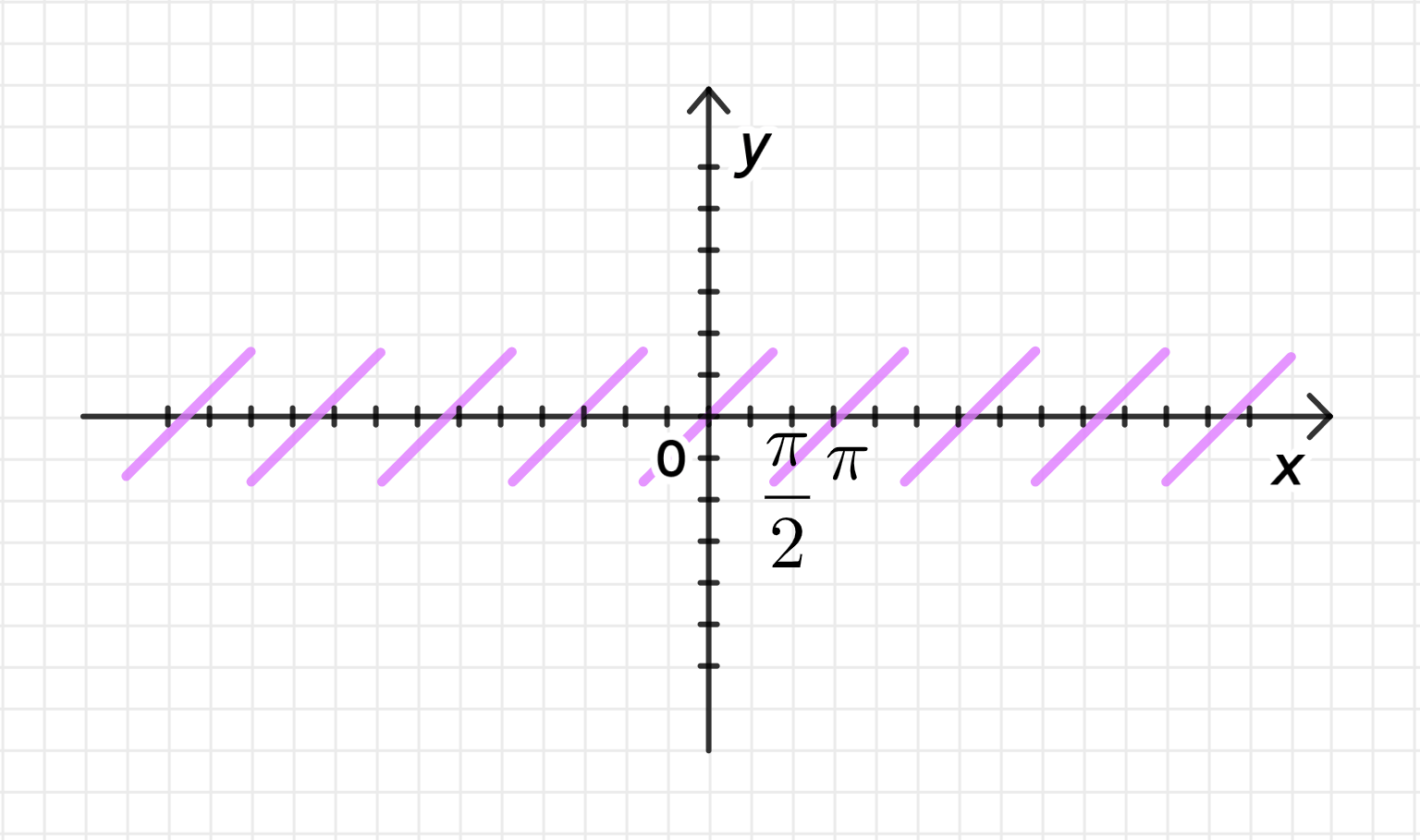ГДЗ по Алгебре 10 Класс Номер 21.53 Профильный Уровень Мордкович — Подробные Ответы

Постройте график функции:

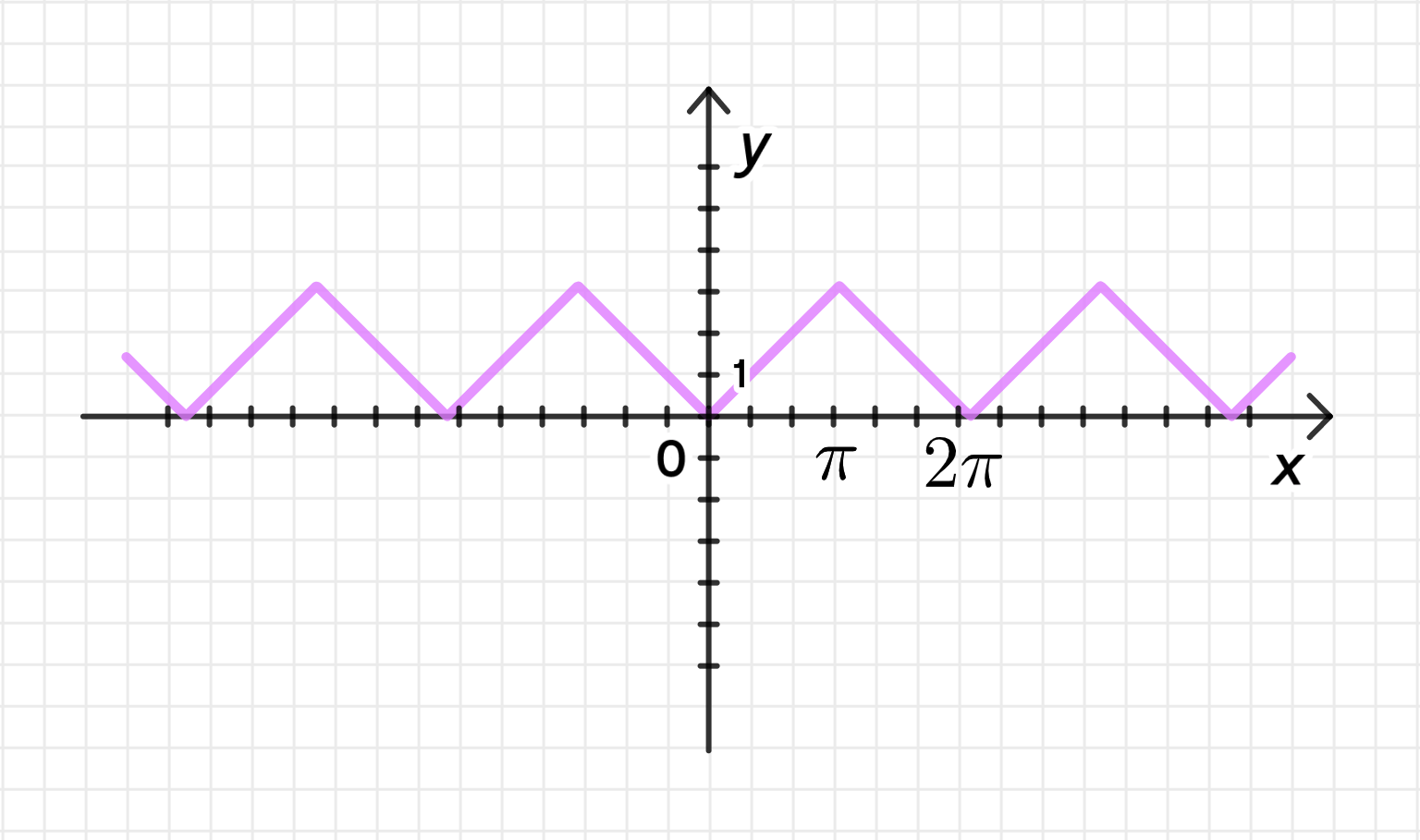
а) у = arccos(cosx);

б) у = arctg(tgx).

а) $y = \arccos(\cos x)$;

Функция является периодической с периодом $T = 2\pi$:

$$y(x + 2\pi) = \arccos(\cos(x + 2\pi)) = \arccos(\cos x) = y(x);$$

Функция является четной:

$$y(-x) = \arccos(\cos(-x)) = \arccos(\cos x) = y(x);$$

На отрезке $[0; \pi]$:

$$\cos x = t;$$ $$y = \arccos(\cos x) = \arccos t = x;$$

График функции:

б) $y = \arctg(\tg x)$;

Функция является периодической с периодом $T = \pi$:

$$y(x + \pi) = \arctg(\tg(x + \pi)) = \arctg(\tg x) = y(x);$$

Функция является нечетной:

$$y(-x) = \arctg(\tg(-x)) = \arctg(-\tg x) = -\arctg(\tg x) = -y(x);$$

На отрезке $\left[0; \frac{\pi}{2}\right]$:

$$\tg x = t;$$ $$y = \arctg(\tg x) = \arctg t = x;$$

Область определения:

$$x \neq \frac{\pi}{2} + \pi n;$$

График функции:

а) $y = \arccos(\cos x)$

Периодичность функции:

Для начала рассмотрим периодичность функции $y = \arccos(\cos x)$. Арккосинус $\arccos x$ является функцией, которая имеет периодичность. Однако важно понимать, что периодичность этой функции зависит от аргумента $\cos x$, который также периодичен с периодом $2\pi$. Таким образом, рассмотрим следующий вывод:

$$y(x + 2\pi) = \arccos(\cos(x + 2\pi)) = \arccos(\cos x) = y(x).$$

Это подтверждает, что функция $\arccos(\cos x)$ является периодической с периодом $T = 2\pi$. Период функции равен $2\pi$, поскольку $\cos(x + 2\pi) = \cos x$, и арккосинус сохраняет это равенство.

Четность функции:

Проверим, является ли функция четной. Для этого вычислим $y(-x)$:

$$y(-x) = \arccos(\cos(-x)) = \arccos(\cos x) = y(x).$$

Таким образом, функция $y = \arccos(\cos x)$ является четной, так как $y(-x) = y(x)$.

Поведение функции на отрезке $[0; \pi]$:

На отрезке $[0; \pi]$ рассмотрим выражение $\cos x = t$. Тогда:

$$y = \arccos(\cos x) = \arccos t = x.$$

Таким образом, на отрезке $[0; \pi]$ функция $\arccos(\cos x)$ представляет собой линейную функцию $y = x$, так как на этом интервале $\arccos(\cos x)$ является монотонной.

График функции:

График функции $y = \arccos(\cos x)$ будет выглядеть как дуга, которая повторяется с периодом $2\pi$. На интервале $[0; \pi]$ функция ведет себя как $y = x$, а затем начинается новое повторение через $2\pi$. То есть график функции будет представлять собой последовательность отрезков, каждый из которых представляет собой прямую линию от $0$ до $\pi$, и затем повторяется.

б) $y = \arctg(\tg x)$

Периодичность функции:

Рассмотрим периодичность функции $y = \arctg(\tg x)$. Тангенс $\tg x$ имеет период $\pi$, то есть $\tg(x + \pi) = \tg x$. Арктангенс $\arctg x$ также периодичен с периодом $\pi$. Следовательно:

$$y(x + \pi) = \arctg(\tg(x + \pi)) = \arctg(\tg x) = y(x).$$

Это подтверждает, что функция $y = \arctg(\tg x)$ является периодической с периодом $T = \pi$.

Нечетность функции:

Теперь проверим, является ли функция нечетной. Для этого вычислим $y(-x)$:

$$y(-x) = \arctg(\tg(-x)) = \arctg(-\tg x) = -\arctg(\tg x) = -y(x).$$

Таким образом, функция $y = \arctg(\tg x)$ является нечетной, так как $y(-x) = -y(x)$.

Поведение функции на отрезке $\left[0; \frac{\pi}{2}\right]$:

На отрезке $\left[0; \frac{\pi}{2}\right]$ рассмотрим выражение $\tg x = t$. Тогда:

$$y = \arctg(\tg x) = \arctg t = x.$$

На этом интервале функция $y = \arctg(\tg x)$ будет линейной функцией $y = x$.

Область определения:

Тангенс не определен в точках, где его аргумент равен $\frac{\pi}{2} + n\pi$, где $n$ — целое число. Таким образом, область определения функции:

$$x \neq \frac{\pi}{2} + \pi n, \quad n \in \mathbb{Z}.$$

График функции:

График функции $y = \arctg(\tg x)$ будет иметь форму последовательных прямых на интервалах $\left[ n\pi, (n+1)\pi \right]$, так как она повторяется с периодом $\pi$. Функция также будет нечетной, и график будет симметричен относительно начала координат.