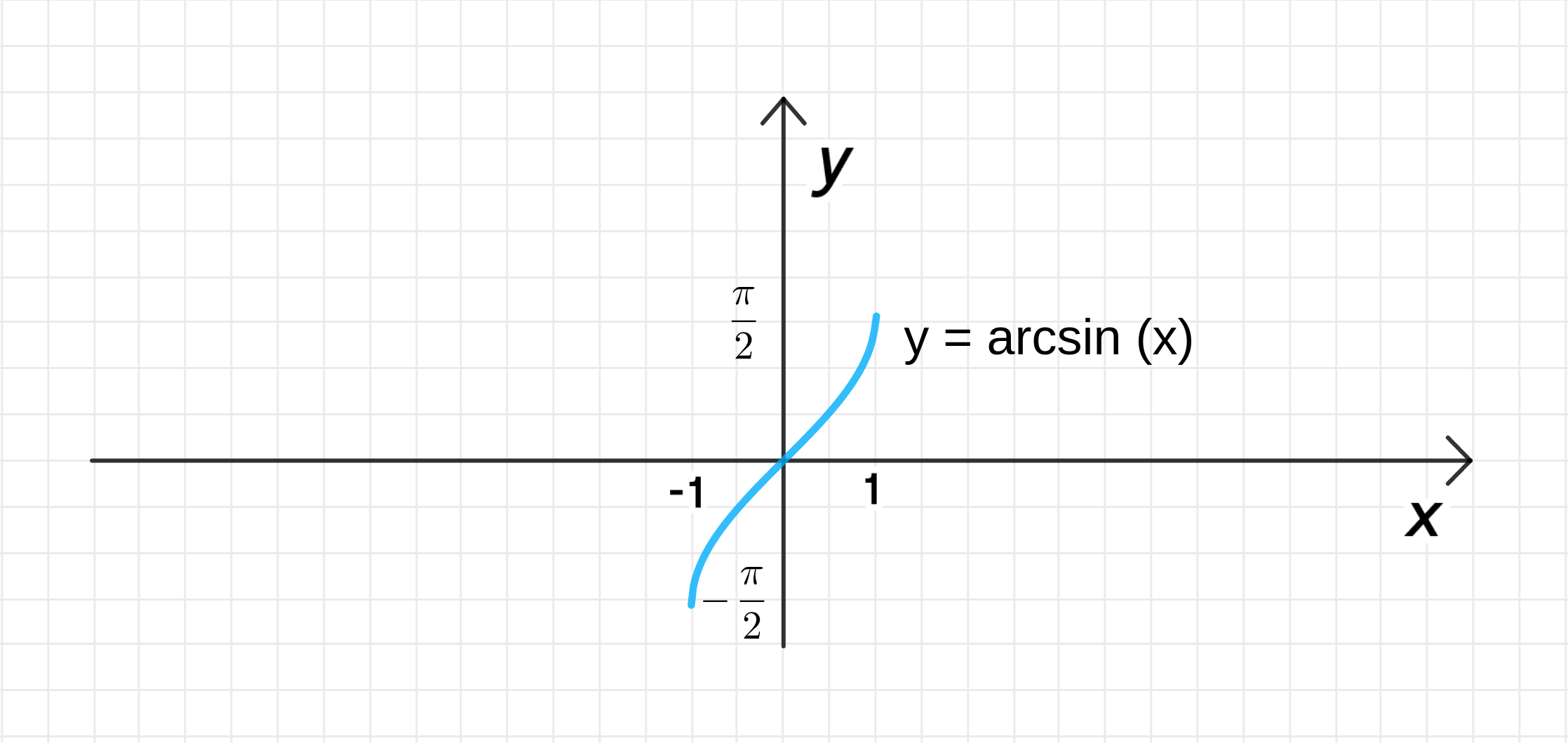ГДЗ по Алгебре 10 Класс Номер 21.7 Профильный Уровень Мордкович — Подробные Ответы

Постройте график функции:

а) у = arcsinx;

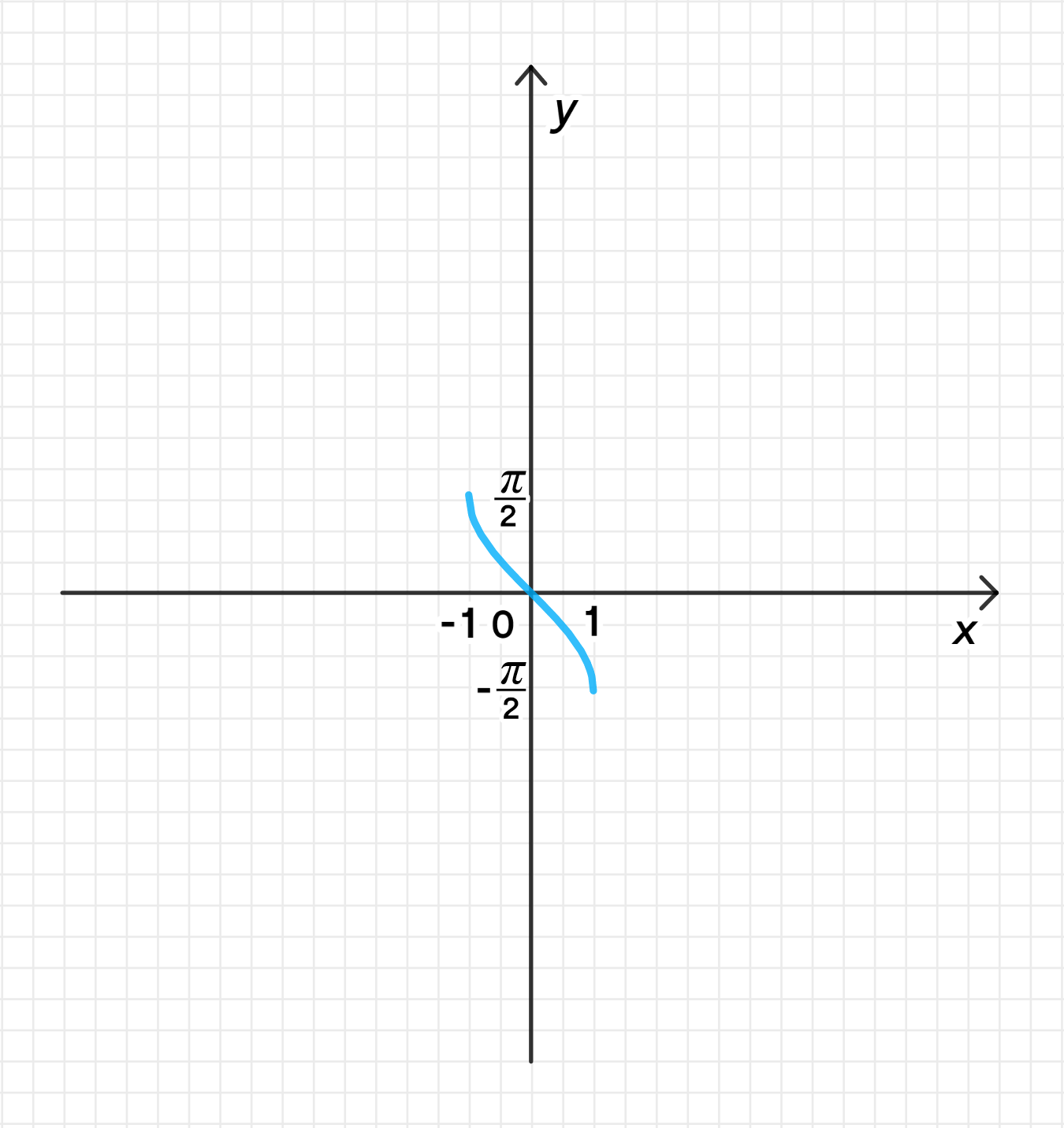
б) у = arcsin(-x);

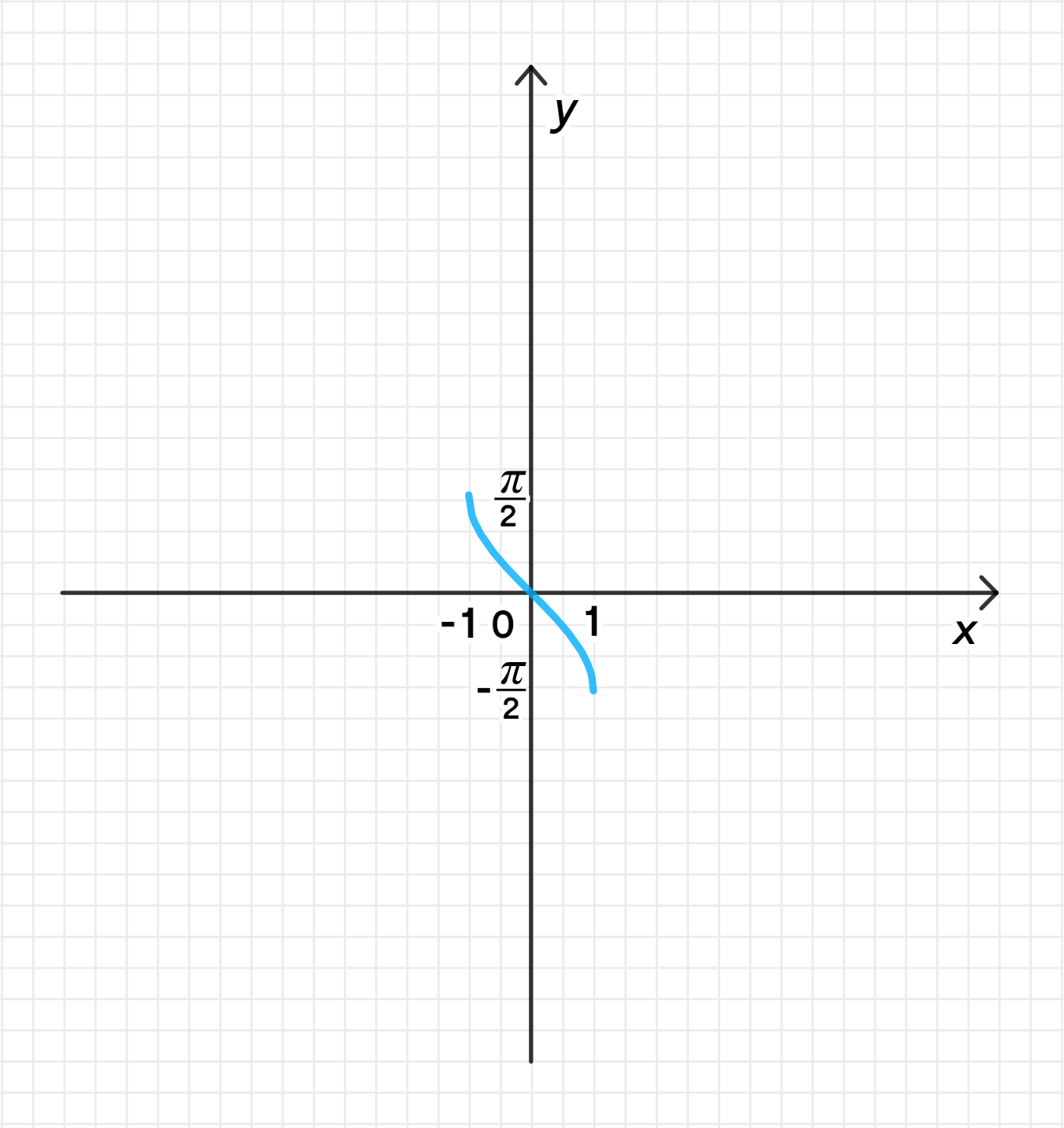
в) у = -arcsinx;

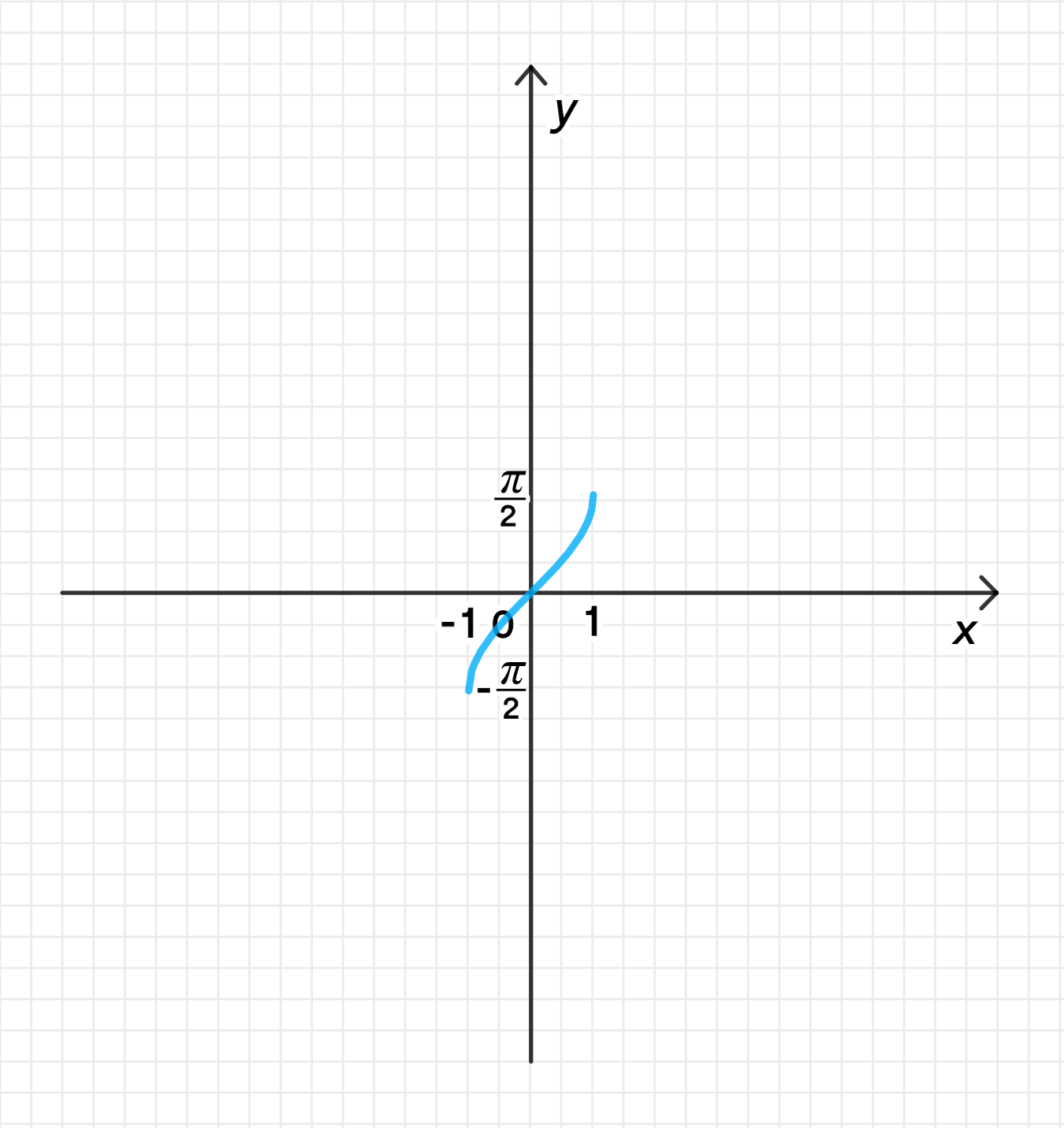
г) у = -arcsin(-x).

а) $y = \arcsin x$;

Построим график функции $y = \sin x$ на отрезке $\left[-\frac{\pi}{2}; \frac{\pi}{2}\right]$;

Отразим его относительно прямой $y = x$:

б) $y = \arcsin(-x)$;

Построим график функции $y = \arcsin x$;

Отразим его относительно оси ординат:

в) $y = -\arcsin x$;

Построим график функции $y = \arcsin x$;

Отразим его относительно оси абсцисс:

г) $y = -\arcsin(-x) = \arcsin x$;

Построим график функции $y = \sin x$ на отрезке $\left[-\frac{\pi}{2}; \frac{\pi}{2}\right]$;

Отразим его относительно прямой $y = x$:

а) $y = \arcsin x$

1) Построим график функции $y = \sin x$ на отрезке $\left[-\frac{\pi}{2}; \frac{\pi}{2}\right]$:

• Функция $y = \sin x$ является одной из основных тригонометрических функций, и её график представляет собой волну, которая повторяется с периодом $2\pi$.
• Однако нас интересует график на отрезке $\left[-\frac{\pi}{2}; \frac{\pi}{2}\right]$, то есть на промежутке от $-\frac{\pi}{2}$ до $\frac{\pi}{2}$, где синус имеет следующие ключевые значения:
  • При $x = -\frac{\pi}{2}$, $y = \sin \left(-\frac{\pi}{2}\right) = -1$
  • При $x = 0$, $y = \sin 0 = 0$
  • При $x = \frac{\pi}{2}$, $y = \sin \left(\frac{\pi}{2}\right) = 1$

Таким образом, график функции $y = \sin x$ будет представлять собой отрезок синусоиды от $(-\frac{\pi}{2}, -1)$ до $(\frac{\pi}{2}, 1)$, проходящий через точку $(0, 0)$.

2) Отразим его относительно прямой $y = x$:

• Отражение графика функции относительно прямой $y = x$ означает, что координаты каждой точки на графике меняются местами. Если на графике $y = \sin x$ для некоторой точки $(a, b)$, то после отражения эта точка перейдет в $(b, a)$.
• Таким образом, отражение графика функции $y = \sin x$ на отрезке $\left[-\frac{\pi}{2}; \frac{\pi}{2}\right]$ даст график функции $y = \arcsin x$, так как функция $\arcsin x$ является обратной функцией к $\sin x$, ограниченной на отрезке $\left[-\frac{\pi}{2}; \frac{\pi}{2}\right]$.

б) $y = \arcsin(-x)$

1) Построим график функции $y = \arcsin x$:

• Функция $y = \arcsin x$ — это обратная функция к $y = \sin x$ на отрезке $\left[-\frac{\pi}{2}; \frac{\pi}{2}\right]$.
• Значения функции $y = \arcsin x$ для $x \in \left[-1, 1\right]$ лежат в интервале $\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]$, так как:
  • $\arcsin(-1) = -\frac{\pi}{2}$
  • $\arcsin(0) = 0$
  • $\arcsin(1) = \frac{\pi}{2}$

График функции $y = \arcsin x$ — это монотонная возрастающая кривая, проходящая через начало координат и имеющая асимптоты при $x = \pm 1$.

2) Отразим его относительно оси ординат:

• Отражение относительно оси ординат меняет знак аргумента функции, то есть для функции $y = \arcsin(-x)$ мы будем рассматривать график функции $y = \arcsin x$ и заменим $x$ на $-x$.
• Это означает, что график функции $y = \arcsin(-x)$ будет зеркальным отражением графика функции $y = \arcsin x$ относительно оси $y$, то есть для каждой точки на графике $(x, y)$ на графике функции $y = \arcsin x$, мы получим точку $(-x, y)$ на графике функции $y = \arcsin(-x)$.

в) $y = -\arcsin x$

1) Построим график функции $y = \arcsin x$:

• График функции $y = \arcsin x$ мы уже построили в предыдущем пункте: это монотонная возрастающая кривая, проходящая через точку $(0, 0)$ и ограниченная значениями $\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]$ по оси $y$.

2) Отразим его относительно оси абсцисс:

• Отражение графика функции относительно оси абсцисс означает, что все значения функции меняются на противоположные. То есть, если точка на графике функции $y = \arcsin x$ имеет координаты $(x, y)$, то после отражения она будет иметь координаты $(x, -y)$.
• Таким образом, график функции $y = -\arcsin x$ будет зеркальным отражением графика функции $y = \arcsin x$ относительно оси $x$. График будет тем же, но все значения функции будут инвертированы по вертикали.

г) $y = -\arcsin(-x) = \arcsin x$

1) Построим график функции $y = \sin x$ на отрезке $\left[-\frac{\pi}{2}; \frac{\pi}{2}\right]$:

• Мы уже рассмотрели график функции $y = \sin x$ на этом отрезке. Это отрезок синусоиды, который проходит от $(-\frac{\pi}{2}, -1)$ до $(\frac{\pi}{2}, 1)$, и проходит через точку $(0, 0)$.

2) Отразим его относительно прямой $y = x$:

• Отражение графика функции $y = \sin x$ относительно прямой $y = x$ означает, что график будет преобразован в график функции $y = \arcsin x$, так как функция $y = \arcsin x$ является обратной к $y = \sin x$, ограниченной на отрезке $\left[-\frac{\pi}{2}; \frac{\pi}{2}\right]$.
• Таким образом, при отражении графика синусоиды относительно прямой $y = x$, мы получаем график функции $y = \arcsin x$.