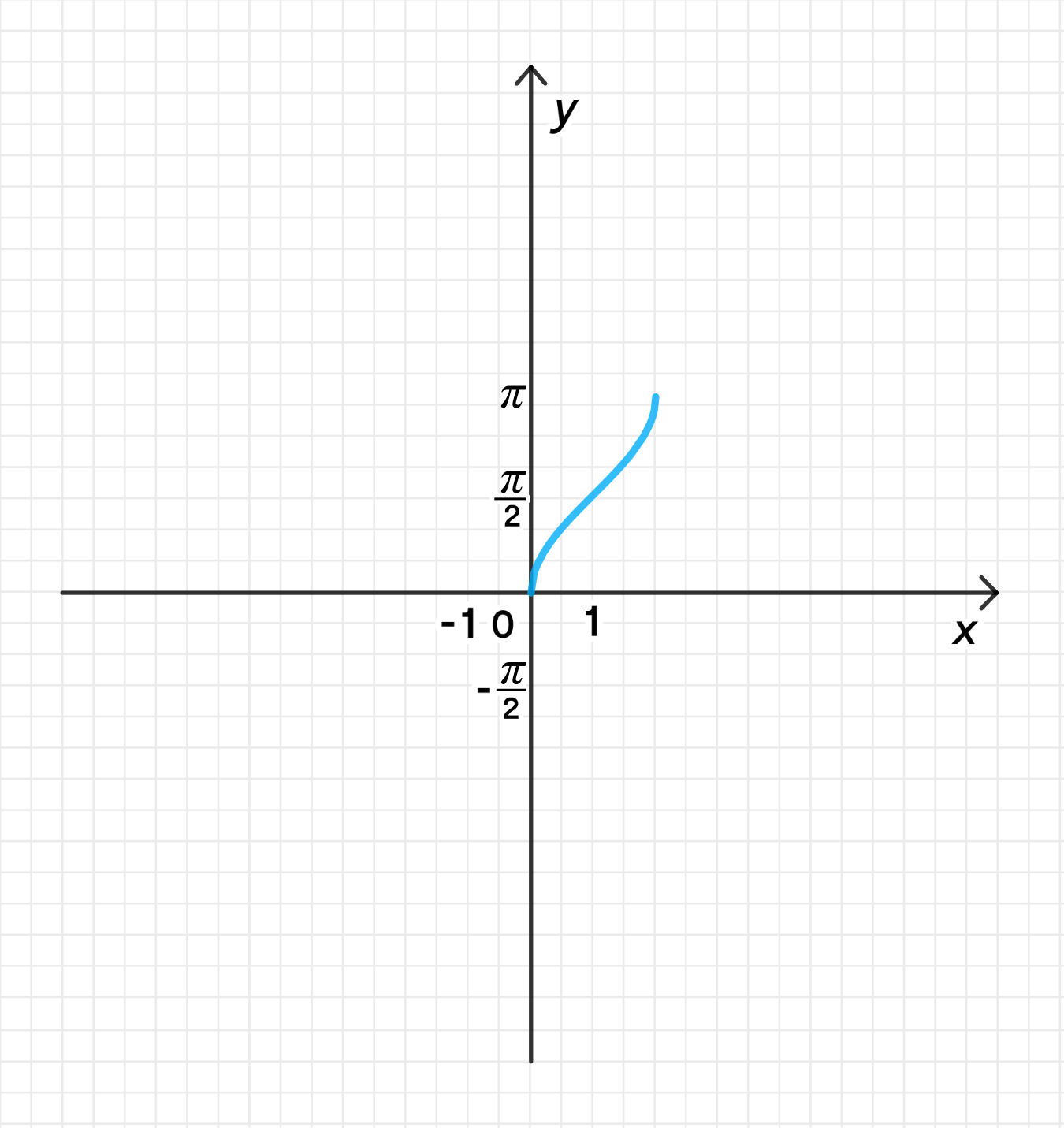ГДЗ по Алгебре 10 Класс Номер 21.8 Профильный Уровень Мордкович — Подробные Ответы

Постройте график функции:

а) $y = \arcsin(x-1) + \frac{\pi}{2}$;

б) $y = -\arcsin(x+2) — \frac{\pi}{3}$

а) $y = \arcsin(x-1) + \frac{\pi}{2}$;

Построим график функции $y = \arcsin x$;

Переместим его на 1 единицу вправо вдоль оси абсцисс;

Переместим его на $\frac{\pi}{2}$ единиц вверх вдоль оси ординат:

б) $y = -\arcsin(x+2) — \frac{\pi}{3}$;

Построим график функции $y = \arcsin x$;

Переместим его на 2 единицы влево вдоль оси абсцисс;

Отразим его относительно оси абсцисс;

Переместим его на $\frac{\pi}{3}$ единиц вниз вдоль оси ординат:

а) $y = \arcsin(x-1) + \frac{\pi}{2}$

1) Построим график функции $y = \arcsin x$:

• Функция $y = \arcsin x$ является обратной к функции $y = \sin x$, ограниченной на интервале $\left[-\frac{\pi}{2}; \frac{\pi}{2}\right]$.
• График функции $y = \arcsin x$ — это монотонная возрастающая кривая, проходящая через точки $(-1, -\frac{\pi}{2})$, $(0, 0)$, $(1, \frac{\pi}{2})$.
• График лежит в пределах интервала $x \in [-1, 1]$ и $y \in \left[-\frac{\pi}{2}, \frac{\pi}{2}\right]$.

2) Переместим его на 1 единицу вправо вдоль оси абсцисс:

• Для того чтобы переместить график на 1 единицу вправо, нужно изменить аргумент функции.
• Если у нас есть функция $y = \arcsin(x)$, то для того, чтобы сдвинуть её на 1 единицу вправо, нужно заменить $x$ на $x — 1$. То есть, функция станет $y = \arcsin(x — 1)$.
• График сдвинется на 1 единицу вправо вдоль оси абсцисс, и его новая область определения будет $x \in [0, 2]$, так как $\arcsin(x — 1)$ определена для $x \in [1, 3]$.

3) Переместим его на $\frac{\pi}{2}$ единиц вверх вдоль оси ординат:

• Для того чтобы переместить график вверх, нужно просто прибавить к функции постоянную величину.
• Если у нас есть функция $y = \arcsin(x — 1)$, то чтобы сдвинуть её на $\frac{\pi}{2}$ единиц вверх, нужно прибавить $\frac{\pi}{2}$. То есть, функция становится $y = \arcsin(x — 1) + \frac{\pi}{2}$.
• Это означает, что все значения функции на графике увеличиваются на $\frac{\pi}{2}$, и новый диапазон значений функции будет $y \in \left[\frac{\pi}{2}, \frac{3\pi}{2}\right]$.

б) $y = -\arcsin(x+2) — \frac{\pi}{3}$

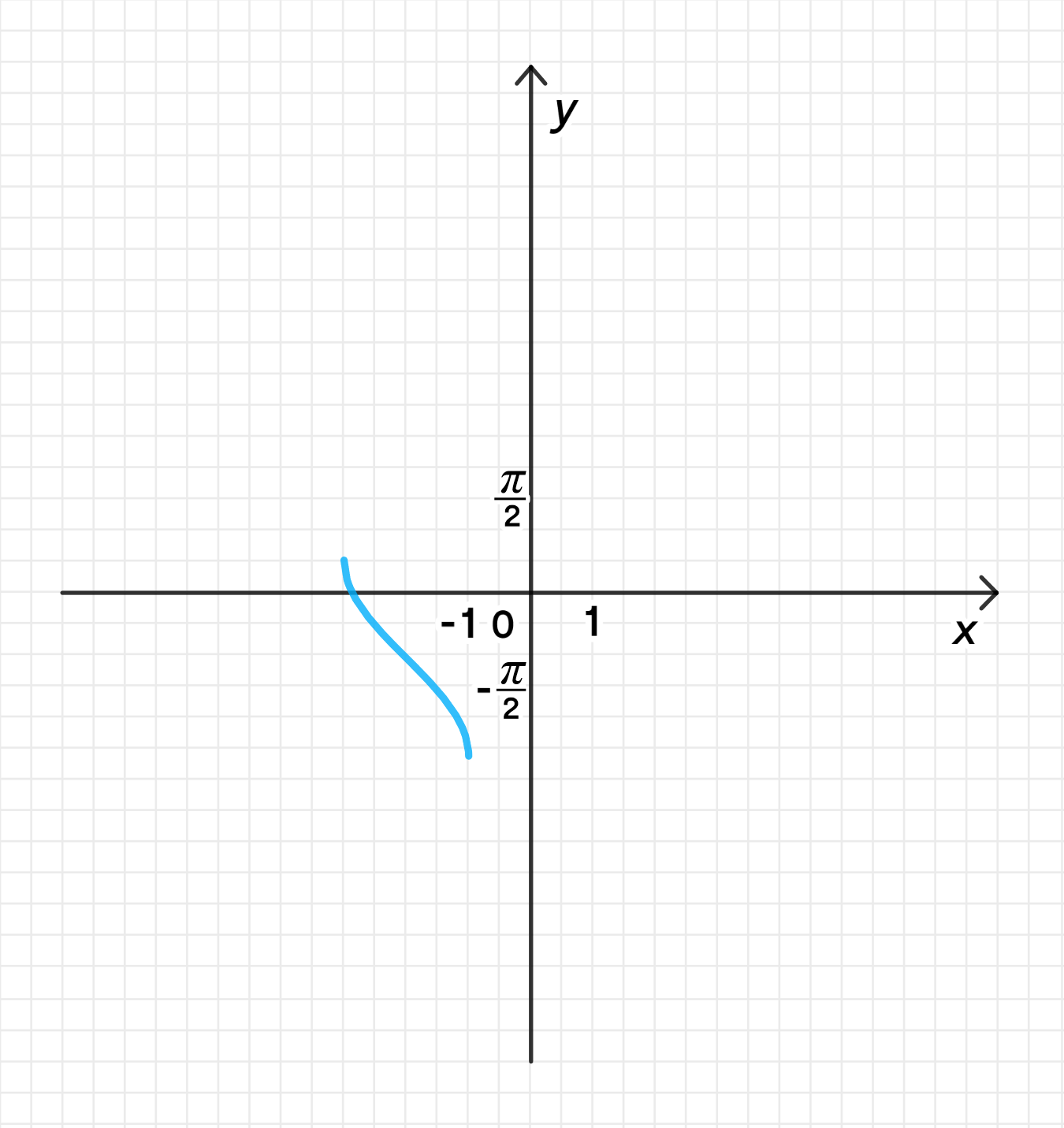
1) Построим график функции $y = \arcsin x$:

• Как и в первом пункте, строим график функции $y = \arcsin x$, который будет монотонной возрастающей кривой от $(-1, -\frac{\pi}{2})$ до $(1, \frac{\pi}{2})$.

2) Переместим его на 2 единицы влево вдоль оси абсцисс:

• Чтобы переместить график на 2 единицы влево, нужно изменить аргумент функции.
• Если у нас есть функция $y = \arcsin(x)$, то для того, чтобы сдвинуть её на 2 единицы влево, заменяем $x$ на $x + 2$. То есть функция становится $y = \arcsin(x + 2)$.
• Это сдвинет график на 2 единицы влево вдоль оси абсцисс, и область определения функции будет $x \in [-3, -1]$.

3) Отразим его относительно оси абсцисс:

• Отражение функции относительно оси абсцисс означает, что все значения функции меняются на противоположные.
• Если у нас есть график функции $y = \arcsin(x + 2)$, то его отражение относительно оси абсцисс будет $y = -\arcsin(x + 2)$.
• Это инвертирует все значения функции по вертикали, и график будет зеркальным отражением исходного.

4) Переместим его на $\frac{\pi}{3}$ единиц вниз вдоль оси ординат:

• Для того чтобы переместить график вниз, нужно вычесть из функции постоянную величину.
• Если у нас есть функция $y = -\arcsin(x + 2)$, то чтобы сдвинуть её на $\frac{\pi}{3}$ единиц вниз, нужно вычесть $\frac{\pi}{3}$. То есть, функция станет $y = -\arcsin(x + 2) — \frac{\pi}{3}$.
• Это означает, что все значения функции на графике уменьшатся на $\frac{\pi}{3}$, и новый диапазон значений функции будет $y \in \left[-\frac{\pi}{2} — \frac{\pi}{3}, \frac{\pi}{2} — \frac{\pi}{3}\right]$.