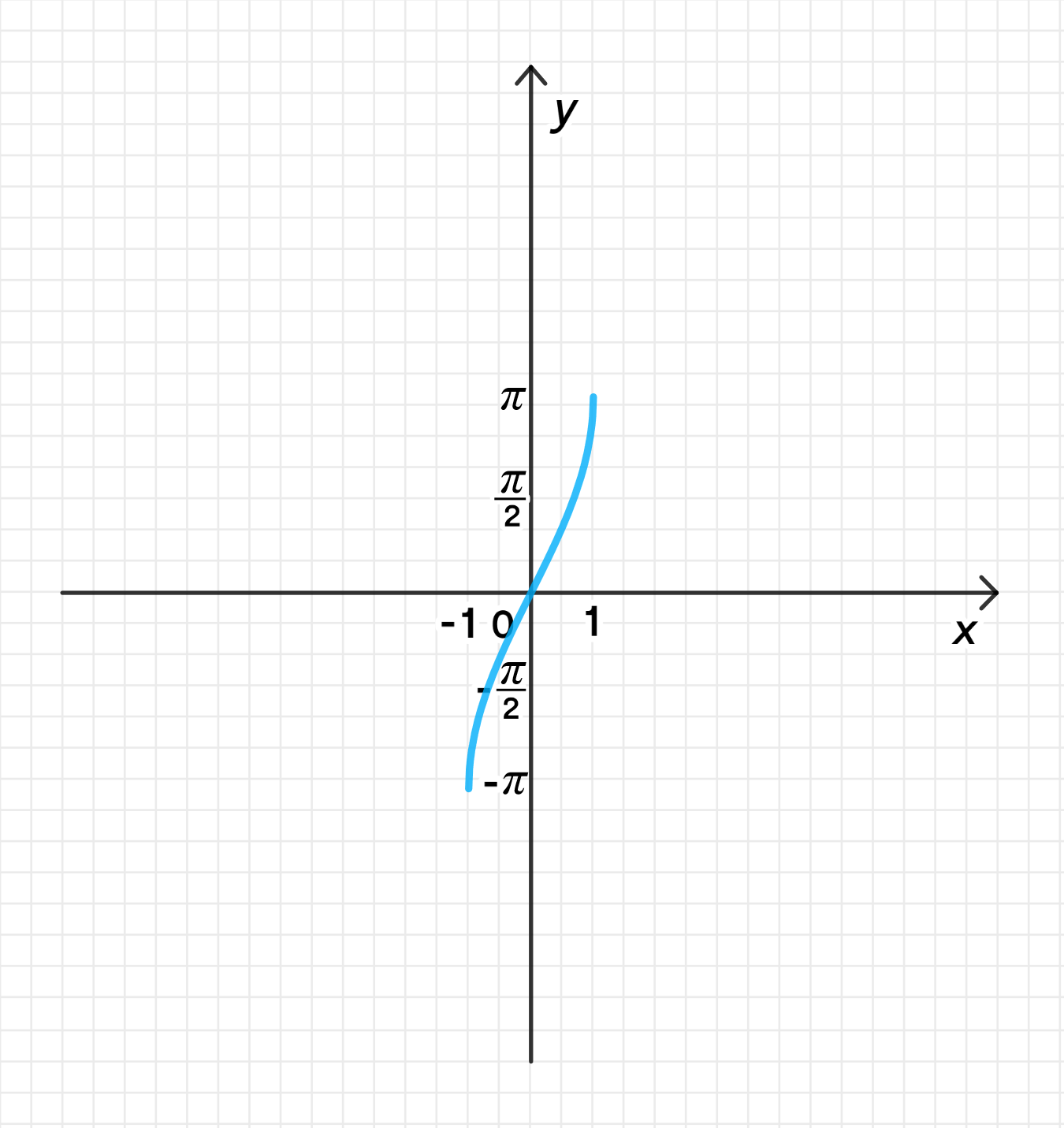ГДЗ по Алгебре 10 Класс Номер 21.9 Профильный Уровень Мордкович — Подробные Ответы

Постройте график функции:

а) $y = 2 \arcsin x$;

б) $y = \frac{\pi}{3} — \arcsin x$;

в) $y = -\frac{1}{3} \arcsin x$;

г) $y = -2 \arcsin(x — 3)$

а) $y = 2 \arcsin x$;

Построим график функции $y = \arcsin x$;

Растянем его от оси $Ox$ с коэффициентом $k = 2$.

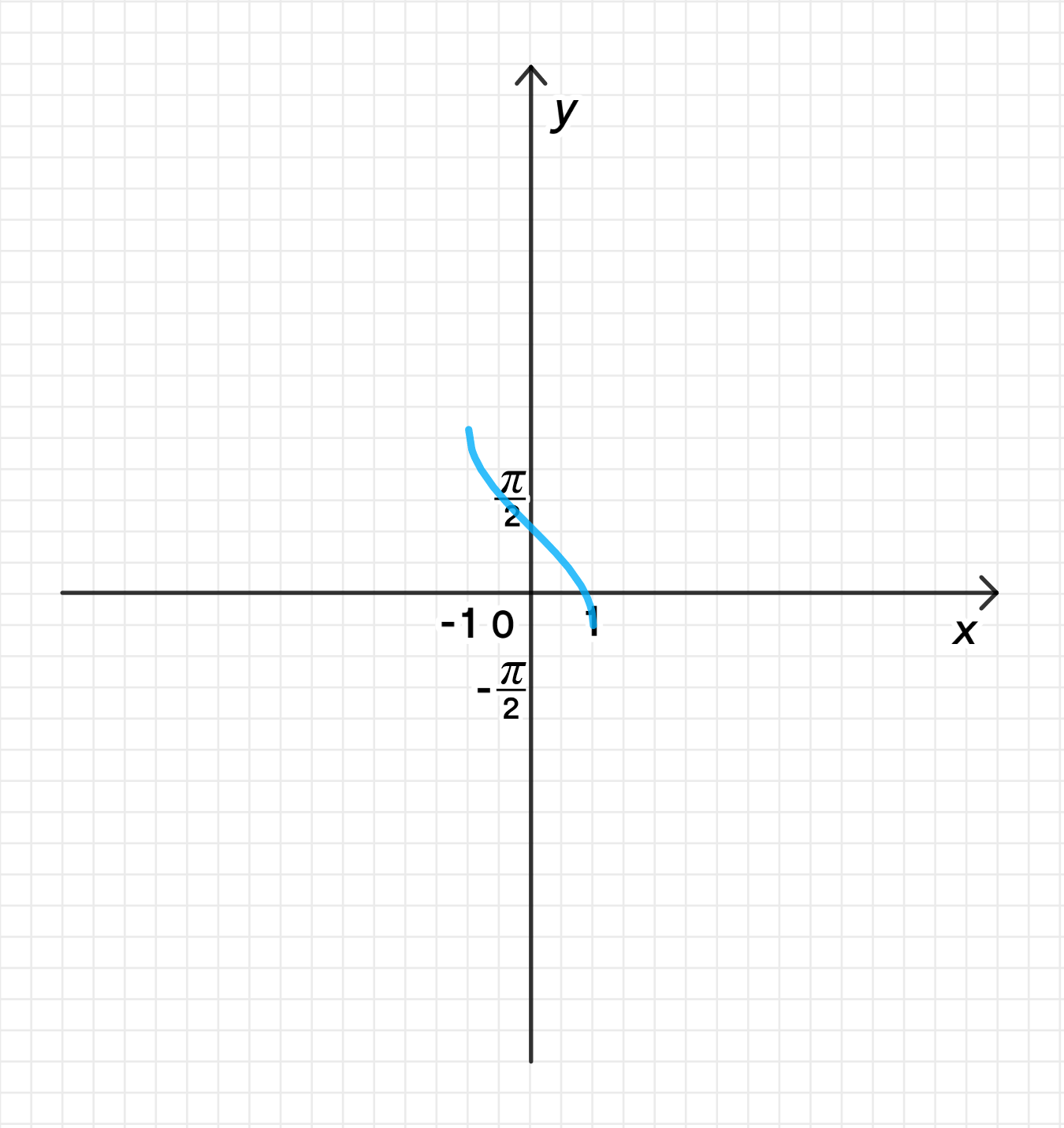
б) $y = \frac{\pi}{3} — \arcsin x$;

Построим график функции $y = \arcsin x$;

Отразим его относительно оси абсцисс;

Переместим его на $\frac{\pi}{3}$ единиц вверх вдоль оси ординат.

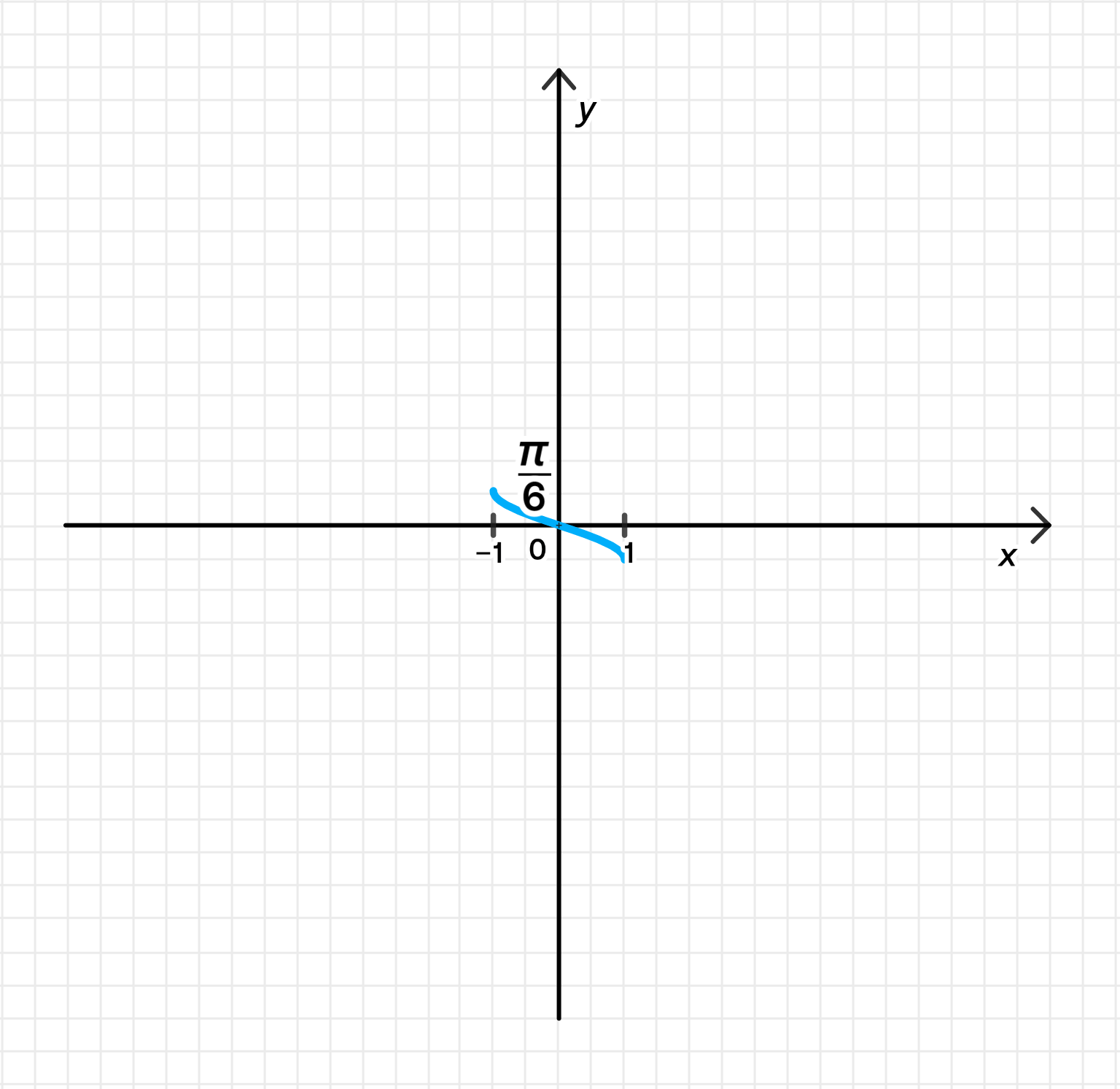
в) $y = -\frac{1}{3} \arcsin x$;

Построим график функции $y = \arcsin x$;

Отразим его относительно оси абсцисс;

Сожмем его к оси $Ox$ с коэффициентом $k = 3$.

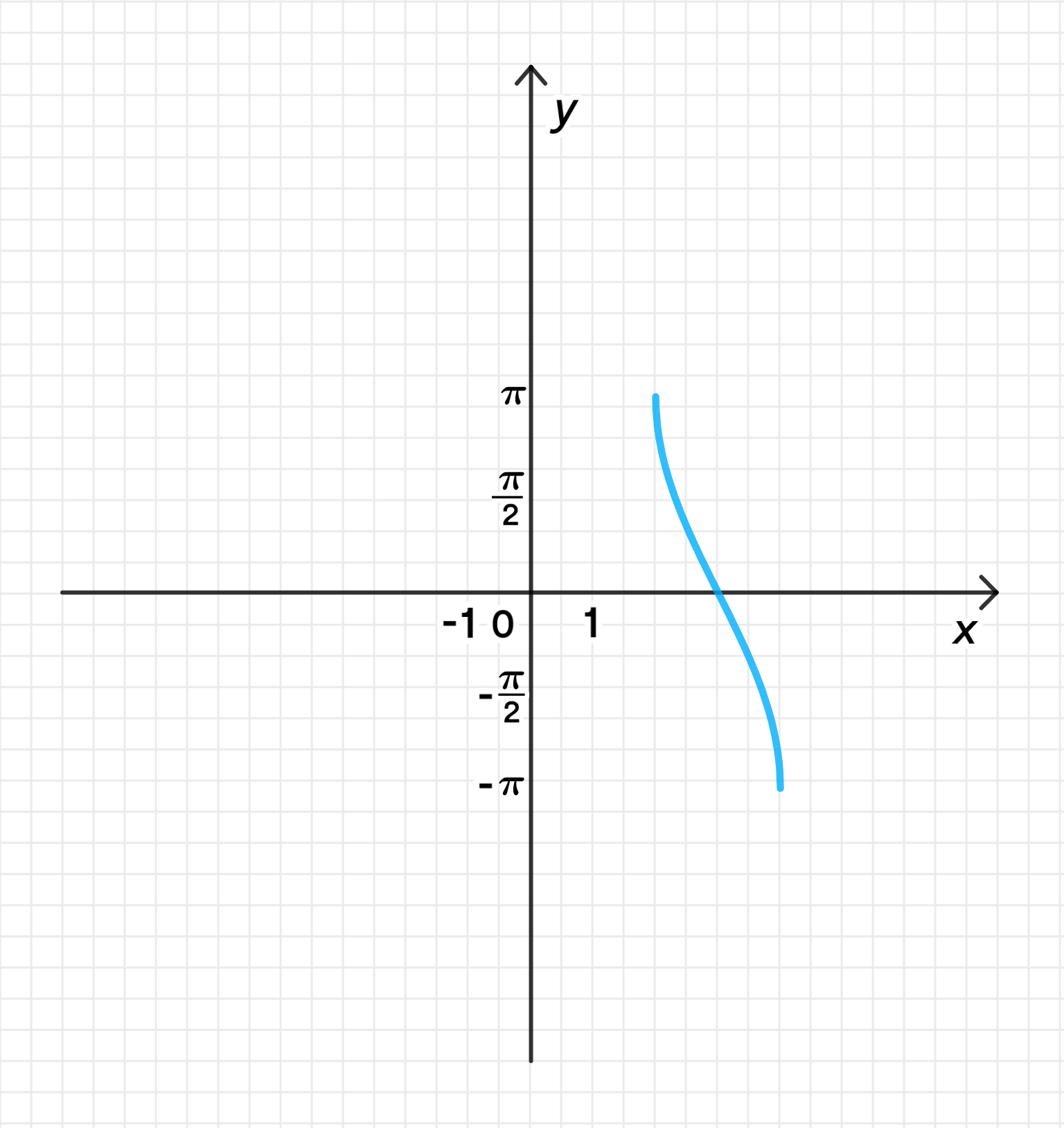
г) $y = -2 \arcsin(x — 3)$;

Построим график функции $y = \arcsin x$;

Переместим его на 3 единицы вправо вдоль оси абсцисс;

Отразим его относительно оси абсцисс;

Растянем его от оси $Ox$ с коэффициентом $k = 2$.

Для начала уточним, что функция $y = \arcsin x$ определена на интервале $-1 \leq x \leq 1$, и её график представляет собой гладкую кривую, которая возрастает от $y = -\frac{\pi}{2}$ при $x = -1$ до $y = \frac{\pi}{2}$ при $x = 1$.

а) $y = 2 \arcsin x$

Шаг 1: Построим график функции $y = \arcsin x$.

График функции $y = \arcsin x$ представляет собой кривую, которая:

• Начинается в точке $(-1, -\frac{\pi}{2})$,
• Проходит через точку $(0, 0)$,
• Заканчивается в точке $(1, \frac{\pi}{2})$.

Шаг 2: Растянем график вдоль оси $Ox$ с коэффициентом $k = 2$.

Когда мы умножаем функцию на 2, это означает растяжение графика вдоль оси ординат. В данной ситуации значения функции увеличиваются в два раза. Таким образом, мы будем иметь:

• $y = 2 \times (-\frac{\pi}{2}) = -\pi$ при $x = -1$,
• $y = 2 \times 0 = 0$ при $x = 0$,
• $y = 2 \times \frac{\pi}{2} = \pi$ при $x = 1$.

График будет также гладким, но теперь значения функции будут в два раза больше.

б) $y = \frac{\pi}{3} — \arcsin x$

Шаг 1: Построим график функции $y = \arcsin x$.

Сначала строим тот же график функции $y = \arcsin x$, как описано выше.

Шаг 2: Отразим график относительно оси абсцисс.

Отражение функции относительно оси абсцисс означает, что все её значения изменят знак. То есть, функция $y = \arcsin x$ превратится в $y = -\arcsin x$. Это отразит график по вертикали. Например:

• $y = -\frac{\pi}{2}$ при $x = -1$,
• $y = 0$ при $x = 0$,
• $y = \frac{\pi}{2}$ при $x = 1$.

Шаг 3: Переместим график на $\frac{\pi}{3}$ единиц вверх вдоль оси ординат.

Перемещение графика на $\frac{\pi}{3}$ единиц вверх означает, что мы добавляем $\frac{\pi}{3}$ ко всем значениям функции. Получаем:

• $y = -\frac{\pi}{2} + \frac{\pi}{3} = -\frac{\pi}{6}$ при $x = -1$,
• $y = 0 + \frac{\pi}{3} = \frac{\pi}{3}$ при $x = 0$,
• $y = \frac{\pi}{2} + \frac{\pi}{3} = \frac{5\pi}{6}$ при $x = 1$.

График будет смещён вверх на $\frac{\pi}{3}$, с отражением относительно оси абсцисс.

в) $y = -\frac{1}{3} \arcsin x$

Шаг 1: Построим график функции $y = \arcsin x$.

Построим исходный график функции $y = \arcsin x$ как описано ранее.

Шаг 2: Отразим график относительно оси абсцисс.

Отражение функции относительно оси абсцисс даёт $y = -\arcsin x$, как в предыдущем пункте. Таким образом, значения функции будут отрицательными.

Шаг 3: Сожмем график к оси $Ox$ с коэффициентом $k = 3$.

Когда мы умножаем функцию на $-\frac{1}{3}$, это означает сжатие графика вдоль оси ординат на коэффициент 3. То есть для каждого значения $x$ результат функции $y$ уменьшится в три раза и станет отрицательным:

• $y = -\frac{1}{3} \times (-\frac{\pi}{2}) = \frac{\pi}{6}$ при $x = -1$,
• $y = -\frac{1}{3} \times 0 = 0$ при $x = 0$,
• $y = -\frac{1}{3} \times \frac{\pi}{2} = -\frac{\pi}{6}$ при $x = 1$.

График будет сжат вдоль оси $Ox$ и отражён относительно оси абсцисс.

г) $y = -2 \arcsin(x — 3)$

Шаг 1: Построим график функции $y = \arcsin x$.

Сначала строим исходный график функции $y = \arcsin x$.

Шаг 2: Переместим график на 3 единицы вправо вдоль оси абсцисс.

Когда аргумент функции сдвигается на $-3$, это означает, что график сдвигается на 3 единицы вправо. То есть:

• Точка $x = -1$ теперь будет находиться в точке $x = 2$,
• Точка $x = 0$ теперь будет находиться в точке $x = 3$,
• Точка $x = 1$ теперь будет находиться в точке $x = 4$.

Шаг 3: Отразим график относительно оси абсцисс.

Отражение графика функции $y = \arcsin(x — 3)$ относительно оси абсцисс даст нам $y = -\arcsin(x — 3)$, как в предыдущих пунктах.

Шаг 4: Растянем график вдоль оси $Ox$ с коэффициентом $k = 2$.

Умножение функции на 2 растягивает её значения вдоль оси ординат. Таким образом:

• $y = -2 \times (-\frac{\pi}{2}) = \pi$ при $x = 2$,
• $y = -2 \times 0 = 0$ при $x = 3$,
• $y = -2 \times \frac{\pi}{2} = -\pi$ при $x = 4$.