ГДЗ по Алгебре 10 Класс Номер 22.23 Профильный Уровень Мордкович — Подробные Ответы

Сколько корней имеет заданное уравнение на заданном промежутке:

а) $\cos x = \frac{1}{3}, \, x \in [1; 6]$;

б) $\cos x = -0.4, \, x \in [3; 11]$

Сколько корней имеет заданное уравнение на заданном промежутке:

а) $\cos x = \frac{1}{3}, \, x \in [1; 6]$;

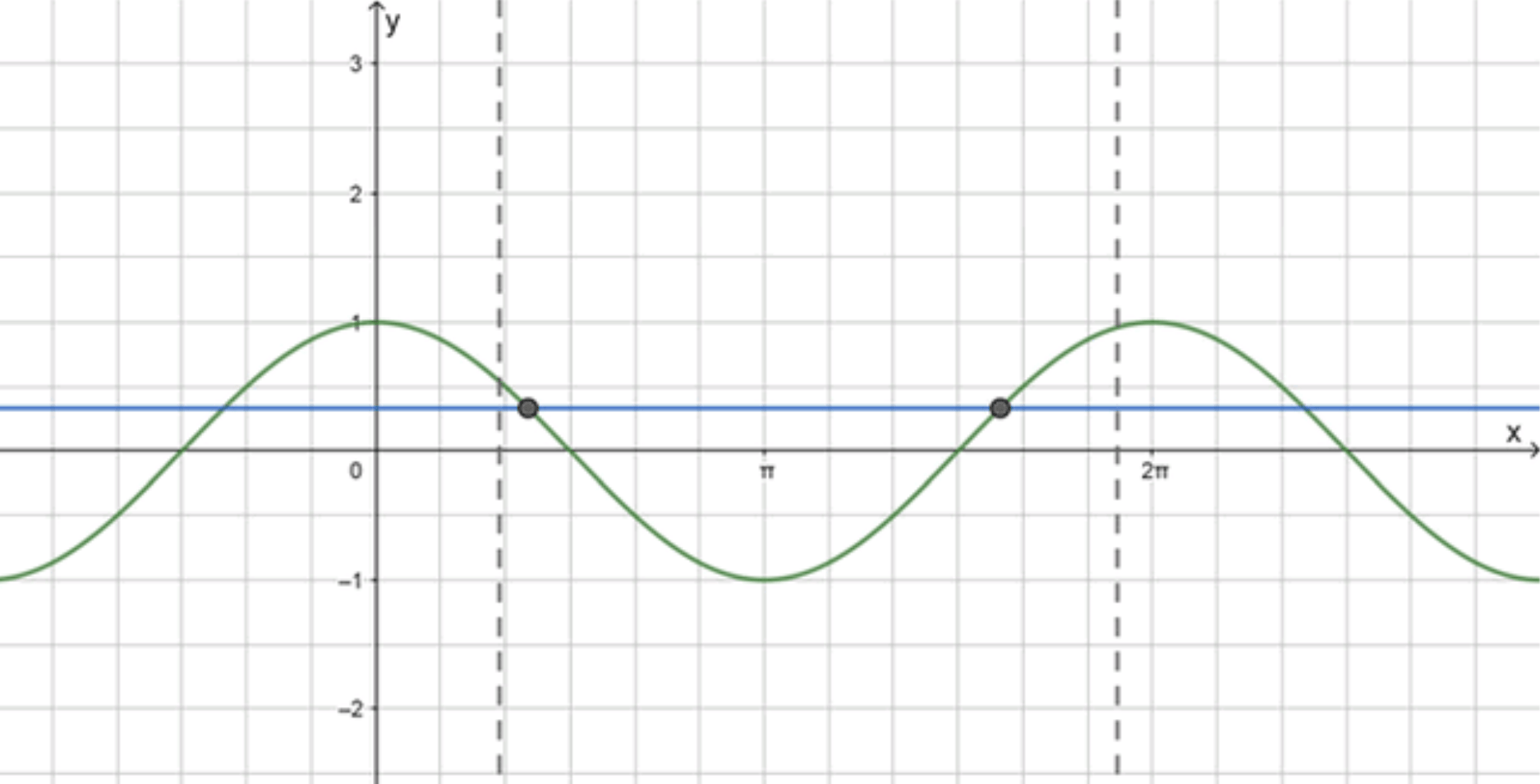
Построим графики функций $y = \cos x$ и $y = \frac{1}{3}$:

На данном отрезке графики пересекаются в двух точках;

Ответ: 2.

б) $\cos x = -0.4, \, x \in [3; 11]$;

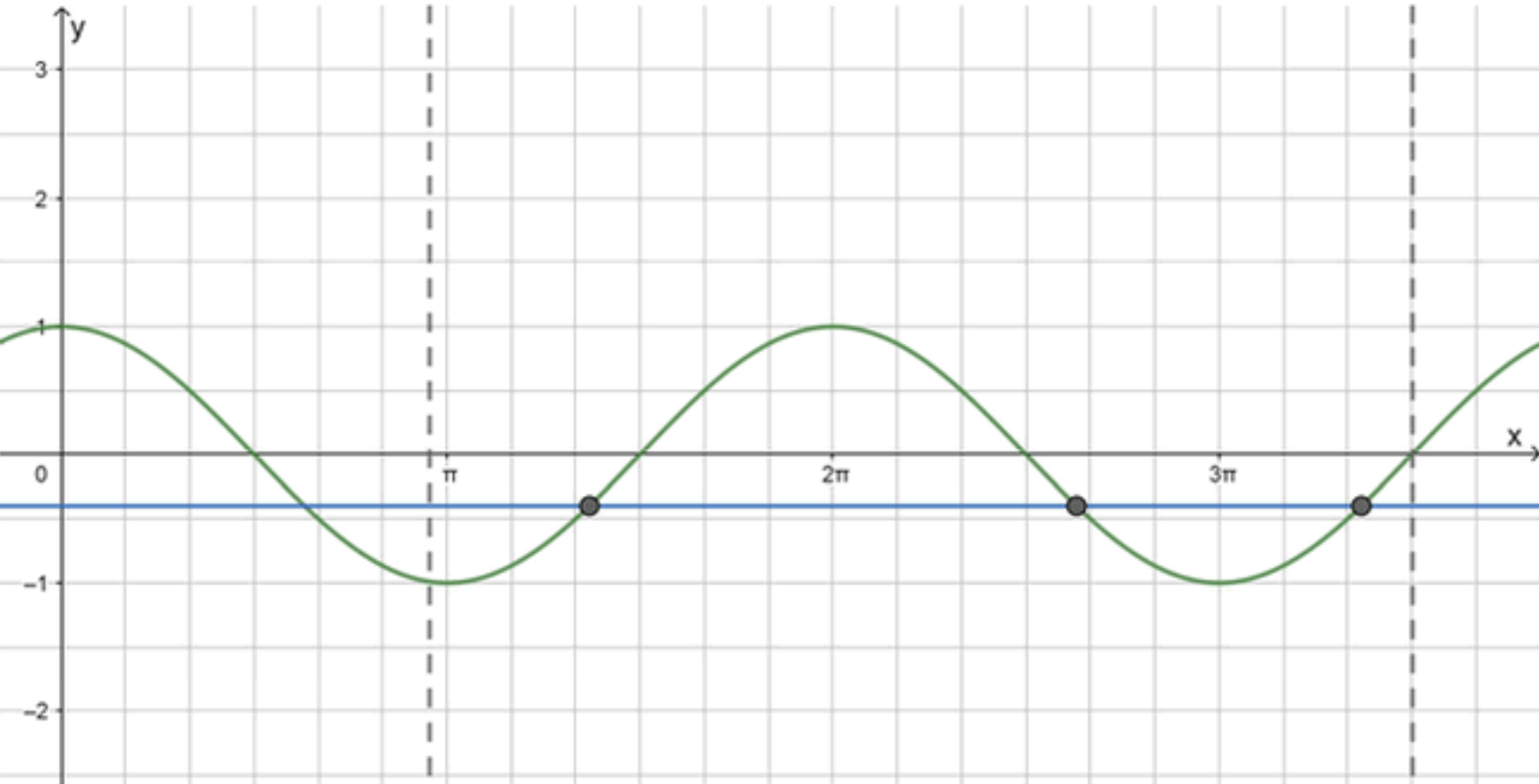
Построим графики функций $y = \cos x$ и $y = -0.4$:

На данном отрезке графики пересекаются в трех точках;

Ответ: 3.

а) $\cos x = \frac{1}{3}, \, x \in [1; 6]$

Шаг 1: Анализ уравнения

Рассмотрим уравнение $\cos x = \frac{1}{3}$. Для поиска количества корней на отрезке $x \in [1; 6]$, нужно понять, где график функции $y = \cos x$ пересекается с прямой $y = \frac{1}{3}$ на данном промежутке.

График функции $y = \cos x$ — это периодическая волна с периодом $2\pi$, колеблющаяся от -1 до 1.

Прямая $y = \frac{1}{3}$ — горизонтальная линия, которая лежит между -1 и 1 на оси $y$, и она будет пересекать график функции $y = \cos x$ в двух точках на одном периоде.

Шаг 2: Определяем количество корней

График функции $y = \cos x$ пересекает горизонтальную линию $y = \frac{1}{3}$ дважды за один период $[0; 2\pi]$. Период функции $\cos x$ равен $2\pi$, и на отрезке $[1; 6]$ помещается полный период.

Функция $y = \cos x$ пересечет прямую $y = \frac{1}{3}$ дважды на промежутке от $x = 1$ до $x = 6$.

Шаг 3: Вычисление точных корней

Чтобы вычислить точные значения этих корней, найдем значение $x$, при котором $\cos x = \frac{1}{3}$.

Используем обратную функцию косинуса:

$$x_1 = \arccos \left( \frac{1}{3} \right)$$

Это дает нам первую точку пересечения. Поскольку косинус — это периодическая функция, вторая точка пересечения будет находиться через период $2\pi$, то есть:

$$x_2 = 2\pi — \arccos \left( \frac{1}{3} \right)$$

На отрезке $x \in [1; 6]$ эти два значения $x_1$ и $x_2$ лежат между 1 и 6.

Шаг 4: Ответ

График функции $y = \cos x$ и горизонтальная линия $y = \frac{1}{3}$ пересекаются в двух точках на отрезке $x \in [1; 6]$.

Ответ: 2.

б) $\cos x = -0.4, \, x \in [3; 11]$

Шаг 1: Анализ уравнения

Рассмотрим уравнение $\cos x = -0.4$. Здесь мы ищем пересечение графика функции $y = \cos x$ с горизонтальной линией $y = -0.4$ на отрезке $x \in [3; 11]$.

График функции $y = \cos x$ снова представляет собой периодическую волну, которая колеблется от -1 до 1. Горизонтальная линия $y = -0.4$ пересекает график дважды за каждый период $2\pi$.

Шаг 2: Определяем количество корней

Период функции $y = \cos x$ равен $2\pi$, и на отрезке $[3; 11]$ помещается два периода (примерно от $3$ до $11$).

1. Первый период будет лежать на отрезке $[3; 3 + 2\pi]$, а второй — на отрезке $[3 + 2\pi; 3 + 4\pi]$.
2. На каждом периоде график функции пересекает прямую $y = -0.4$ дважды.

Следовательно, на отрезке $[3; 11]$ будет 4 пересечения графика с прямой.

Шаг 3: Вычисление точных корней

Для нахождения точных корней используем обратную функцию косинуса:

$$x_1 = \arccos(-0.4)$$

Это даст первую точку пересечения. Вторая точка пересечения будет находиться на том же периоде, то есть:

$$x_2 = 2\pi — \arccos(-0.4)$$

Эти два корня лежат в пределах первого периода. Повторяем это для второго периода:

$$x_3 = 2\pi + \arccos(-0.4)$$ $$x_4 = 2\pi + (2\pi — \arccos(-0.4))$$

Шаг 4: Ответ

График функции $y = \cos x$ и горизонтальная линия $y = -0.4$ пересекаются в четырех точках на отрезке $x \in [3; 11]$.

Ответ: 3.