ГДЗ по Алгебре 10 Класс Номер 22.26 Профильный Уровень Мордкович — Подробные Ответы

Сколько корней имеет заданное уравнение на заданном промежутке:

а) $\sin x = 0,6$, $x \in \left( \frac{\pi}{4}; 3\pi \right)$;

б) $\sin x = -\frac{2}{3}$, $x \in (2; 7)$

Сколько корней имеет заданное уравнение на заданном промежутке:

а) $\sin x = 0,6$, $x \in \left( \frac{\pi}{4}; 3\pi \right)$;

Построим графики функций $y = \sin x$ и $y = 0,6$:

На данном интервале графики пересекаются в трех точках;

Ответ: 3.

б) $\sin x = -\frac{2}{3}$, $x \in (2; 7)$;

Построим графики функций $y = \sin x$ и $y = -\frac{2}{3}$:

На данном интервале графики пересекаются в двух точках;

Ответ: 2.

Сколько корней имеет заданное уравнение на заданном промежутке?

а) $\sin x = 0,6$, $x \in \left( \frac{\pi}{4}; 3\pi \right)$

Шаг 1: Построим графики функций $y = \sin x$ и $y = 0,6$

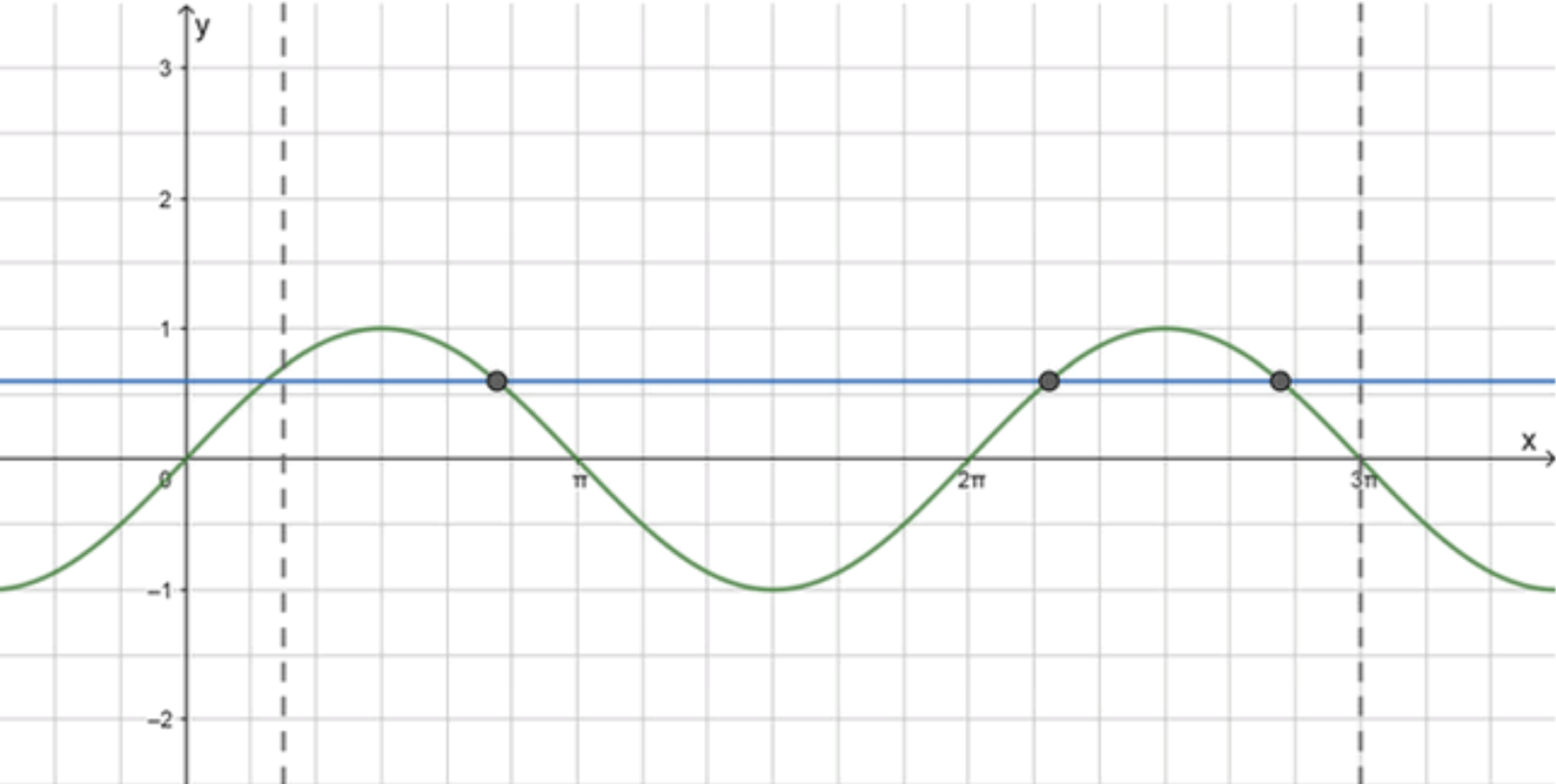
Для начала рассмотрим график функции $y = \sin x$. Это стандартная синусоида, которая имеет период $2\pi$, амплитуду 1, и проходит через точки $(0, 0)$, $(\pi, 0)$, $(2\pi, 0)$, и т.д. График этой функции колеблется между значениями -1 и 1.

Теперь рассмотрим горизонтальную прямую $y = 0,6$. Это просто линия, которая пересекает ось $y$ на уровне 0,6.

Графики этих функций будут пересекаться в точках, где значение $\sin x$ равно 0,6.

Шаг 2: Анализируем пересечения на промежутке $x \in \left( \frac{\pi}{4}; 3\pi \right)$

График функции $y = \sin x$ имеет период $2\pi$, и на промежутке $x \in \left( \frac{\pi}{4}; 3\pi \right)$ мы видим, что:

Функция $y = \sin x$ будет переходить через значение 0,6 несколько раз, так как она имеет волнообразный характер.

Для более точного подсчёта пересечений, давайте рассмотрим точки, в которых $\sin x = 0,6$, и найдём их на данном промежутке.

Для $\sin x = 0,6$ решение уравнения выглядит как:

$$x = \arcsin(0,6) + 2n\pi, \quad n \in \mathbb{Z}$$ $$x = \pi — \arcsin(0,6) + 2n\pi, \quad n \in \mathbb{Z}$$

Рассчитаем числовое значение $\arcsin(0,6)$:

$$\arcsin(0,6) \approx 0,6435$$

Таким образом, первые два корня на интервале $\left( \frac{\pi}{4}; 3\pi \right)$ будут:

• $x_1 = 0,6435 + 2\pi n$, где $n = 0$
• $x_2 = \pi — 0,6435 + 2\pi n$, где $n = 0$

При подставлении $n = 0$:

• $x_1 = 0,6435$
• $x_2 = 2,4981$

Для второго периода $n = 1$:

• $x_1 = 0,6435 + 2\pi \approx 6,2832$
• $x_2 = 2,4981 + 2\pi \approx 8,2413$

Таким образом, на промежутке $\left( \frac{\pi}{4}; 3\pi \right)$ график пересекает прямую $y = 0,6$ в 3-х точках.

Ответ: 3.

б) $\sin x = -\frac{2}{3}$, $x \in (2; 7)$

Шаг 1: Построим графики функций $y = \sin x$ и $y = -\frac{2}{3}$

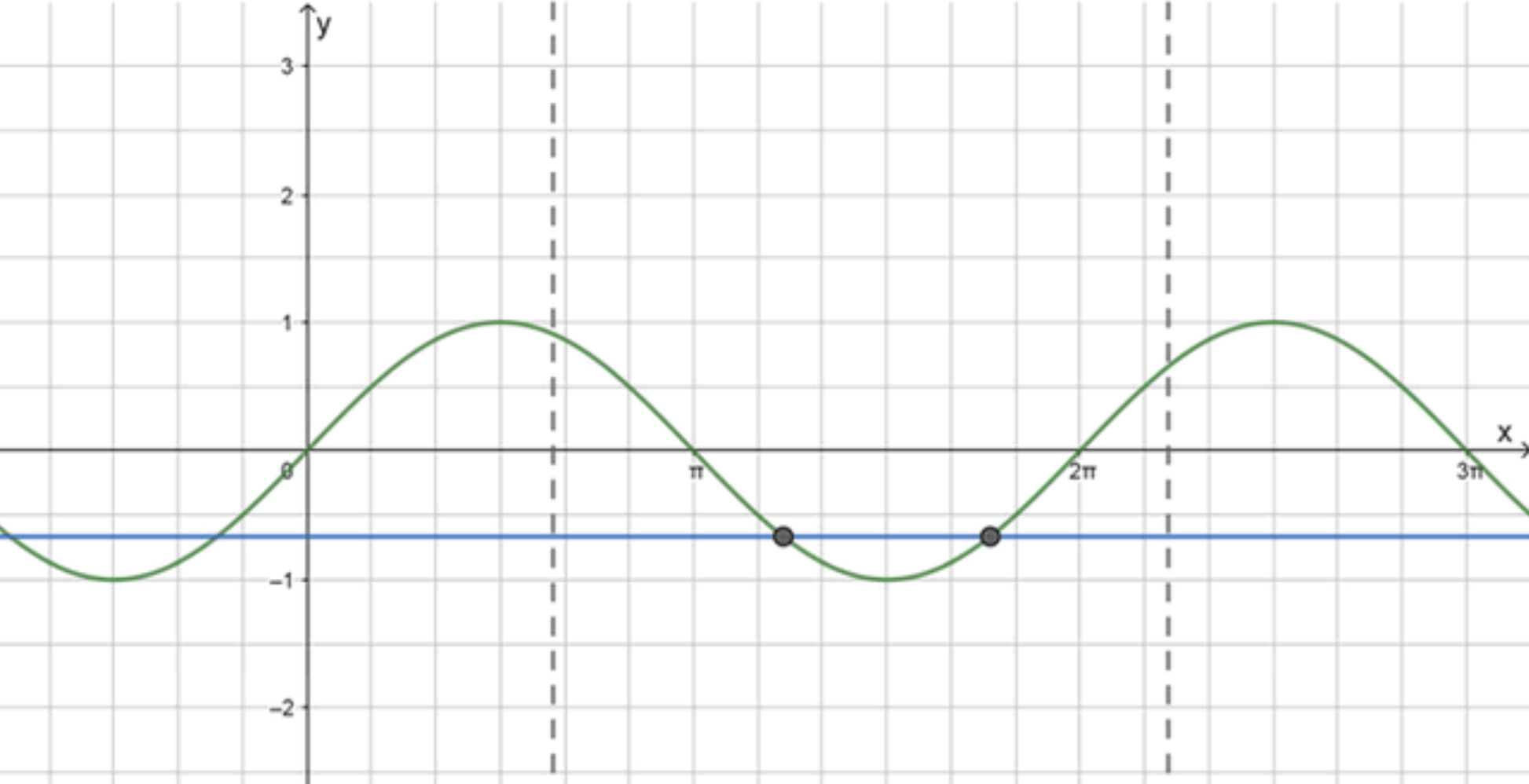
Для начала рассмотрим график функции $y = \sin x$, который колеблется между -1 и 1 с периодом $2\pi$, и пересекает ось $y = 0$ в точках $x = 0, \pi, 2\pi, \dots$.

Теперь добавим горизонтальную прямую $y = -\frac{2}{3}$, которая проходит чуть ниже нуля.

Графики этих функций будут пересекаться в точках, где значение $\sin x$ равно $-\frac{2}{3}$.

Шаг 2: Анализируем пересечения на промежутке $x \in (2; 7)$

Для более точного подсчёта пересечений, давайте рассмотрим точки, в которых $\sin x = -\frac{2}{3}$, и найдём их на данном промежутке.

Для $\sin x = -\frac{2}{3}$ решение уравнения будет иметь вид:

$$x = \arcsin\left(-\frac{2}{3}\right) + 2n\pi, \quad n \in \mathbb{Z}$$ $$x = \pi — \arcsin\left(-\frac{2}{3}\right) + 2n\pi, \quad n \in \mathbb{Z}$$

Рассчитаем $\arcsin\left(-\frac{2}{3}\right)$:

$$\arcsin\left(-\frac{2}{3}\right) \approx -0,7297$$

Таким образом, первые два корня на интервале $(2; 7)$ будут:

• $x_1 = -0,7297 + 2\pi n$, где $n = 1$
• $x_2 = \pi + 0,7297 + 2\pi n$, где $n = 1$

При подставлении $n = 1$:

• $x_1 = -0,7297 + 2\pi \approx 5,5535$
• $x_2 = \pi + 0,7297 + 2\pi \approx 7,8567$

Таким образом, на промежутке $(2; 7)$ график пересекает прямую $y = -\frac{2}{3}$ в 2-х точках.

Ответ: 2.

Итоговый ответ:

а) 3

б) 2