ГДЗ по Алгебре 10 Класс Номер 25.24 Профильный Уровень Мордкович — Подробные Ответы

Точка К — середина стороны CD квадрата ABCD. Чему равен тангенс острого угла между диагональю АС и отрезком ВК?

Точка $K$ — середина стороны $CD$ квадрата $ABCD$;

Найти тангенс острого угла между отрезками $AC$ и $BK$;

Решение:

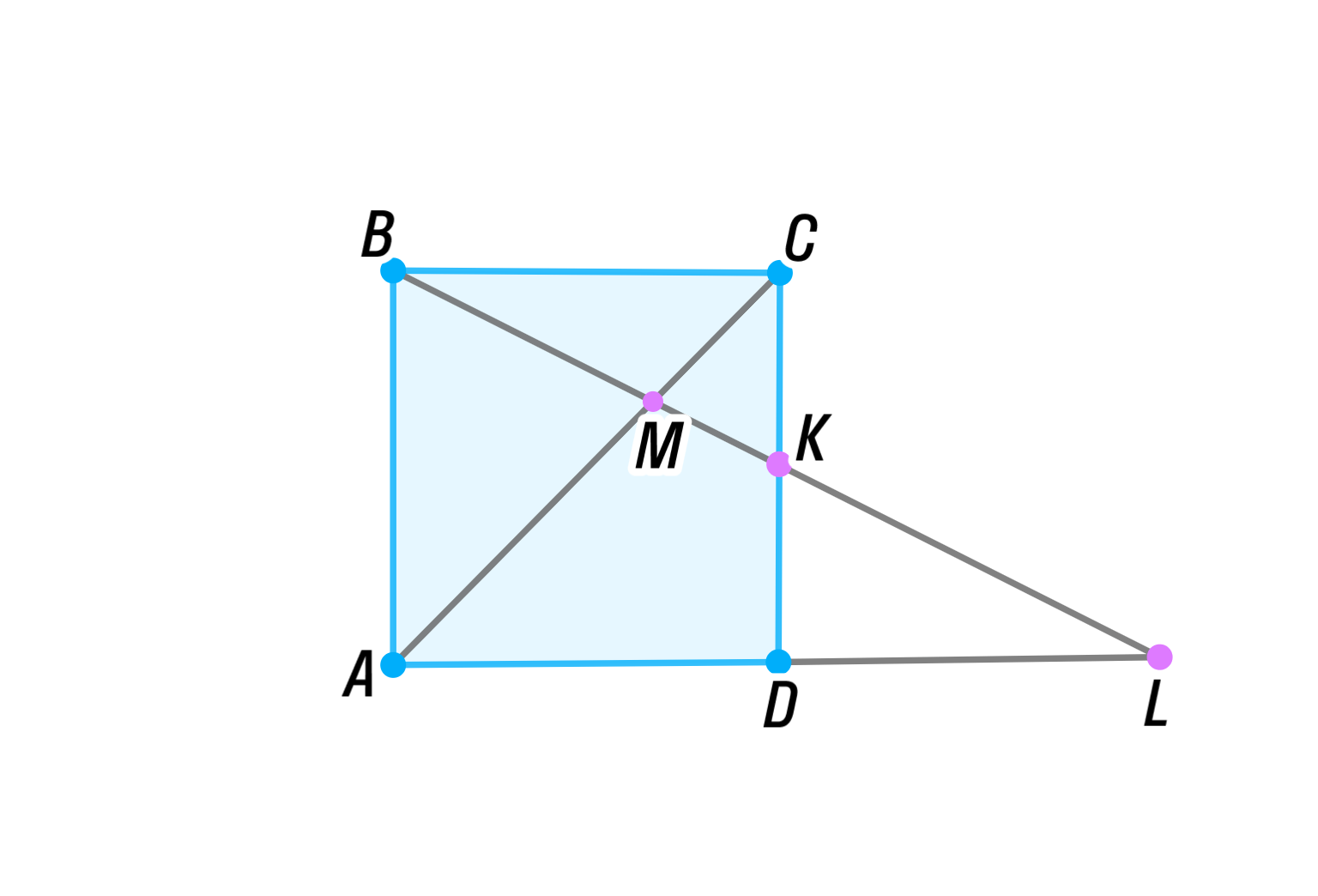
Отобразим условие задачи:

$ABCD$ — квадрат, следовательно:

$$AB = BC = CD = AD;$$ $$\angle C = \angle D = 90^\circ;$$

Рассмотрим прямоугольный треугольник $ADC$:

$$\text{tg } \angle ACD = \frac{AD}{DC} = 1;$$ $$\angle ACD = \text{arctg } 1 = \frac{\pi}{4};$$

Рассмотрим прямоугольный треугольник $BCK$:

$$CK = \frac{1}{2} CD = \frac{1}{2} BC;$$ $$\text{tg } \angle BKC = \frac{BC}{CK} = 2;$$ $$\angle BKC = \text{arctg } 2;$$

В треугольнике $CEK$, по теореме о сумме углов:

$$\angle CEK = 180^\circ — \angle ACD — \angle BKC = 180^\circ — \frac{\pi}{4} — \text{arctg } 2;$$ $$\text{tg } \angle CEK = \text{tg } \left( 180^\circ — \frac{\pi}{4} — \text{arctg } 2 \right) = -\text{tg } \left( \frac{\pi}{4} + \text{arctg } 2 \right);$$ $$\text{tg } \angle CEK = \frac{\text{tg } \frac{\pi}{4} + \text{tg } (\text{arctg } 2)}{1 — \text{tg } \frac{\pi}{4} \cdot \text{tg } (\text{arctg } 2)} = \frac{1 + 2}{1 — 1 \cdot 2} = \frac{3}{-1} = -3;$$

Ответ: $3$.

Условие:
Точка $K$ — середина стороны $CD$ квадрата $ABCD$.
Найти тангенс острого угла между отрезками $AC$ и $BK$.

Решение:

Шаг 1: Геометрия квадрата

Пусть квадрат $ABCD$ расположен на координатной плоскости следующим образом:

(Это удобно, чтобы выражать вектора и вычислять углы.)

• $A(0, 0)$
• $B(1, 0)$
• $C(1, 1)$
• $D(0, 1)$

Размер квадрата принят за 1 — можно выбрать любой размер, поскольку тангенс угла не зависит от масштаба.

Тогда:

• $AC$ — диагональ квадрата (соединяет $A$ и $C$)
• $K$ — середина стороны $CD$, т.е. середина отрезка от $C(1, 1)$ до $D(0, 1)$

Найдём координаты точки $K$:

$$K = \left( \frac{1 + 0}{2}, \frac{1 + 1}{2} \right) = \left( \frac{1}{2}, 1 \right)$$

Также у нас есть:

• $B = (1, 0)$

Шаг 2: Найдём векторы

Нас интересует угол между векторами:

• $\vec{AC} = C — A = (1, 1) — (0, 0) = (1, 1)$
• $\vec{BK} = K — B = \left( \frac{1}{2}, 1 \right) — (1, 0) = \left( -\frac{1}{2}, 1 \right)$

Шаг 3: Формула тангенса угла между векторами

Для векторов $\vec{u}$ и $\vec{v}$, угол $\theta$ между ними даёт:

$$\tan \theta = \frac{|\vec{u} \times \vec{v}|}{\vec{u} \cdot \vec{v}}$$

Вычислим скалярное произведение:

$$\vec{AC} \cdot \vec{BK} = (1)(-1/2) + (1)(1) = -\frac{1}{2} + 1 = \frac{1}{2}$$

Вычислим модуль векторного произведения (для плоскости, это псевдоскаляр):

$$|\vec{AC} \times \vec{BK}| = |(1)(1) — (1)(-1/2)| = |1 + 1/2| = \frac{3}{2}$$

Шаг 4: Тангенс угла между векторами

$$\tan \theta = \frac{\frac{3}{2}}{\frac{1}{2}} = 3$$

Ответ:

$$\boxed{3}$$

Комментарий: почему именно острый угол

Так как тангенс положительный, и скалярное произведение $\vec{AC} \cdot \vec{BK} = \frac{1}{2} > 0$, угол между векторами меньше 90°, то есть острый.