ГДЗ по Алгебре 10 Класс Номер 26.37 Профильный Уровень Мордкович — Подробные Ответы

Постройте график функции:

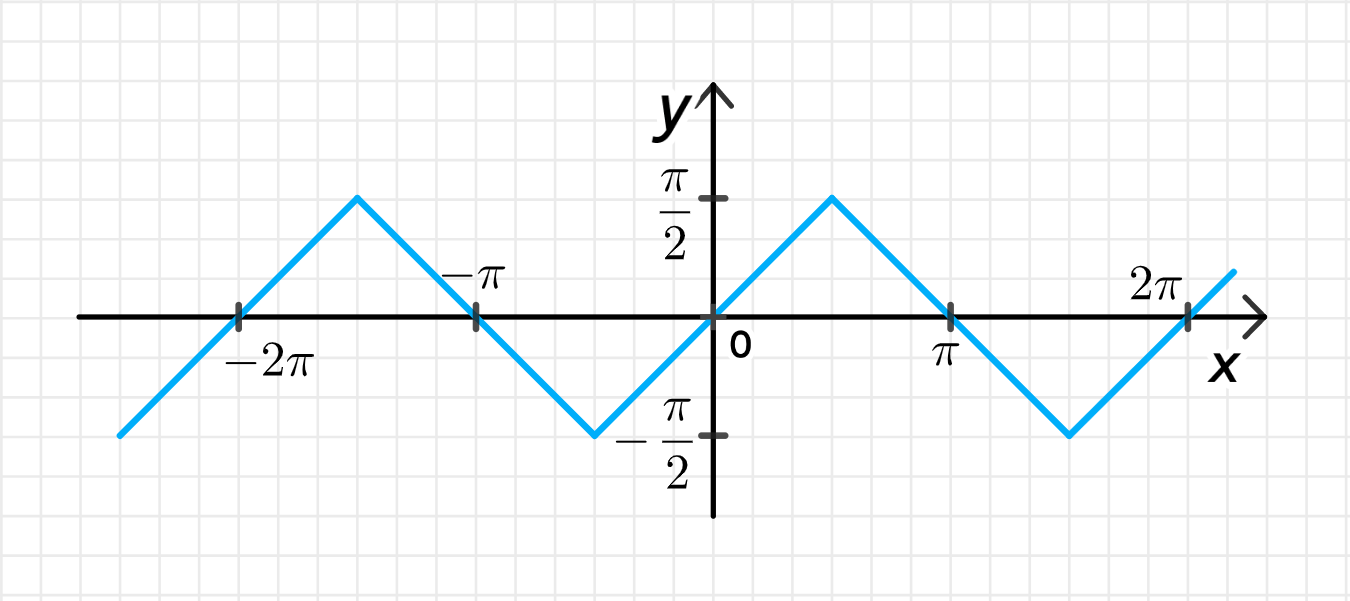
a) у = arcsin(sinх);

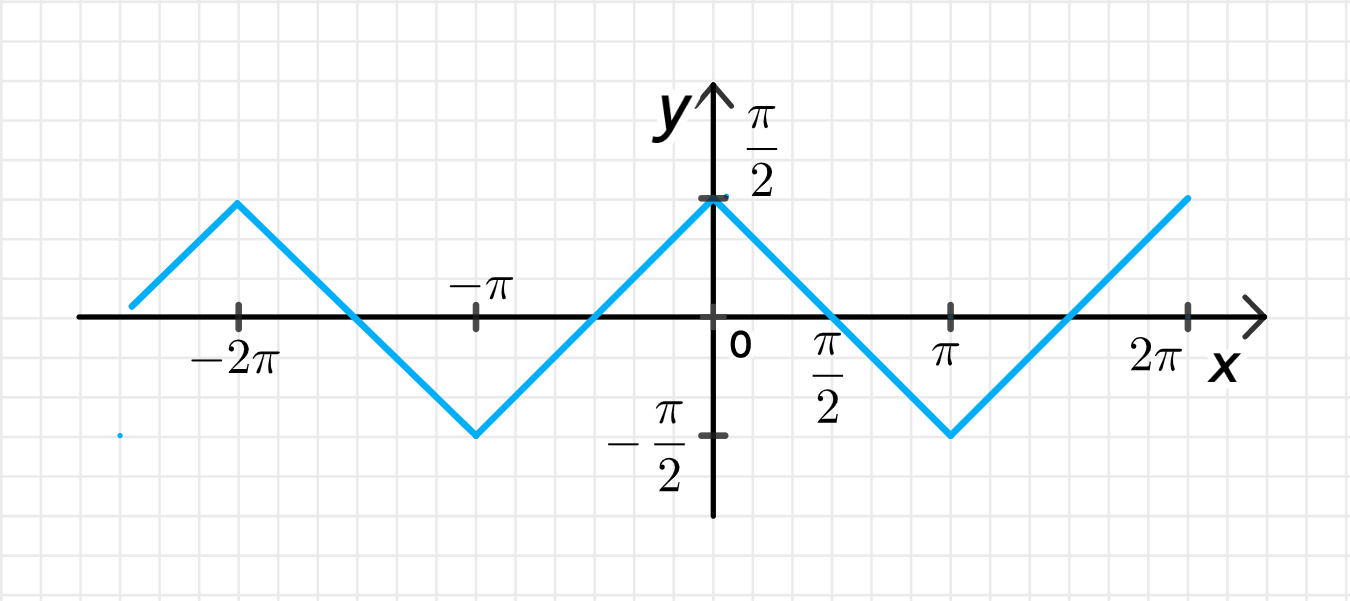
б) у = arcsin(cosх).

а) $y=\arcsin (\sin x)$;

Функция является периодической с основным периодом $T=2\pi$:

$$y(x+2\pi )=\arcsin (\sin (x+2\pi ))=\arcsin (\sin x)=y(x);$$

Функция является нечетной:

$$y(-x)=\arcsin (\sin (-x))=\arcsin (-\sin x)=-\arcsin (\sin x)=-y(x);$$

Если $0\le x\le \frac{\pi }{2}$, тогда:

$$y=\arcsin (\sin x)=x;$$$$\overline{)\begin{array}{ccc}x& 0& \frac{\pi }{2}\\ y& 0& \frac{\pi }{2}\end{array}}$$

Если $\frac{\pi }{2}\le x\le \pi$, тогда:

$$y=\arcsin (\sin x)=\arcsin (\sin (\pi -x))=\pi -x;$$$$\overline{)\begin{array}{ccc}x& \frac{\pi }{2}& \pi \\ y& \frac{\pi }{2}& 0\end{array}}$$

График функции:

б) $y=\arcsin (\cos x)$;

Функция является периодической с основным периодом $T=2\pi$:

$$y(x+2\pi )=\arcsin (\cos (x+2\pi ))=\arcsin (\cos x)=y(x);$$

Функция является четной:

$$y(-x)=\arcsin (\cos (-x))=\arcsin (\cos x)=y(x);$$

Если $0\le x\le \pi$, тогда:

$$y=\arcsin (\cos x)=\arcsin (\sin (\frac{\pi }{2}-x))=\frac{\pi }{2}-x;$$$$\overline{)\begin{array}{ccc}x& 0& \pi \\ y& \frac{\pi }{2}& -\frac{\pi }{2}\end{array}}$$

График функции:

а) $y=\arcsin (\sin x)$

1. Периодичность функции

Функция $y=\arcsin (\sin x)$ — это композиция двух функций:

• $\sin x$ — периодическая функция с периодом $2\pi$,
• $\arcsin x$ — не периодическая, но её область определения ограничена отрезком $[-1,1]$, и она берёт значения только в $[-\frac{\pi }{2},\frac{\pi }{2}]$.

Рассмотрим:

$$y(x+2\pi )=\arcsin (\sin (x+2\pi ))$$

Известно, что:

$$\sin (x+2\pi )=\sin x$$

Подставим:

$$y(x+2\pi )=\arcsin (\sin x)=y(x)$$

Вывод:
Функция $y=\arcsin (\sin x)$ является периодической с периодом $T=2\pi$.

2. Чётность / Нечётность функции

Проверим, является ли функция чётной или нечётной. Для этого исследуем значение при $-x$:

$$y(-x)=\arcsin (\sin (-x))$$

Поскольку $\sin (-x)=-\sin x$, то:

$$y(-x)=\arcsin (-\sin x)$$

Функция $\arcsin x$ нечётная, т.е. $\arcsin (-x)=-\arcsin (x)$, поэтому:

$$y(-x)=-\arcsin (\sin x)=-y(x)$$

Вывод:
Функция $y=\arcsin (\sin x)$ нечётная.

3. Поведение на отрезке $0\le x\le \frac{\pi }{2}$

На этом отрезке:

• $x\in [0,\frac{\pi }{2}]$,
• $\sin x\in [0,1]$,
• $\arcsin (\sin x)\in [0,\frac{\pi }{2}]$,
• $\arcsin (\sin x)=x$, так как $x$ уже лежит в области значений $\arcsin$, где он совпадает с $x$.

Прямое вычисление:

$$y=\arcsin (\sin x)=x$$

Таблица:

$$\overline{)\begin{array}{ccc}x& 0& \frac{\pi }{2}\\ y=\arcsin (\sin x)& 0& \frac{\pi }{2}\end{array}}$$

4. Поведение на отрезке $\frac{\pi }{2}\le x\le \pi$

В этом интервале:

• $\sin x\in [0,1]$, поскольку $\sin x$ убывает от $1$ до $0$,
• Однако $x\mathrm{\notin }[-\frac{\pi }{2},\frac{\pi }{2}]$, то есть нельзя напрямую сказать, что $\arcsin (\sin x)=x$,
• Используем тригонометрическую идентичность:$$\sin x=\sin (\pi -x)$$

  Тогда:

  $$y=\arcsin (\sin x)=\arcsin (\sin (\pi -x))=\pi -x$$

Проверим это на краях:

• При $x=\frac{\pi }{2}$: $y=\pi -\frac{\pi }{2}=\frac{\pi }{2}$
• При $x=\pi$: $y=\pi -\pi =0$

Таблица:

$$\overline{)\begin{array}{ccc}x& \frac{\pi }{2}& \pi \\ y=\arcsin (\sin x)& \frac{\pi }{2}& 0\end{array}}$$

5. График функции

График функции $y=\arcsin (\sin x)$:

• Имеет вид пилообразной (зубчатой) линии, так как:
  • От $x=-\frac{\pi }{2}$ до $x=\frac{\pi }{2}$ — это просто линия $y=x$,
  • От $\frac{\pi }{2}$ до $\pi$ — линия убывает: $y=\pi -x$,
  • Потом повторяется с периодом $2\pi$,
  • Симметрия относительно начала координат (нечётная).

б) $y=\arcsin (\cos x)$

1. Периодичность

Функция $\cos x$ — периодическая с периодом $2\pi$, а значит:

$$y(x+2\pi )=\arcsin (\cos (x+2\pi ))=\arcsin (\cos x)=y(x)$$

Вывод:
Функция периодическая, с периодом $T=2\pi$.

2. Чётность функции

Проверим значение при $-x$:

$$y(-x)=\arcsin (\cos (-x))=\arcsin (\cos x)$$

Так как $\cos (-x)=\cos x$, то:

$$y(-x)=y(x)$$

Вывод:
Функция чётная.

3. Поведение на отрезке $0\le x\le \pi$

На этом интервале:

• $\cos x\in [-1,1]$,
• Заметим:$$\cos x=\sin (\frac{\pi }{2}-x)$$

  Поэтому:

  $$y=\arcsin (\cos x)=\arcsin (\sin (\frac{\pi }{2}-x))$$

Если $\frac{\pi }{2}-x\in [-\frac{\pi }{2},\frac{\pi }{2}]$, то:

$$\arcsin (\sin (\frac{\pi }{2}-x))=\frac{\pi }{2}-x$$

Так как $0\le x\le \pi$, то $\frac{\pi }{2}-x\in [-\frac{\pi }{2},\frac{\pi }{2}]$, всё корректно.

Итак:

$$y=\frac{\pi }{2}-x$$

Таблица:

$$\overline{)\begin{array}{ccc}x& 0& \pi \\ y=\arcsin (\cos x)& \frac{\pi }{2}& -\frac{\pi }{2}\end{array}}$$

4. График функции

Функция $y=\arcsin (\cos x)$:

• Определена на всей числовой прямой,
• Чётная,
• Периодическая с периодом $2\pi$,
• На интервале $[0,\pi ]$: прямая убывающая линия $y=\frac{\pi }{2}-x$,
• Потом повторяется,
• Значения функции: $y\in [-\frac{\pi }{2},\frac{\pi }{2}]$, так как это область значений арксинуса.