ГДЗ по Алгебре 10 Класс Номер 27.68 Профильный Уровень Мордкович — Подробные Ответы

Постройте график функции:

а) $y=4\sin \frac{x}{4}\cdot \cos \frac{x}{4}$

б) $y=2{\cos }^{2}x$

а) $y = 4 \sin \frac{x}{4} \cdot \cos \frac{x}{4} = 2 \sin \frac{2x}{4} = 2 \sin \frac{x}{2}$;

Построим одну дугу графика функции $y = \sin x$, а затем:

• Совершим ее растяжение от оси $Oy$ с коэффициентом $k = 2$;
• Совершим ее растяжение от оси $Ox$ с коэффициентом $k = 2$;

Достроим график функции:

б) $y = 2 \cos^2 x = 2 \cdot \frac{1 + \cos 2x}{2} = 1 + \cos 2x$;

Построим одну дугу графика функции $y = \cos x$, а затем:

• Совершим ее сжатие к оси $Oy$ с коэффициентом $k = 2$;
• Переместим ее на 1 единицу вверх вдоль оси ординат;

Достроим график функции:

а) $y = 4 \sin \frac{x}{4} \cdot \cos \frac{x}{4} = 2 \sin \frac{2x}{4} = 2 \sin \frac{x}{2}$

Приводим к более простому виду:

Сначала рассмотрим выражение:

$$y = 4 \sin \frac{x}{4} \cdot \cos \frac{x}{4}$$

Используя формулу произведения синуса и косинуса:

$$2 \sin A \cos A = \sin(2A)$$

Подставляем $A = \frac{x}{4}$, получаем:

$$y = 2 \sin \frac{x}{2}$$

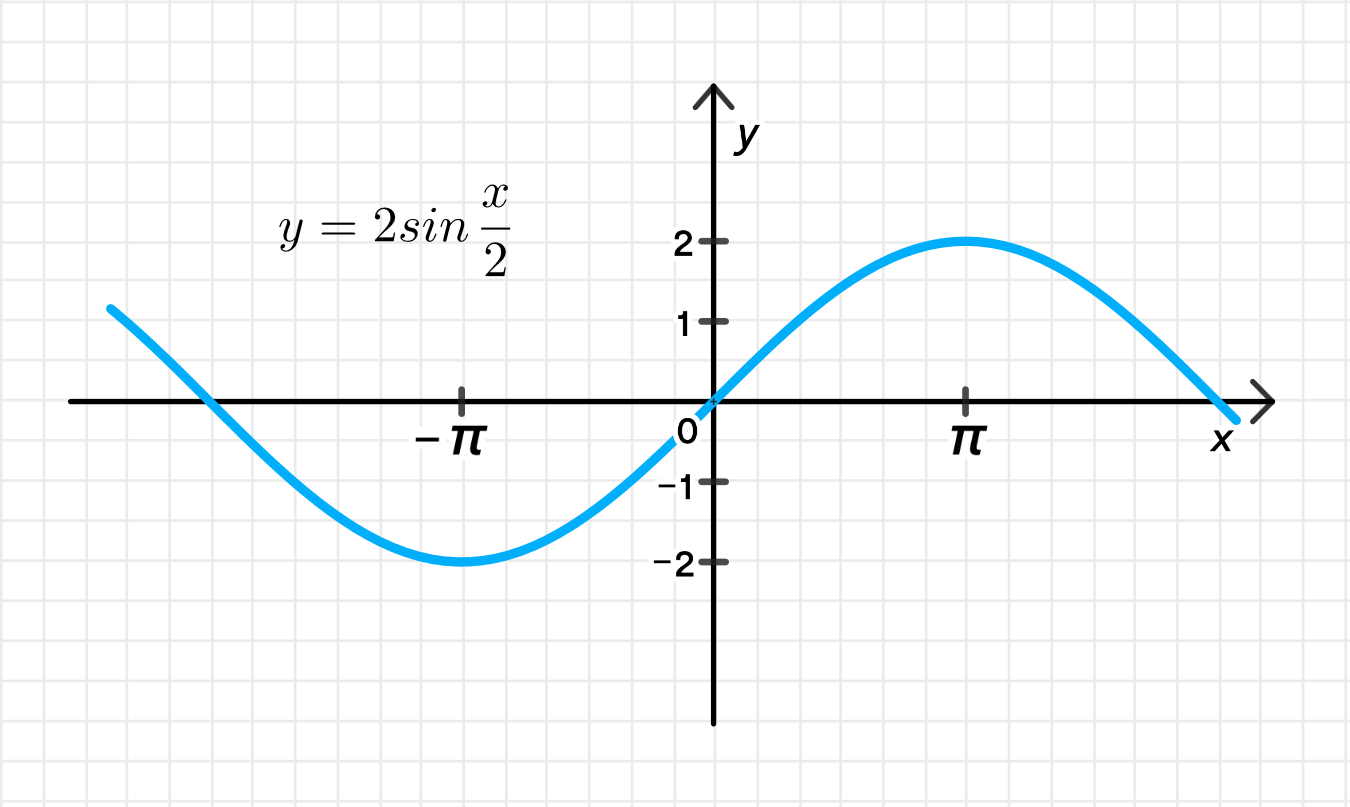
Таким образом, функция $y$ превращается в $y = 2 \sin \frac{x}{2}$.

График функции:

Теперь нам нужно построить график функции $y = 2 \sin \frac{x}{2}$. Для этого, сначала построим график функции $y = \sin x$, а затем применим два изменения, описанных в задаче:

• Растяжение от оси $Oy$ с коэффициентом $k = 2$:
  • Когда коэффициент перед синусом увеличивается, то график растягивается по вертикали (ось $Oy$). В данном случае, коэффициент $2$ означает, что амплитуда функции увеличится в 2 раза.
• Растяжение от оси $Ox$ с коэффициентом $k = 2$:
  • При увеличении коэффициента в аргументе синуса, график сжимается по оси $x$. В данном случае коэффициент $\frac{x}{2}$ означает, что период функции увеличивается в 2 раза (график растягивается по оси $x$).

Достроим график функции:

После применения растяжения, мы получаем график функции $y = 2 \sin \frac{x}{2}$, который будет иметь амплитуду 2 и период, удлиненный в два раза по сравнению с исходной функцией $y = \sin x$.

График функции выглядит следующим образом:

б) $y = 2 \cos^2 x = 2 \cdot \frac{1 + \cos 2x}{2} = 1 + \cos 2x$

Приводим к более простому виду:

Начнем с выражения:

$$y = 2 \cos^2 x$$

Используем тождество для косинуса квадрата:

$$\cos^2 x = \frac{1 + \cos 2x}{2}$$

Подставляем в исходное выражение:

$$y = 2 \cdot \frac{1 + \cos 2x}{2} = 1 + \cos 2x$$

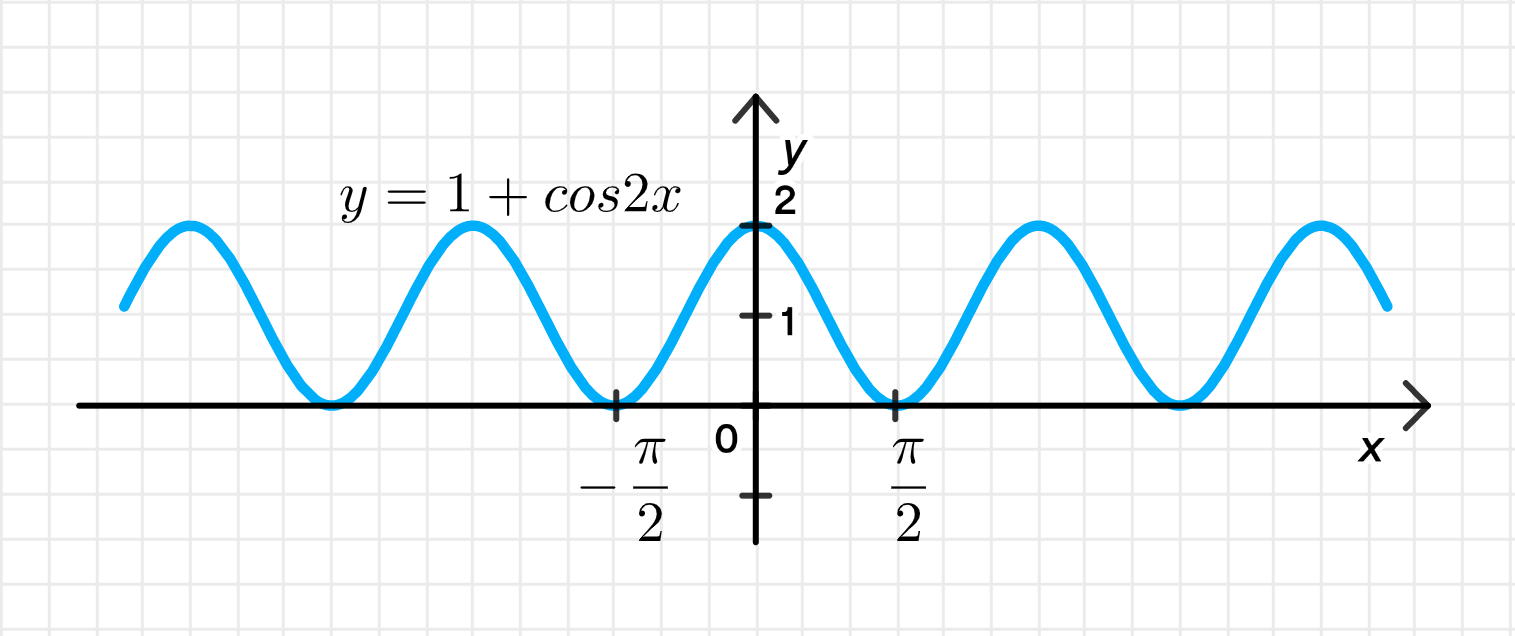
Таким образом, функция $y$ упрощается до:

$$y = 1 + \cos 2x$$

График функции:

Теперь нам нужно построить график функции $y = 1 + \cos 2x$. Для этого мы рассмотрим базовую функцию $y = \cos x$ и применим следующие изменения:

• Сжатие по оси $Oy$ с коэффициентом $k = 2$:
  • Сначала, если перед косинусом стоит коэффициент, это влияет на амплитуду функции. Однако, в нашем случае коэффициент перед косинусом равен 1, поэтому амплитуда остаётся той же.
• Перемещение на 1 единицу вверх вдоль оси ординат:
  • При добавлении константы 1 к функции $\cos 2x$, график сдвигается на 1 единицу вверх по оси $y$. Это означает, что вся волна будет двигаться вверх, и её минимум будет равен 0, а максимум 2.

Достроим график функции:

После применения сжатия и сдвига, мы получаем график функции $y = 1 + \cos 2x$, где:

• Амплитуда функции остаётся 1.
• Период функции будет в два раза меньше по сравнению с функцией $y = \cos x$, так как у нас есть коэффициент 2 перед $x$, что сжимает график по оси $x$ в два раза.
• График будет сдвинут вверх на 1 единицу.

График функции выглядит следующим образом: