ГДЗ по Алгебре 10 Класс Номер 27.69 Профильный Уровень Мордкович — Подробные Ответы

Постройте график функции:

а) $y=\sqrt{\frac{1+\cos x}{1-\cos x}}$

б) $y=-\sqrt{\frac{1-\cos 2x}{1+\cos 2x}}$

а) $y = \sqrt{\frac{1 + \cos x}{1 — \cos x}} = \sqrt{\frac{1}{\operatorname{tg}^2 \frac{x}{2}}} = \sqrt{\operatorname{ctg}^2 \frac{x}{2}} = \left| \operatorname{ctg} \frac{x}{2} \right|;$

Если $\operatorname{ctg} \frac{x}{2} \geq 0$, тогда:

$$y = \left| \operatorname{ctg} \frac{x}{2} \right| = \operatorname{ctg} \frac{x}{2};$$

Если $\operatorname{ctg} \frac{x}{2} < 0$, тогда:

$$y = \left| \operatorname{ctg} \frac{x}{2} \right| = -\operatorname{ctg} \frac{x}{2};$$

График функции:

б) $y = -\sqrt{\frac{1 — \cos 2x}{1 + \cos 2x}} = -\sqrt{\operatorname{tg}^2 x} = -|\operatorname{tg} x|;$

Если $\operatorname{tg} x \geq 0$, тогда:

$$y = -|\operatorname{tg} x| = -\operatorname{tg} x;$$

Если $\operatorname{tg} x < 0$, тогда:

$$y = -|\operatorname{tg} x| = \operatorname{tg} x;$$

График функции:

а) $y = \sqrt{\frac{1 + \cos x}{1 — \cos x}} = \sqrt{\frac{1}{\operatorname{tg}^2 \frac{x}{2}}} = \sqrt{\operatorname{ctg}^2 \frac{x}{2}} = \left| \operatorname{ctg} \frac{x}{2} \right|$

Преобразуем выражение:

Данное выражение можно упростить, используя тождества для тригонометрических функций. Сначала выразим $\cos x$ через тангенс половинного угла. Мы знаем, что:

$$\cos x = 1 — 2 \sin^2 \frac{x}{2}$$

Однако, для упрощения, лучше воспользоваться известной формулой, которая выражает дробь через тангенс:

$$\frac{1 + \cos x}{1 — \cos x} = \frac{1 + \cos x}{\sin^2 x} = \frac{1}{\operatorname{tg}^2 \frac{x}{2}}$$

Подставим это в исходное выражение:

$$y = \sqrt{\frac{1}{\operatorname{tg}^2 \frac{x}{2}}}$$

Это упрощается до:

$$y = \frac{1}{\left|\operatorname{tg} \frac{x}{2}\right|}$$

Но, так как $\operatorname{tg} \frac{x}{2} = \frac{1}{\operatorname{ctg} \frac{x}{2}}$, получаем:

$$y = \left|\operatorname{ctg} \frac{x}{2}\right|$$

Рассматриваем два случая для абсолютного значения:

Теперь рассмотрим два случая для абсолютного значения $\left|\operatorname{ctg} \frac{x}{2}\right|$.

• Если $\operatorname{ctg} \frac{x}{2} \geq 0$, то:
  В этом случае $\left|\operatorname{ctg} \frac{x}{2}\right| = \operatorname{ctg} \frac{x}{2}$, и следовательно, функция будет равна:

  $$y = \operatorname{ctg} \frac{x}{2}$$

• Если $\operatorname{ctg} \frac{x}{2} < 0$, то:
  В этом случае $\left|\operatorname{ctg} \frac{x}{2}\right| = -\operatorname{ctg} \frac{x}{2}$, и следовательно, функция будет равна:

  $$y = -\operatorname{ctg} \frac{x}{2}$$

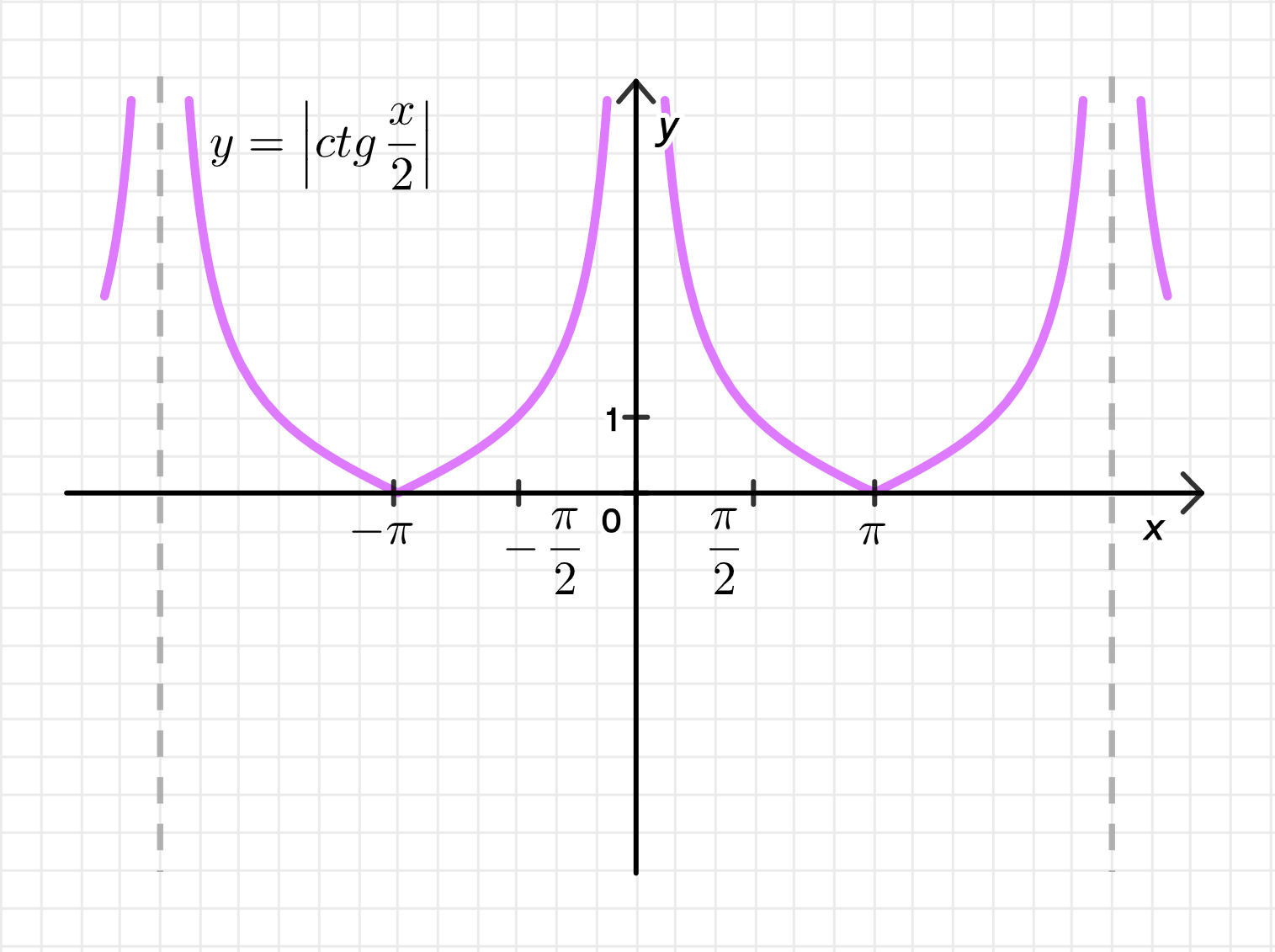
График функции:

График функции $y = \left| \operatorname{ctg} \frac{x}{2} \right|$ будет отображать абсолютное значение котангенса половинного угла. Это означает, что график функции будет симметричен относительно оси $x$, и все отрицательные значения будут преобразованы в положительные.

б) $y = -\sqrt{\frac{1 — \cos 2x}{1 + \cos 2x}} = -\sqrt{\operatorname{tg}^2 x} = -|\operatorname{tg} x|$

Преобразуем выражение:

Подобным образом, начнем с упрощения выражения $y = -\sqrt{\frac{1 — \cos 2x}{1 + \cos 2x}}$. Мы используем известное тригонометрическое тождество для выражения косинуса двойного угла:

$$\cos 2x = 1 — 2 \sin^2 x$$

Однако, проще использовать формулу для тангенса половинного угла:

$$\frac{1 — \cos 2x}{1 + \cos 2x} = \operatorname{tg}^2 x$$

Следовательно, выражение для $y$ становится:

$$y = -\sqrt{\operatorname{tg}^2 x}$$

Это упрощается до:

$$y = -|\operatorname{tg} x|$$

Рассматриваем два случая для абсолютного значения:

Аналогично предыдущему случаю, мы имеем два случая:

• Если $\operatorname{tg} x \geq 0$, то:
  В этом случае $|\operatorname{tg} x| = \operatorname{tg} x$, и следовательно:

  $$y = -\operatorname{tg} x$$

• Если $\operatorname{tg} x < 0$, то:
  В этом случае $|\operatorname{tg} x| = -\operatorname{tg} x$, и следовательно:

  $$y = \operatorname{tg} x$$

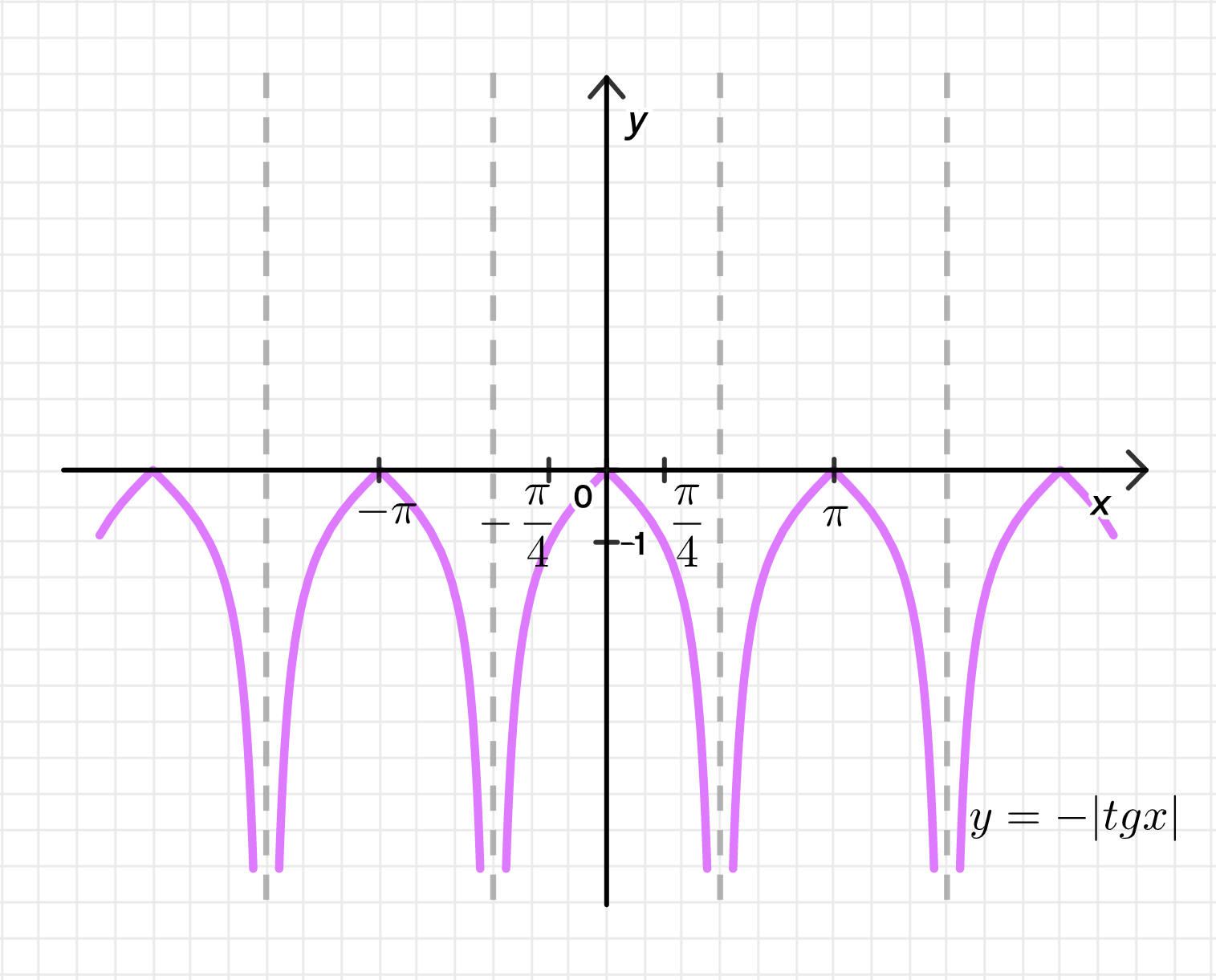
График функции:

График функции $y = -|\operatorname{tg} x|$ будет отображать абсолютно значение тангенса, но с отрицательным знаком для положительных значений тангенса и с положительным знаком для отрицательных значений. Это означает, что график будет зеркально отражен по отношению к графику функции $y = \operatorname{tg} x$, с дополнительным сжатием (так как используется абсолютное значение).