ГДЗ по Алгебре 10 Класс Номер 27.71 Профильный Уровень Мордкович — Подробные Ответы

Постройте график функции:

а) $y=\frac{\cos 2x}{\sin x-\cos x}+\sin x$

б) $y=\frac{\cos 2x}{\cos x+\sin x}-\cos x$

в) $y=\frac{\cos 2x}{\cos x+\sin x}+\sin x$

г) $y=\frac{\cos 2x}{\cos x-\sin x}-\cos x$

а)

$$y=\frac{\cos 2x}{\sin x-\cos x}+\sin x;$$

$$$$$$y=\frac{{\cos }^{2}x-{\sin }^{2}x}{\sin x-\cos x}+\sin x;$$

$$$$$$y=\frac{(\cos x-\sin x)(\cos x+\sin x)}{-(\cos x-\sin x)}+\sin x;$$

$$$$$$y=-(\cos x+\sin x)+\sin x=-\cos x;$$

1) Выражение имеет смысл при:

$$\sin x-\cos x\mathrm{\ne }0\mathrm{\mid }:\cos x;$$

$$$$$$\mathrm{tg}x-1\mathrm{\ne }0;$$

$$$$$$\mathrm{tg}x\mathrm{\ne }1;$$

$$$$$$x\mathrm{\ne }\mathrm{arctg}1+\pi n=\frac{\pi }{4}+\pi n;$$

2) График функции:

б)

$$y=\frac{\cos 2x}{\cos x+\sin x}-\cos x;$$

$$$$$$y=\frac{{\cos }^{2}x-{\sin }^{2}x}{\cos x+\sin x}-\cos x;$$

$$$$$$y=\frac{(\cos x-\sin x)(\cos x+\sin x)}{\cos x+\sin x}-\cos x;$$

$$$$$$y=(\cos x-\sin x)-\cos x=-\sin x;$$

1) Выражение имеет смысл при:

$$\cos x+\sin x\mathrm{\ne }0\mathrm{\mid }:\cos x;$$

$$$$$$1+\mathrm{tg}x\mathrm{\ne }0;$$

$$$$$$\mathrm{tg}x\mathrm{\ne }-1;$$

$$$$$$x\mathrm{\ne }-\mathrm{arctg}1+\pi n=-\frac{\pi }{4}+\pi n;$$

2) График функции:

в)

$$y=\frac{\cos 2x}{\cos x+\sin x}+\sin x;$$

$$$$$$y=\frac{{\cos }^{2}x-{\sin }^{2}x}{\cos x+\sin x}+\sin x;$$

$$$$$$y=\frac{(\cos x-\sin x)(\cos x+\sin x)}{\cos x+\sin x}+\sin x;$$

$$$$$$y=(\cos x-\sin x)+\sin x=\cos x;$$

1) Выражение имеет смысл при:

$$\cos x+\sin x\mathrm{\ne }0\mathrm{\mid }:\cos x;$$

$$$$$$1+\mathrm{tg}x\mathrm{\ne }0;$$

$$$$$$\mathrm{tg}x\mathrm{\ne }-1;$$

$$$$$$x\mathrm{\ne }\mathrm{arctg}1+\pi n=-\frac{\pi }{4}+\pi n;$$

2) График функции:

г)

$$y=\frac{\cos 2x}{\cos x-\sin x}-\cos x;$$

$$$$$$y=\frac{{\cos }^{2}x-{\sin }^{2}x}{\cos x-\sin x}-\cos x;$$

$$$$$$y=\frac{(\cos x-\sin x)(\cos x+\sin x)}{\cos x-\sin x}-\cos x;$$

$$$$$$y=(\cos x+\sin x)-\cos x=\sin x;$$

1) Выражение имеет смысл при:

$$\cos x-\sin x\mathrm{\ne }0\mathrm{\mid }:\cos x;$$

$$$$$$1-\mathrm{tg}x\mathrm{\ne }0;$$

$$$$$$\mathrm{tg}x\mathrm{\ne }1;$$

$$$$$$x\mathrm{\ne }\mathrm{arctg}1+\pi n=\frac{\pi }{4}+\pi n;$$

2) График функции:

а) $y=\frac{\cos 2x}{\sin x-\cos x}+\sin x$

Преобразование выражения:

Рассмотрим исходную функцию:

$$y=\frac{\cos 2x}{\sin x-\cos x}+\sin x$$

Используем формулу для косинуса двойного угла:

$$\cos 2x={\cos }^{2}x-{\sin }^{2}x$$

Подставляем это в выражение для $y$:

$$y=\frac{{\cos }^{2}x-{\sin }^{2}x}{\sin x-\cos x}+\sin x$$

Теперь преобразуем дробь. Разложим числитель:

$$y=\frac{(\cos x-\sin x)(\cos x+\sin x)}{\sin x-\cos x}+\sin x$$

Заметим, что $\sin x-\cos x=-(\cos x-\sin x)$. Подставим это:

$$y=\frac{(\cos x-\sin x)(\cos x+\sin x)}{-(\cos x-\sin x)}+\sin x$$

Сокращаем $\cos x-\sin x$ в числителе и знаменателе:

$$y=-(\cos x+\sin x)+\sin x$$

Упрощаем:

$$y=-\cos x$$

Таким образом, получаем выражение:

$$y=-\cos x$$

Условия, при которых выражение имеет смысл:

Рассмотрим выражение $y=\frac{\cos 2x}{\sin x-\cos x}$. Оно имеет смысл только тогда, когда знаменатель не равен нулю, то есть $\sin x-\cos x\mathrm{\ne }0$.

Заменим выражение $\sin x-\cos x=0$, когда $x=\frac{\pi }{4}+\pi n$, где $n$ — целое число. Следовательно, выражение имеет смысл при:

$$\sin x-\cos x\mathrm{\ne }0\Rightarrow x\mathrm{\ne }\frac{\pi }{4}+\pi n$$

Также это можно записать как:

$$\mathrm{tg}x-1\mathrm{\ne }0\Rightarrow \mathrm{tg}x\mathrm{\ne }1$$

Таким образом, $x\mathrm{\ne }\mathrm{arctg}1+\pi n=\frac{\pi }{4}+\pi n$.

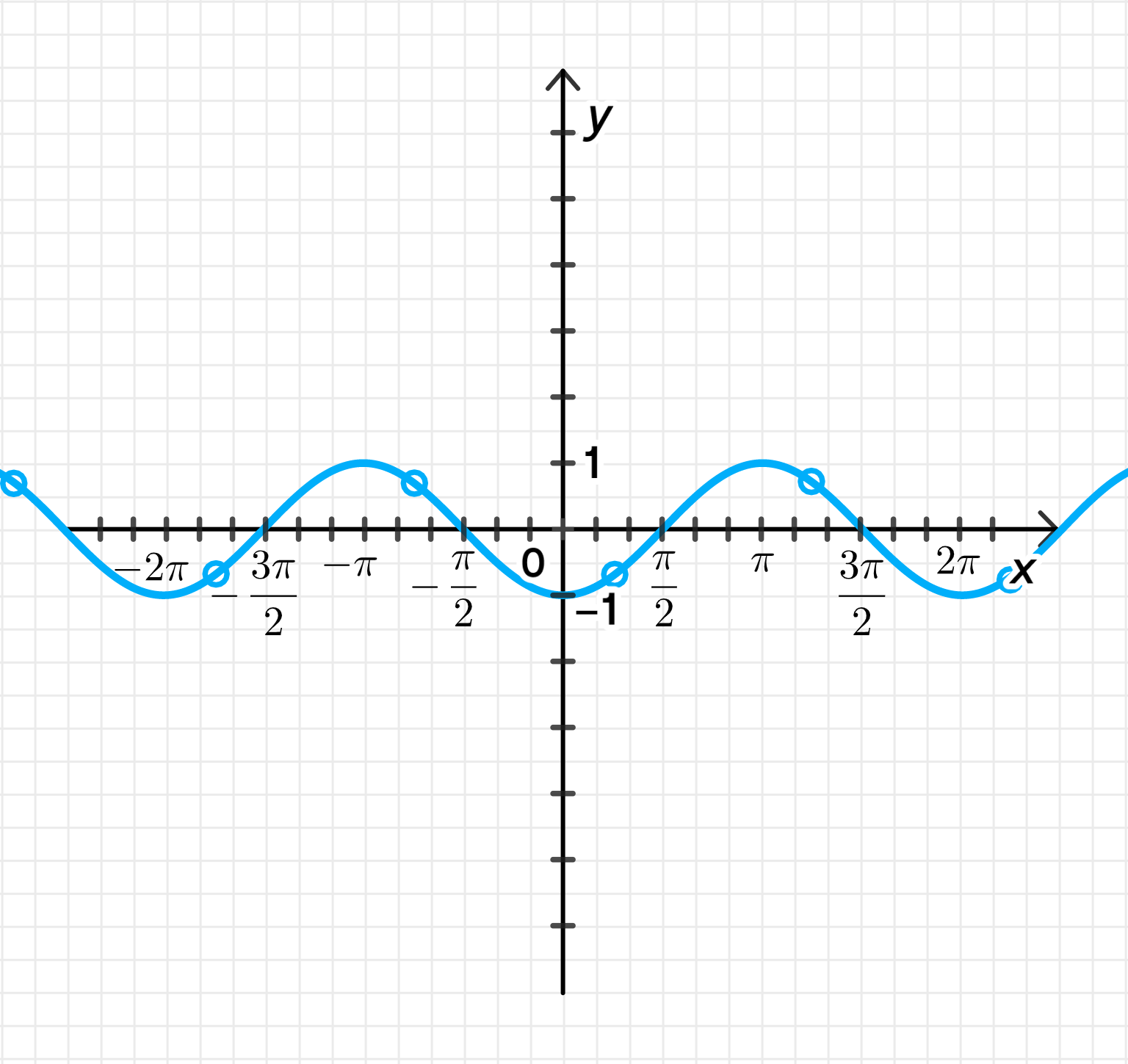
График функции:

График функции $y=-\cos x$ будет зеркальным отображением графика функции $y=\cos x$ относительно оси $x$. Период функции $y=\cos x$ равен $2\pi$, и аналогично для функции $y=-\cos x$ период также будет равен $2\pi$. Амплитуда будет равна 1, но фаза функции будет изменена. График будет начинаться с минимального значения $-1$, а максимальное значение будет равно 1.

б) $y=\frac{\cos 2x}{\cos x+\sin x}-\cos x$

Преобразование выражения:

Рассмотрим выражение:

$$y=\frac{\cos 2x}{\cos x+\sin x}-\cos x$$

Используем формулу для косинуса двойного угла:

$$\cos 2x={\cos }^{2}x-{\sin }^{2}x$$

Подставляем это в выражение для $y$:

$$y=\frac{{\cos }^{2}x-{\sin }^{2}x}{\cos x+\sin x}-\cos x$$

Теперь у нас выражение:

$$y=\frac{(\cos x-\sin x)(\cos x+\sin x)}{\cos x+\sin x}-\cos x$$

Сокращаем $\cos x+\sin x$ в числителе и знаменателе:

$$y=(\cos x-\sin x)-\cos x$$

Упрощаем:

$$y=-\sin x$$

Таким образом, получаем выражение:

$$y=-\sin x$$

Условия, при которых выражение имеет смысл:

Чтобы выражение $y=\frac{\cos 2x}{\cos x+\sin x}$ имело смысл, знаменатель не должен равняться нулю, то есть $\cos x+\sin x\mathrm{\ne }0$.

Заменим выражение $\cos x+\sin x=0$, когда $x=-\frac{\pi }{4}+\pi n$, где $n$ — целое число. Следовательно, выражение имеет смысл при:

$$\cos x+\sin x\mathrm{\ne }0\Rightarrow x\mathrm{\ne }-\frac{\pi }{4}+\pi n$$

Это условие также можно записать как:

$$1+\mathrm{tg}x\mathrm{\ne }0\Rightarrow \mathrm{tg}x\mathrm{\ne }-1$$

Таким образом, $x\mathrm{\ne }-\mathrm{arctg}1+\pi n=-\frac{\pi }{4}+\pi n$.

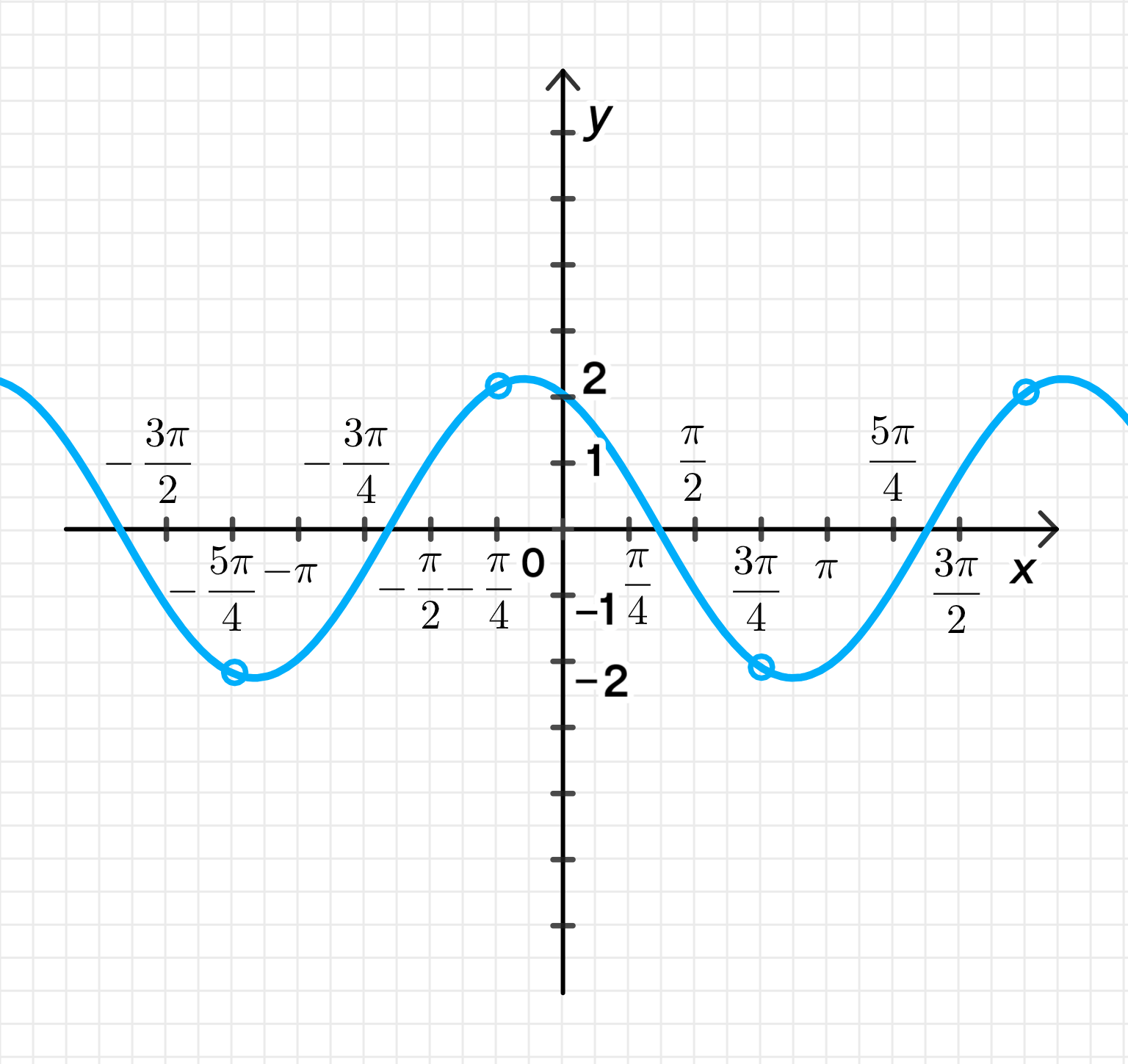
График функции:

График функции $y=-\sin x$ будет аналогичен графику функции $y=\sin x$, но с перевернутой фазой. Период функции $y=\sin x$ равен $2\pi$, и для функции $y=-\sin x$ период останется таким же. Амплитуда будет равна 1, и график будет начинаться с минимального значения $-1$, а максимальное значение будет равно 1.

в) $y=\frac{\cos 2x}{\cos x+\sin x}+\sin x$

Преобразование выражения:

Рассмотрим выражение:

$$y=\frac{\cos 2x}{\cos x+\sin x}+\sin x$$

Используем формулу для косинуса двойного угла:

$$\cos 2x={\cos }^{2}x-{\sin }^{2}x$$

Подставляем это в выражение для $y$:

$$y=\frac{{\cos }^{2}x-{\sin }^{2}x}{\cos x+\sin x}+\sin x$$

Теперь у нас выражение:

$$y=\frac{(\cos x-\sin x)(\cos x+\sin x)}{\cos x+\sin x}+\sin x$$

Сокращаем $\cos x+\sin x$ в числителе и знаменателе:

$$y=(\cos x-\sin x)+\sin x$$

Упрощаем:

$$y=\cos x$$

Таким образом, получаем выражение:

$$y=\cos x$$

Условия, при которых выражение имеет смысл:

Чтобы выражение $y=\frac{\cos 2x}{\cos x+\sin x}$ имело смысл, знаменатель не должен равняться нулю, то есть $\cos x+\sin x\mathrm{\ne }0$.

Заменим выражение $\cos x+\sin x=0$, когда $x=-\frac{\pi }{4}+\pi n$, где $n$ — целое число. Следовательно, выражение имеет смысл при:

$$\cos x+\sin x\mathrm{\ne }0\Rightarrow x\mathrm{\ne }-\frac{\pi }{4}+\pi n$$

Это условие также можно записать как:

$$1+\mathrm{tg}x\mathrm{\ne }0\Rightarrow \mathrm{tg}x\mathrm{\ne }-1$$

Таким образом, $x\mathrm{\ne }\mathrm{arctg}1+\pi n=-\frac{\pi }{4}+\pi n$.

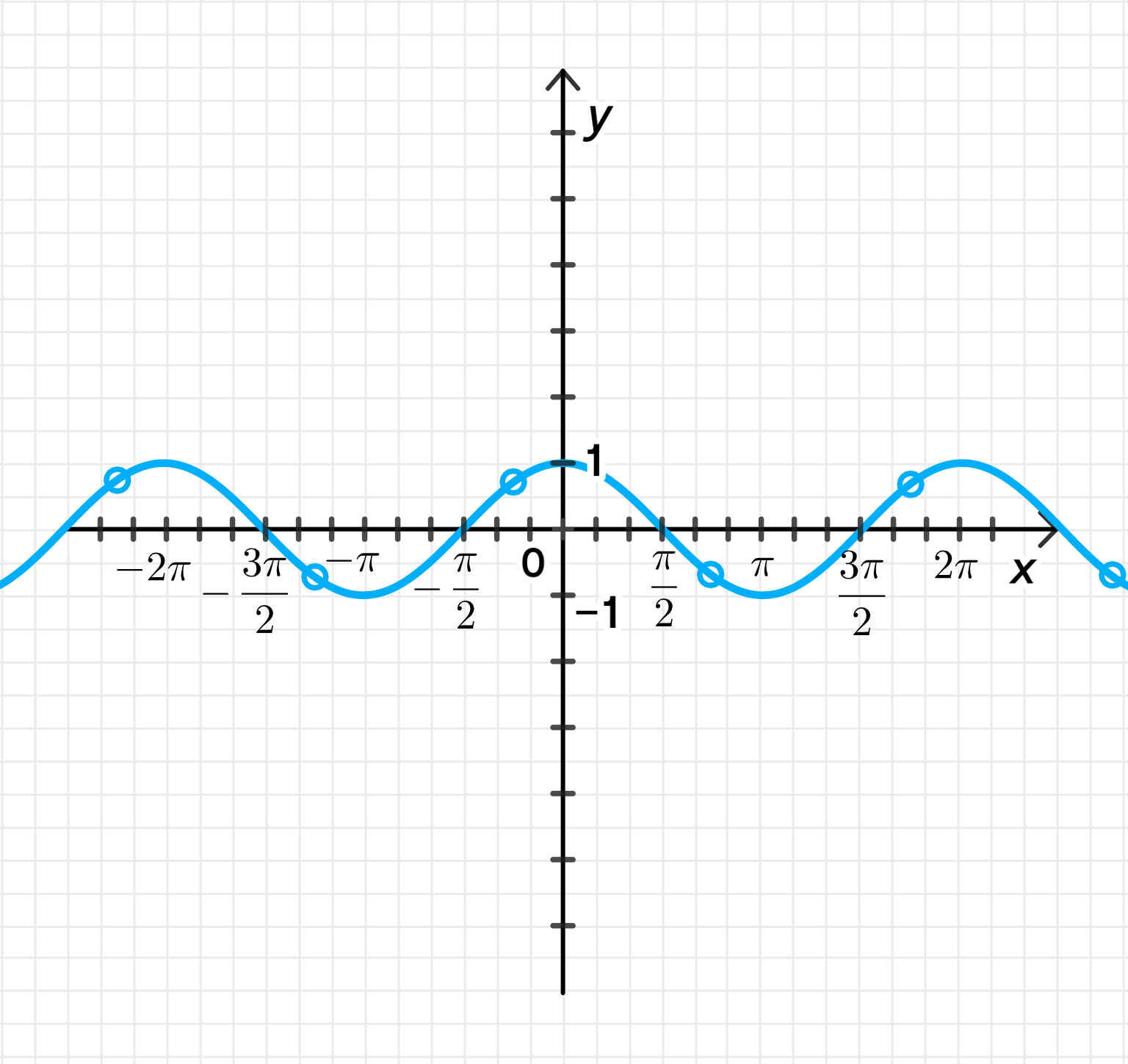
График функции:

График функции $y=\cos x$ будет представлять собой стандартную синусоиду с амплитудой 1 и периодом $2\pi$. Он будет колебаться между значениями $-1$ и $1$, начиная с максимума $1$ при $x=0$, с минимальным значением $-1$ в $\pi$, и снова возвращаться к максимуму при $2\pi$.

г) $y=\frac{\cos 2x}{\cos x-\sin x}-\cos x$

Преобразование выражения:

Рассмотрим выражение:

$$y=\frac{\cos 2x}{\cos x-\sin x}-\cos x$$

Используем формулу для косинуса двойного угла:

$$\cos 2x={\cos }^{2}x-{\sin }^{2}x$$

Подставляем это в выражение для $y$:

$$y=\frac{{\cos }^{2}x-{\sin }^{2}x}{\cos x-\sin x}-\cos x$$

Теперь у нас выражение:

$$y=\frac{(\cos x-\sin x)(\cos x+\sin x)}{\cos x-\sin x}-\cos x$$

Сокращаем $\cos x-\sin x$ в числителе и знаменателе:

$$y=(\cos x+\sin x)-\cos x$$

Упрощаем:

$$y=\sin x$$

Таким образом, получаем, что:

$$y=\sin x$$

Условия, при которых выражение имеет смысл:

Чтобы выражение $y=\frac{\cos 2x}{\cos x-\sin x}$ имело смысл, знаменатель не должен равняться нулю, то есть:

$$\cos x-\sin x\mathrm{\ne }0$$

Это выражение равно нулю, когда $\cos x=\sin x$, что происходит при $x=\frac{\pi }{4}+\pi n$, где $n$ — целое число. Следовательно, выражение имеет смысл при:

$$\cos x-\sin x\mathrm{\ne }0\Rightarrow x\mathrm{\ne }\frac{\pi }{4}+\pi n$$

Это условие также можно записать как:

$$1-\mathrm{tg}x\mathrm{\ne }0\Rightarrow \mathrm{tg}x\mathrm{\ne }1$$

Таким образом, $x\mathrm{\ne }\mathrm{arctg}1+\pi n=\frac{\pi }{4}+\pi n$.

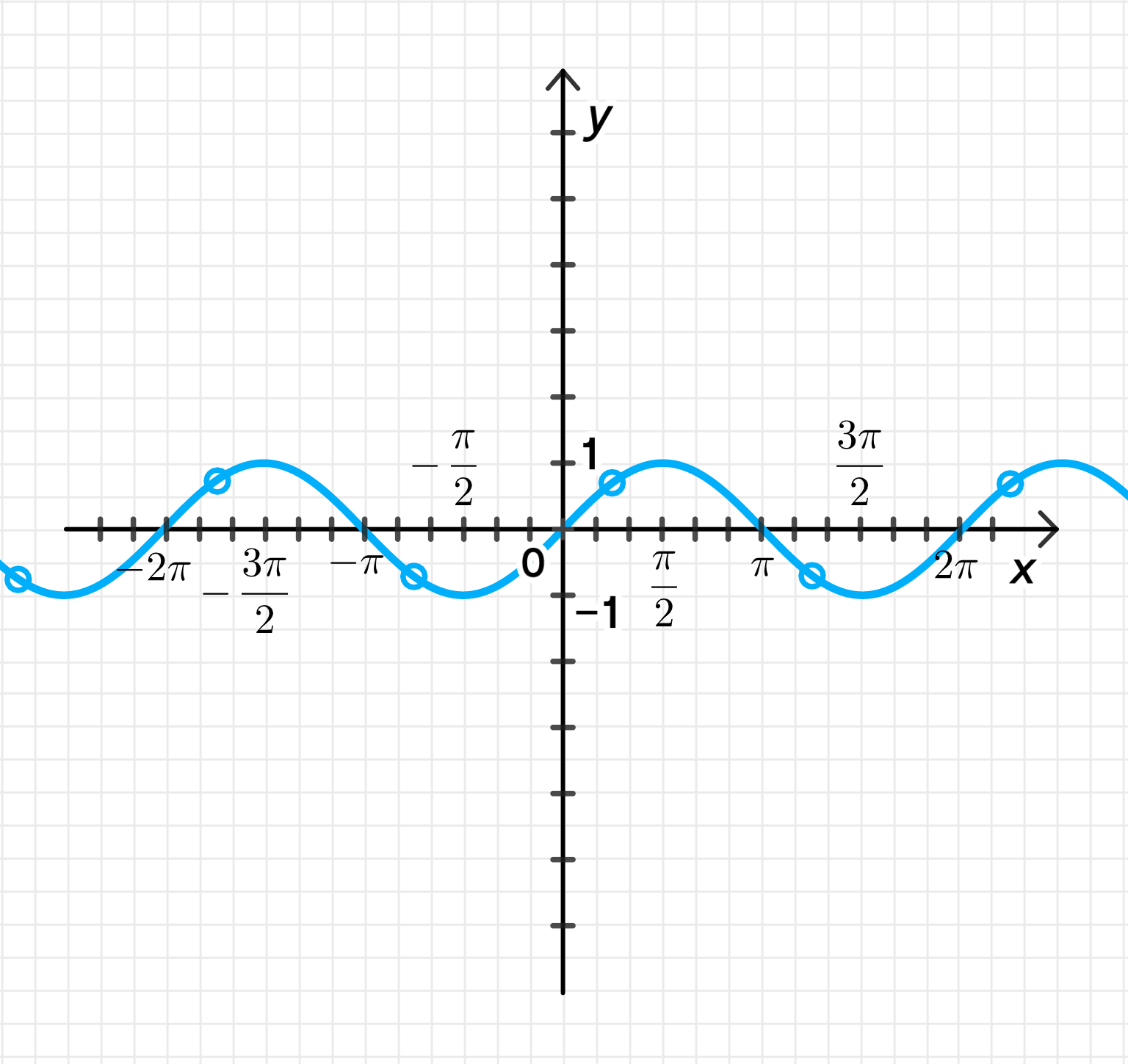
График функции:

График функции $y=\sin x$ будет представлять собой стандартную синусоиду с амплитудой 1 и периодом $2\pi$. График будет колебаться между значениями $-1$ и $1$, начиная с нуля при $x=0$, достигая максимума $1$ в $\frac{\pi }{2}$, минимума $-1$ в $\frac{3\pi }{2}$, и снова возвращаться к нулю при $2\pi$.