ГДЗ по Алгебре 10 Класс Номер 27.72 Профильный Уровень Мордкович — Подробные Ответы

а) $y = \begin{cases} 2 \sin x \cdot \cos x, & \text{если } x \leq 0 \\ 2 \sin^2 \frac{x}{4}, & \text{если } x > 0 \end{cases};$

$y = 2 \sin x \cdot \cos x = \sin 2x:$

$y = 2 \sin^2 \frac{x}{4} = 2 \cdot \frac{1 — \cos \frac{x}{2}}{2} = 1 — \cos \frac{x}{2}:$

Графики функций:

б) $y = \begin{cases} (\sin x + \cos x)^2, & \text{если } x \leq \frac{\pi}{4} \\ 2 + \frac{\pi}{4} — x, & \text{если } x > \frac{\pi}{4} \end{cases};$

$y = (\sin x + \cos x)^2 = \sin^2 x + \cos^2 x + 2 \sin x \cdot \cos x = 1 + \sin 2x:$

$y = 2 + \frac{\pi}{4} — x:$

Графики функций:

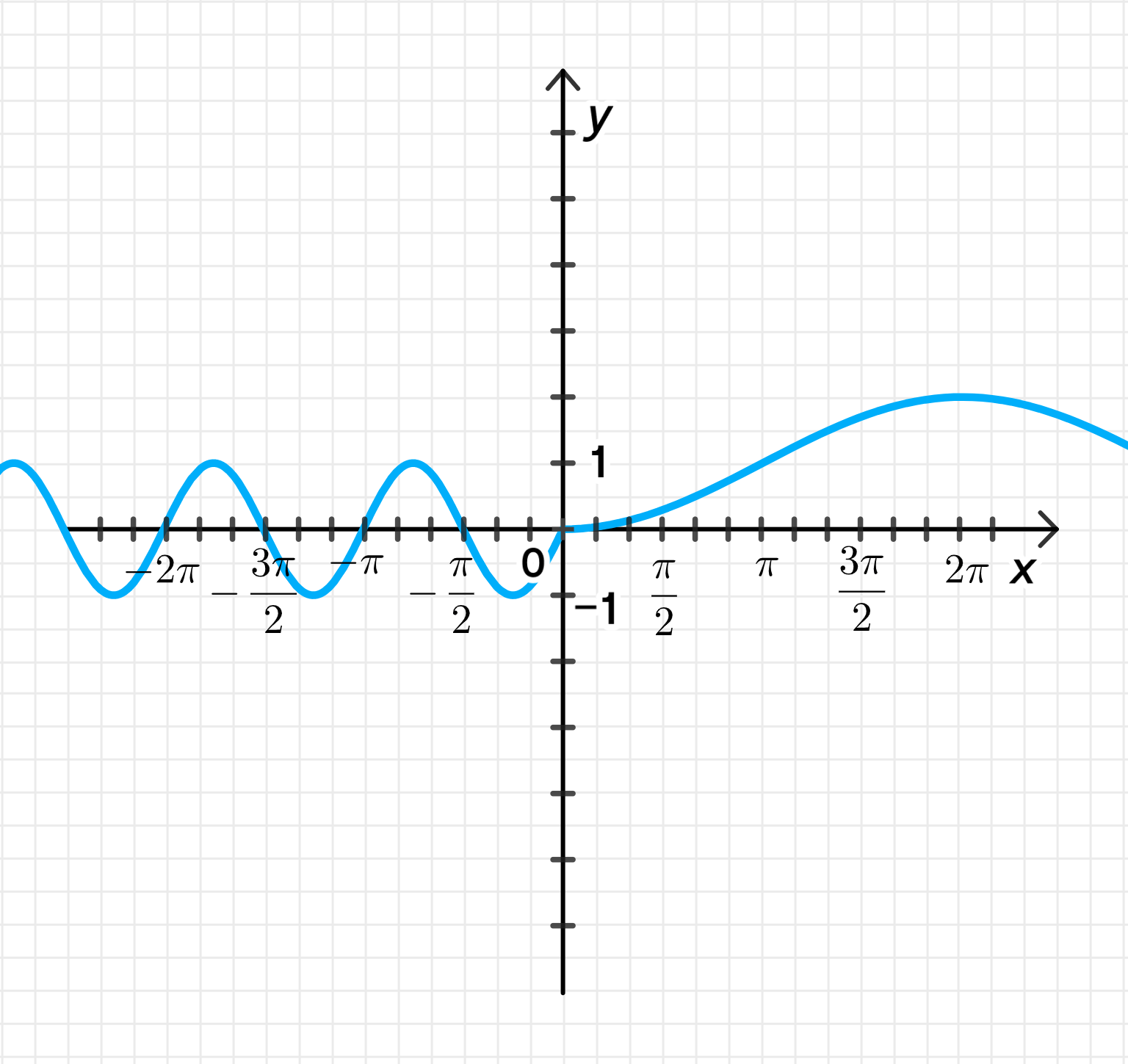
а) $y = \begin{cases} 2 \sin x \cdot \cos x, & \text{если } x \leq 0 \\ 2 \sin^2 \frac{x}{4}, & \text{если } x > 0 \end{cases};$

1) Исследование функции для $x \leq 0$:

Для $x \leq 0$ функция имеет вид:

$$y = 2 \sin x \cdot \cos x.$$

Используя тригонометрическую формулу:

$$\sin 2x = 2 \sin x \cdot \cos x,$$

мы можем выразить функцию как:

$$y = \sin 2x.$$

Теперь исследуем значения функции $y = \sin 2x$ для некоторых значений $x$:

• Для $x = -\pi$:

$$y = \sin(2(-\pi)) = \sin(-2\pi) = 0.$$

• Для $x = -\frac{3\pi}{4}$:

$$y = \sin\left(2\left(-\frac{3\pi}{4}\right)\right) = \sin\left(-\frac{3\pi}{2}\right) = 1.$$

• Для $x = -\frac{\pi}{2}$:

$$y = \sin(2(-\frac{\pi}{2})) = \sin(-\pi) = 0.$$

• Для $x = -\frac{\pi}{4}$:

$$y = \sin\left(2\left(-\frac{\pi}{4}\right)\right) = \sin\left(-\frac{\pi}{2}\right) = -1.$$

• Для $x = 0$:

$$y = \sin(2(0)) = \sin(0) = 0.$$

Таким образом, значения функции на отрезке $x \leq 0$ следующие:

2) Исследование функции для $x > 0$:

Для $x > 0$ функция имеет вид:

$$y = 2 \sin^2 \frac{x}{4}.$$

Применяя идентичность для $\sin^2 \alpha = \frac{1 — \cos 2\alpha}{2}$, получаем:

$$y = 2 \cdot \frac{1 — \cos \frac{x}{2}}{2} = 1 — \cos \frac{x}{2}.$$

Теперь исследуем значения функции $y = 1 — \cos \frac{x}{2}$ для некоторых значений $x$:

• Для $x = 0$:

$$y = 1 — \cos \left(\frac{0}{2}\right) = 1 — \cos(0) = 0.$$

• Для $x = \pi$:

$$y = 1 — \cos \left(\frac{\pi}{2}\right) = 1 — 0 = 1.$$

• Для $x = 2\pi$:

$$y = 1 — \cos \left(\frac{2\pi}{2}\right) = 1 — \cos(\pi) = 1 — (-1) = 2.$$

• Для $x = 3\pi$:

$$y = 1 — \cos \left(\frac{3\pi}{2}\right) = 1 — 0 = 1.$$

• Для $x = 4\pi$:

$$y = 1 — \cos \left(\frac{4\pi}{2}\right) = 1 — \cos(2\pi) = 0.$$

Таким образом, значения функции на отрезке $x > 0$ следующие:

3) Графики функций:

График функции $y = \sin 2x$ на интервале $x \leq 0$ будет синусоидой, проходящей через точки $(-\pi, 0)$, $\left(-\frac{3\pi}{4}, 1\right)$, $\left(-\frac{\pi}{2}, 0\right)$, $\left(-\frac{\pi}{4}, -1\right)$ и $(0, 0)$.

График функции $y = 1 — \cos \frac{x}{2}$ на интервале $x > 0$ будет иметь форму волны, проходящей через точки $(0, 0)$, $(\pi, 1)$, $(2\pi, 2)$, $(3\pi, 1)$ и $(4\pi, 0)$.

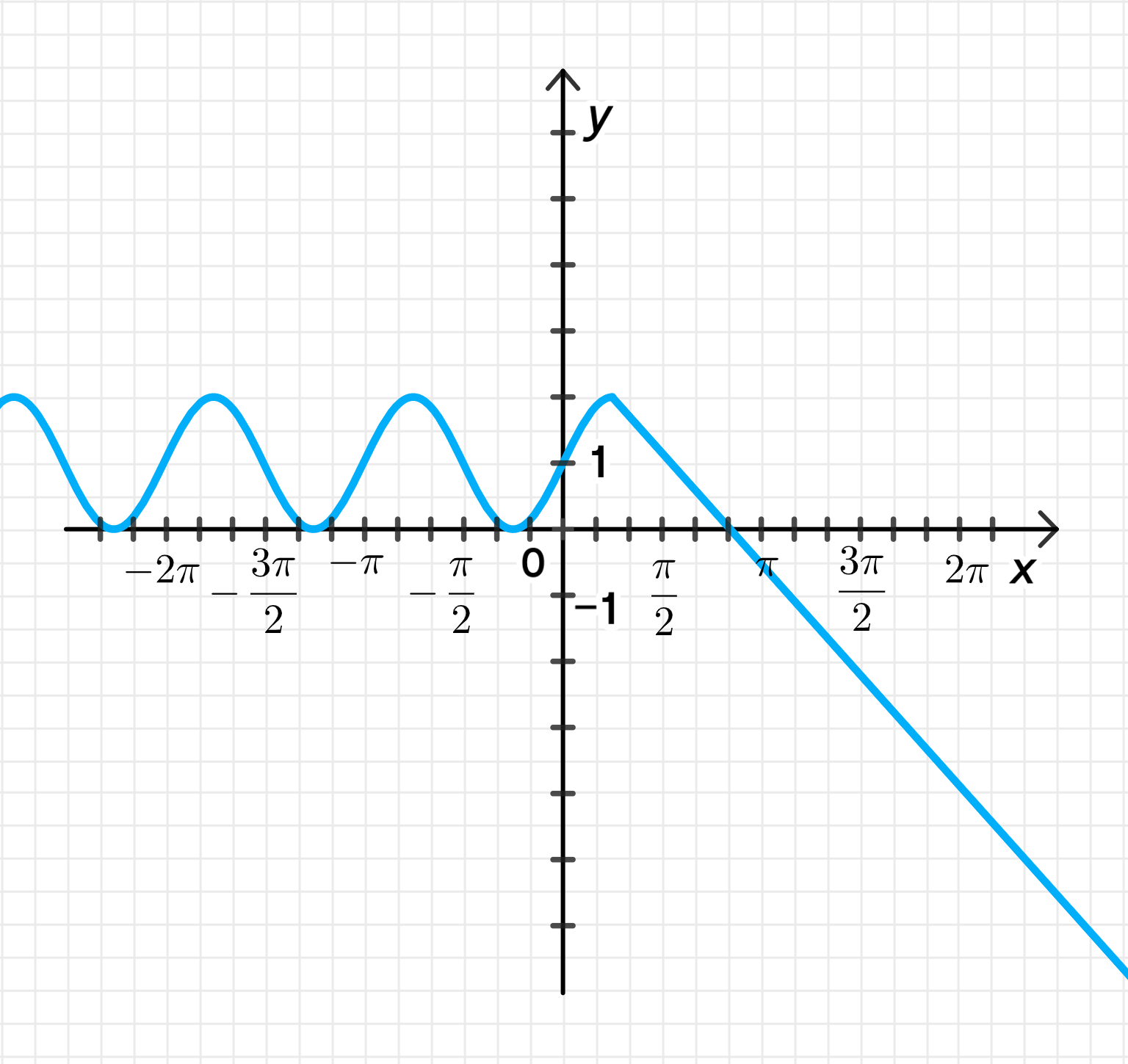
б) $y = \begin{cases} (\sin x + \cos x)^2, & \text{если } x \leq \frac{\pi}{4} \\ 2 + \frac{\pi}{4} — x, & \text{если } x > \frac{\pi}{4} \end{cases};$

1) Исследование функции для $x \leq \frac{\pi}{4}$:

Для $x \leq \frac{\pi}{4}$ функция имеет вид:

$$y = (\sin x + \cos x)^2.$$

Раскроем скобки:

$$y = \sin^2 x + \cos^2 x + 2 \sin x \cdot \cos x.$$

Используя тождество $\sin^2 x + \cos^2 x = 1$, получаем:

$$y = 1 + 2 \sin x \cdot \cos x = 1 + \sin 2x.$$

Теперь исследуем значения функции $y = 1 + \sin 2x$ для некоторых значений $x$:

• Для $x = -\frac{3\pi}{4}$:

$$y = 1 + \sin\left(2\left(-\frac{3\pi}{4}\right)\right) = 1 + \sin\left(-\frac{3\pi}{2}\right) = 2.$$

• Для $x = -\frac{\pi}{2}$:

$$y = 1 + \sin\left(2\left(-\frac{\pi}{2}\right)\right) = 1 + \sin(-\pi) = 1.$$

• Для $x = -\frac{\pi}{4}$:

$$y = 1 + \sin\left(2\left(-\frac{\pi}{4}\right)\right) = 1 + \sin\left(-\frac{\pi}{2}\right) = 0.$$

• Для $x = 0$:

$$y = 1 + \sin(0) = 1.$$

• Для $x = \frac{\pi}{4}$:

$$y = 1 + \sin\left(2\left(\frac{\pi}{4}\right)\right) = 1 + \sin\left(\frac{\pi}{2}\right) = 2.$$

Таким образом, значения функции на отрезке $x \leq \frac{\pi}{4}$ следующие:

2) Исследование функции для $x > \frac{\pi}{4}$:

Для $x > \frac{\pi}{4}$ функция имеет вид:

$$y = 2 + \frac{\pi}{4} — x.$$

Это линейная функция с отрицательным угловым коэффициентом. Исследуем значения функции:

• Для $x = \frac{\pi}{4}$:

$$y = 2 + \frac{\pi}{4} — \frac{\pi}{4} = 2.$$

• Для $x = \frac{5\pi}{3}$:

$$y = 2 + \frac{\pi}{4} — \frac{5\pi}{3} \approx 2 — 5.24 \approx -2.45.$$

Таким образом, значения функции на отрезке $x > \frac{\pi}{4}$ следующие:

3) Графики функций:

График функции $y = 1 + \sin 2x$ на интервале $x \leq \frac{\pi}{4}$ будет синусоидой, проходящей через точки $\left(-\frac{3\pi}{4}, 2\right)$, $\left(-\frac{\pi}{2}, 1\right)$, $\left(-\frac{\pi}{4}, 0\right)$, $(0, 1)$, и $\left(\frac{\pi}{4}, 2\right)$.

График функции $y = 2 + \frac{\pi}{4} — x$ на интервале $x > \frac{\pi}{4}$ будет прямой с угловым коэффициентом $-1$, проходящей через точки $\left(\frac{\pi}{4}, 2\right)$ и $\left(\frac{5\pi}{3}, -2.45\right)$.