ГДЗ по Алгебре 10 Класс Номер 28.38 Профильный Уровень Мордкович — Подробные Ответы

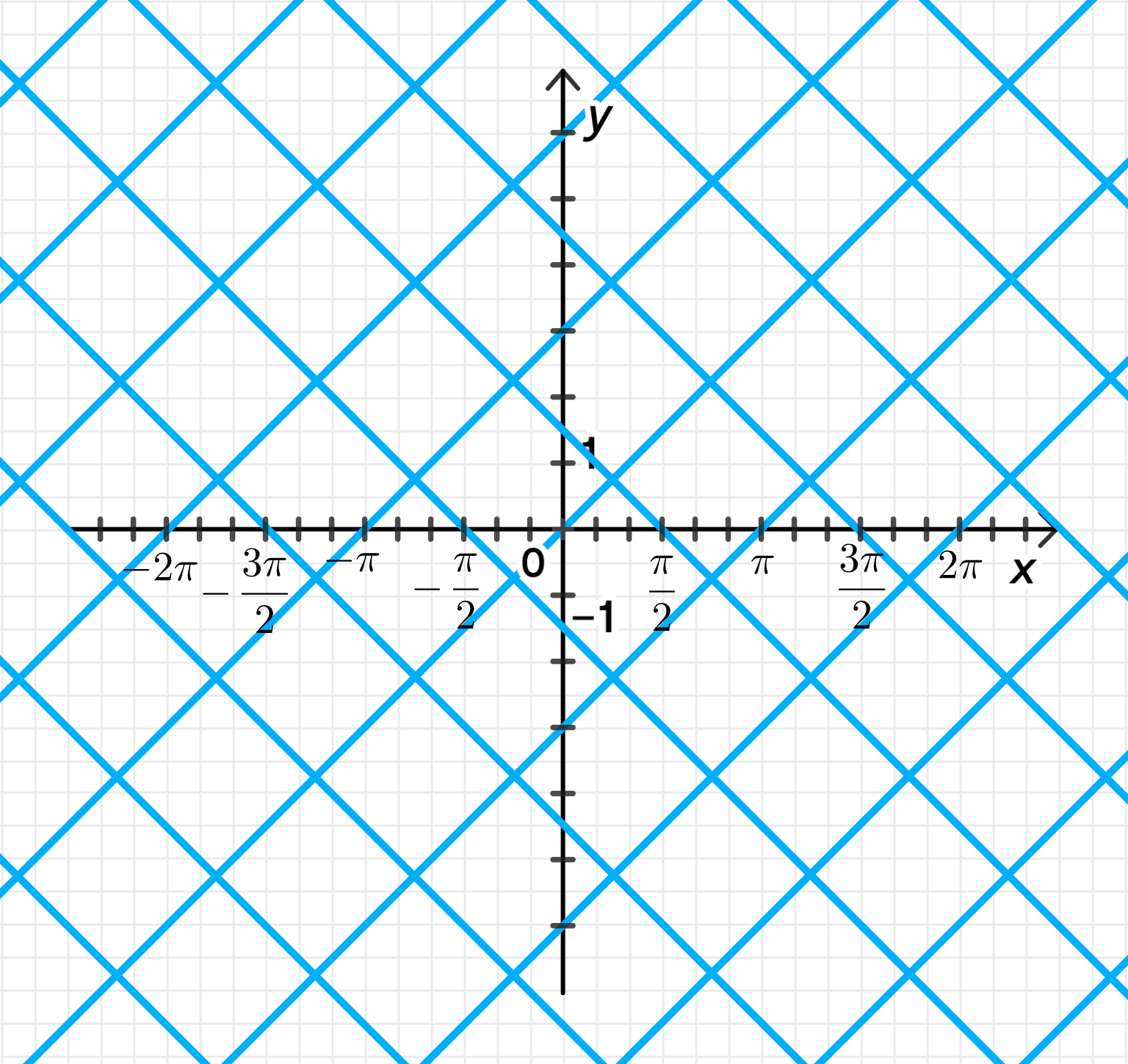
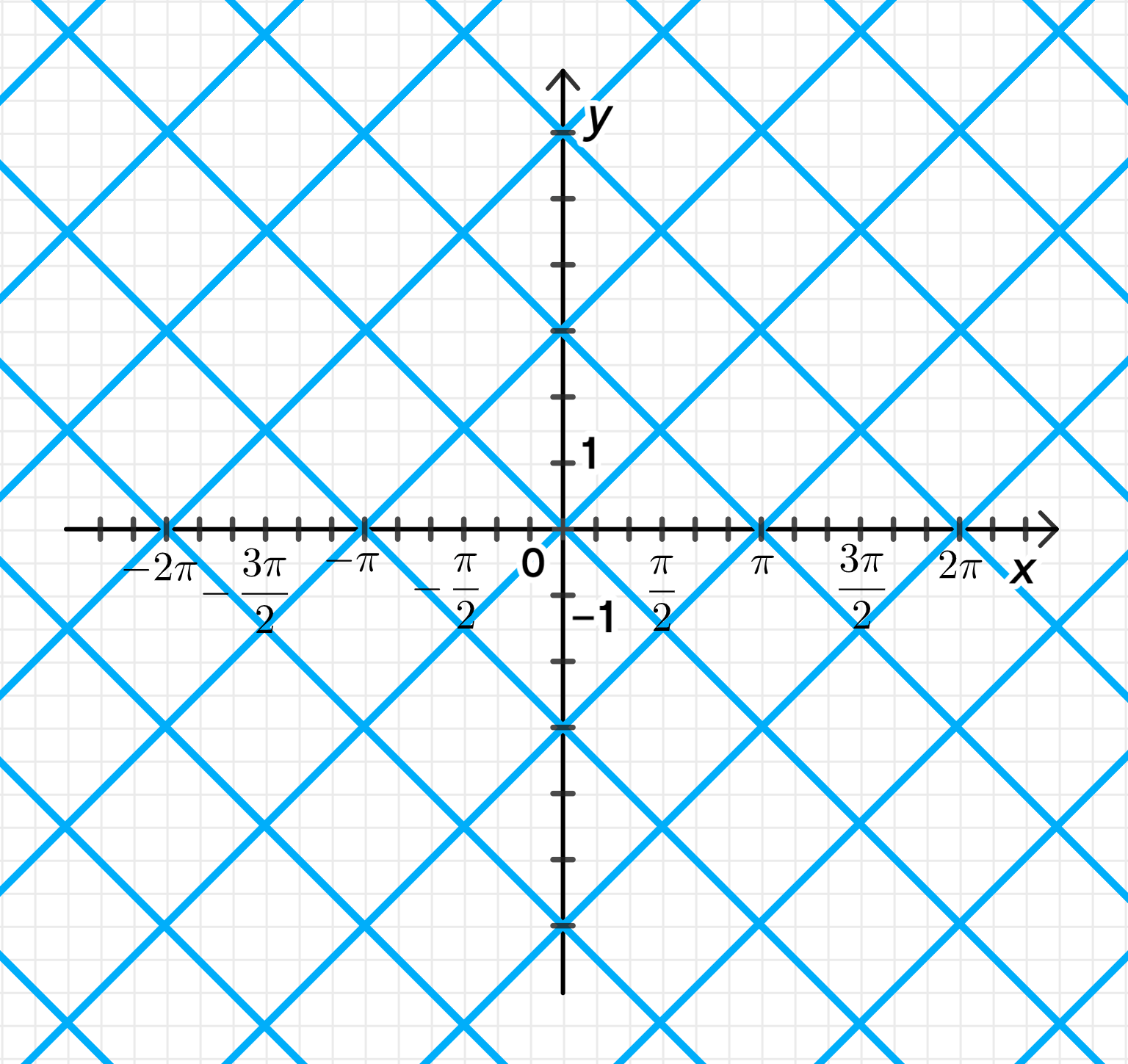
Постройте график функции:

a) sin2х = sin2у;

б) cos2х = cos2у.

a) $\sin 2x = \sin 2y$;

$$\sin 2y — \sin 2x = 0;$$ $$2 \sin \frac{2y — 2x}{2} \cdot \cos \frac{2y + 2x}{2} = 0;$$ $$\sin(y — x) \cdot \cos(y + x) = 0;$$

Первое уравнение:

$$\sin(y — x) = 0;$$ $$y — x = \pi n;$$ $$y = x + \pi n;$$

Второе уравнение:

$$\cos(y + x) = 0;$$ $$y + x = \frac{\pi}{2} + \pi n;$$ $$y = -x + \frac{\pi}{2} + \pi n;$$

График уравнения:

б) $\cos 2x = \cos 2y$;

$$\cos 2y — \cos 2x = 0;$$ $$-2 \sin \frac{2y — 2x}{2} \cdot \sin \frac{2y + 2x}{2} = 0;$$ $$\sin(y — x) \cdot \sin(y + x) = 0;$$

Первое уравнение:

$$\sin(y — x) = 0;$$ $$y — x = \pi n;$$ $$y = x + \pi n;$$

Второе уравнение:

$$\sin(y + x) = 0;$$ $$y + x = \pi n;$$ $$y = -x + \pi n;$$

График уравнения:

a) $\sin 2x = \sin 2y$

Приводим исходное уравнение к более удобному виду:

У нас есть уравнение:

$$\sin 2x = \sin 2y$$

Из свойств синуса знаем, что если две синусоиды равны, то существует два варианта: либо их аргументы равны, либо они отличаются на кратные значения $\pi$. То есть, для $\sin A = \sin B$ можно записать следующее:

$$A = B + 2k\pi \quad \text{или} \quad A = \pi — B + 2k\pi, \quad k \in \mathbb{Z}$$

Применим это к нашему уравнению:

$$2x = 2y + 2k\pi \quad \text{или} \quad 2x = \pi — 2y + 2k\pi, \quad k \in \mathbb{Z}$$

Решение для первого случая:

Для первого уравнения $2x = 2y + 2k\pi$, делим обе части на 2:

$$x = y + k\pi$$

Перепишем это:

$$y = x — k\pi$$

Таким образом, решение для этого случая — это линейная зависимость между $x$ и $y$, с постоянной разницей, которая является кратным числа $\pi$.

Решение для второго случая:

Для второго уравнения $2x = \pi — 2y + 2k\pi$, также делим обе части на 2:

$$x = \frac{\pi}{2} — y + k\pi$$

Перепишем это:

$$y = -x + \frac{\pi}{2} + k\pi$$

Это также линейное уравнение, но с другой зависимостью, где на $y$ влияют значения $x$ с дополнительной константой $\frac{\pi}{2}$.

График уравнения:

б) $\cos 2x = \cos 2y$

Приводим исходное уравнение к более удобному виду:

Итак, у нас есть уравнение:

$$\cos 2x = \cos 2y$$

Из свойств косинуса мы знаем, что для равенства косинусов существует несколько решений:

$$A = B + 2k\pi \quad \text{или} \quad A = -B + 2k\pi, \quad k \in \mathbb{Z}$$

Применим это к нашему уравнению:

$$2x = 2y + 2k\pi \quad \text{или} \quad 2x = -2y + 2k\pi, \quad k \in \mathbb{Z}$$

Решение для первого случая:

Для первого уравнения $2x = 2y + 2k\pi$, делим обе части на 2:

$$x = y + k\pi$$

Перепишем это:

$$y = x — k\pi$$

Это решение аналогично первому случаю из задачи (для синусов). Решение снова представляет собой прямую линию, где разница между $x$ и $y$ составляет $k\pi$.

Решение для второго случая:

Для второго уравнения $2x = -2y + 2k\pi$, также делим обе части на 2:

$$x = -y + k\pi$$

Перепишем это:

$$y = -x + k\pi$$

Это тоже линейное уравнение, где $y$ зависит от $x$ с наклоном -1 и пересечением на оси $y$ в точке $k\pi$.

График уравнения: