ГДЗ по Алгебре 10 Класс Номер 29.30 Профильный Уровень Мордкович — Подробные Ответы

Постройте график функции:

a) $2 \sin(x + y) \cdot \cos y = \sin x$;

б) $2 \cos(x + y) \cdot \cos x = \cos y$

a) $2 \sin(x + y) \cdot \cos y = \sin x$;

$2 \cdot \frac{\sin((x + y) + y) + \sin((x + y) — y)}{2} = \sin x$;

$\sin(x + 2y) + \sin x = \sin x$;

$\sin(x + 2y) = 0$;

$x + 2y = \pi n$;

$2y = -x + \pi n$;

$y = -0,5x + \frac{\pi n}{2}$;

График уравнения:

б) $2 \cos(x + y) \cdot \cos x = \cos y$;

$2 \cdot \frac{\cos((x + y) + x) + \cos((x + y) — x)}{2} = \cos y$;

$\cos(2x + y) + \cos y = \cos y$;

$\cos(2x + y) = 0$;

$2x + y = \frac{\pi}{2} + \pi n$;

$y = -2x + \frac{\pi}{2} + \pi n$;

График уравнения:

а) $2 \sin(x + y) \cdot \cos y = \sin x$

Начнем с преобразования выражения:

Исходное уравнение:

$$2 \sin(x + y) \cdot \cos y = \sin x$$

Применим тригонометрическую формулу для произведения синуса и косинуса:

$$2 \sin A \cos B = \sin(A + B) + \sin(A — B)$$

где $A = x + y$ и $B = y$. Подставим в формулу:

$$2 \sin(x + y) \cdot \cos y = \sin((x + y) + y) + \sin((x + y) — y)$$

Подставим выражения:

Получаем:

$$\sin(x + 2y) + \sin(x) = \sin x$$

Теперь можно упростить, так как $\sin x$ с обеих сторон уравнения.

Упростим уравнение:

Убираем $\sin x$ с обеих сторон:

$$\sin(x + 2y) = 0$$

Решаем уравнение $\sin(x + 2y) = 0$:

Синус равен нулю, когда его аргумент кратен $\pi$, то есть:

$$x + 2y = \pi n, \quad n \in \mathbb{Z}$$

Решаем относительно $y$:

Из уравнения $x + 2y = \pi n$ выразим $y$:

$$2y = -x + \pi n$$ $$y = -0,5x + \frac{\pi n}{2}$$

Таким образом, мы получаем общее решение для $y$.

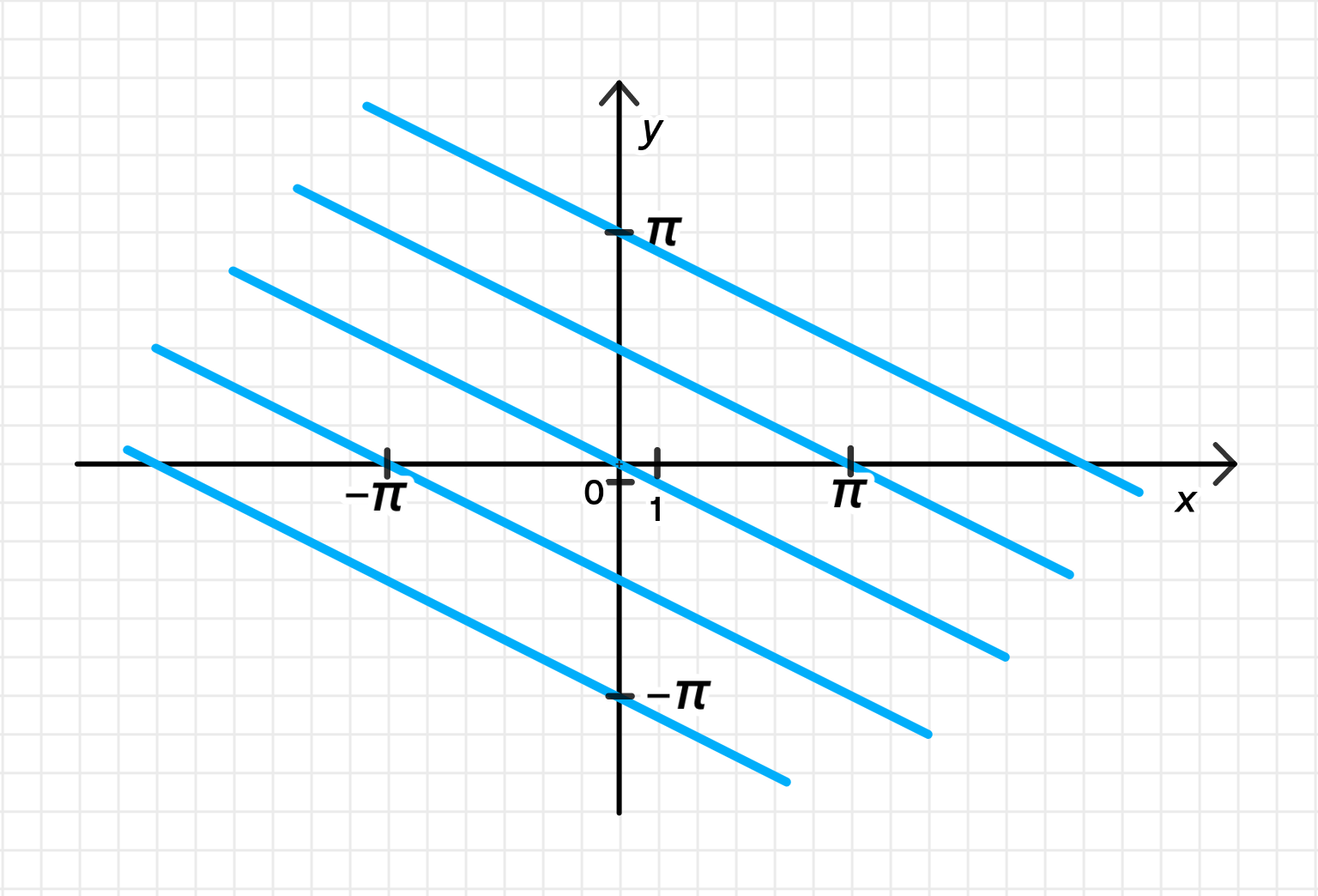
График уравнения:

Уравнение $y = -0,5x + \frac{\pi n}{2}$ представляет собой семейство прямых с угловым коэффициентом $-0,5$ и смещением, которое зависит от значения $n$. Для каждого значения $n$ будет получаться своя прямая.

б) $2 \cos(x + y) \cdot \cos x = \cos y$

Начнем с преобразования выражения:

Исходное уравнение:

$$2 \cos(x + y) \cdot \cos x = \cos y$$

Применим аналогичную формулу для произведения косинуса:

$$2 \cos A \cos B = \cos(A + B) + \cos(A — B)$$

где $A = x + y$ и $B = x$. Подставим в формулу:

$$2 \cos(x + y) \cdot \cos x = \cos((x + y) + x) + \cos((x + y) — x)$$

Подставим выражения:

Получаем:

$$\cos(2x + y) + \cos y = \cos y$$

Теперь можно упростить, так как $\cos y$ с обеих сторон уравнения.

Упростим уравнение:

Убираем $\cos y$ с обеих сторон:

$$\cos(2x + y) = 0$$

Решаем уравнение $\cos(2x + y) = 0$:

Косинус равен нулю, когда его аргумент равен $\frac{\pi}{2} + \pi n$, где $n$ — целое число:

$$2x + y = \frac{\pi}{2} + \pi n, \quad n \in \mathbb{Z}$$

Решаем относительно $y$:

Из уравнения $2x + y = \frac{\pi}{2} + \pi n$ выразим $y$:

$$y = -2x + \frac{\pi}{2} + \pi n$$

Таким образом, мы получаем общее решение для $y$.

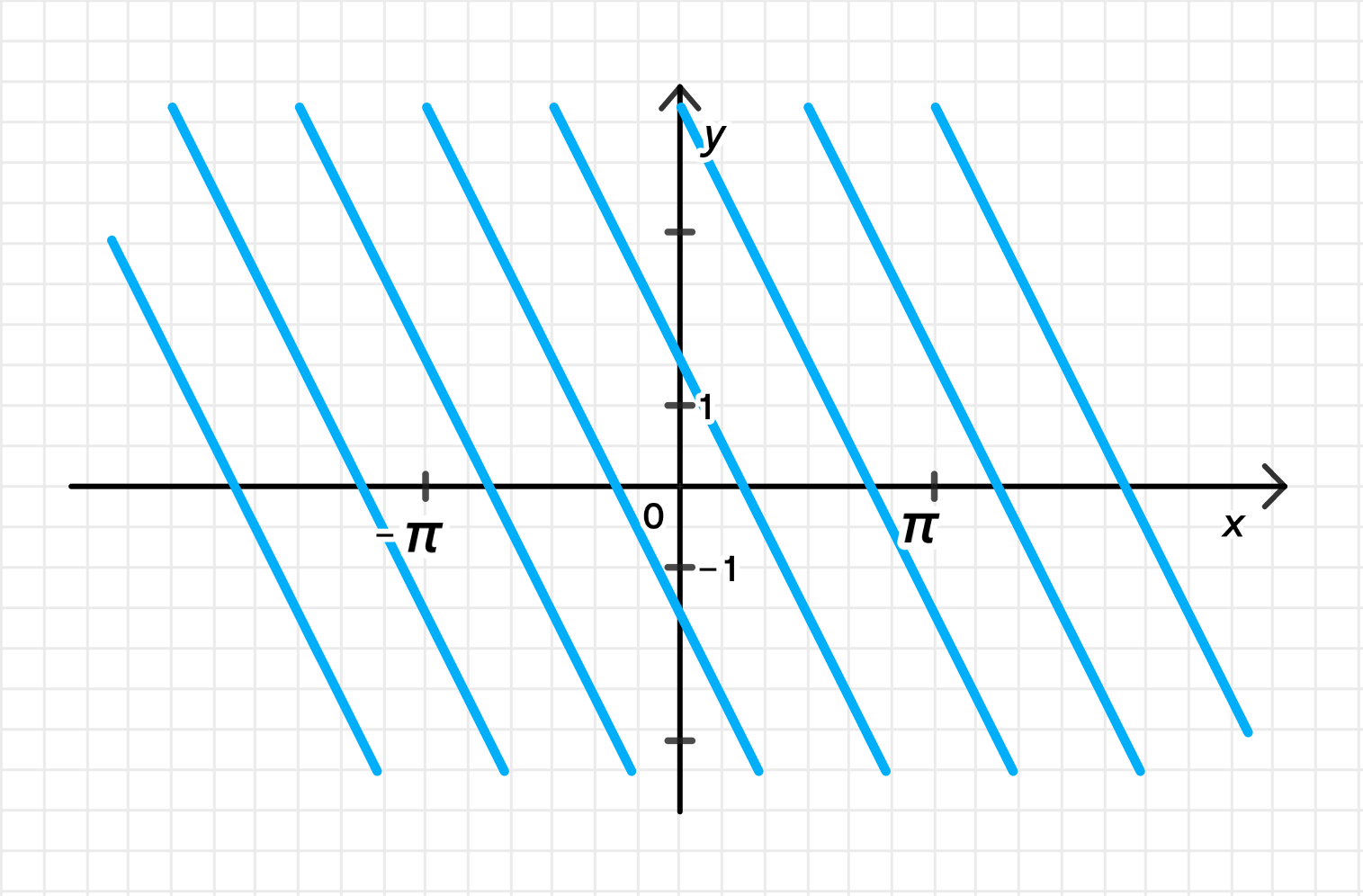
График уравнения:

Уравнение $y = -2x + \frac{\pi}{2} + \pi n$ также представляет собой семейство прямых. Для каждого значения $n$ будет получаться своя прямая с угловым коэффициентом $-2$ и смещением, которое зависит от значения $n$.

$$y = -2x + \frac{\pi}{2} + \pi n$$