ГДЗ по Алгебре 10 Класс Номер 29.31 Профильный Уровень Мордкович — Подробные Ответы

Постройте график функции:

а) $\cos \frac{x(y-1)}{2} \cdot \cos \frac{x(y+1)}{2} = \cos^2 \frac{x}{2}$;

б) $\sin \frac{y(x+1)}{2} \cdot \cos \frac{y(x-1)}{2} = \cos^2 \left( \frac{\pi}{4} — \frac{y}{2} \right)$

а) $\cos \frac{x(y-1)}{2} \cdot \cos \frac{x(y+1)}{2} = \cos^2 \frac{x}{2}$;

$$\frac{\cos \left( \frac{x(y+1)}{2} + \frac{x(y-1)}{2} \right) + \cos \left( \frac{x(y+1)}{2} — \frac{x(y-1)}{2} \right)}{2} = \frac{1 + \cos \frac{2x}{2}}{2};$$ $$\cos xy + \cos x = 1 + \cos x;$$ $$\cos xy = 1;$$ $$xy = 2\pi n;$$ $$x = 0, \ y = 0, \ y = \frac{2\pi n}{x};$$

График уравнения:

б) $\sin \frac{y(x+1)}{2} \cdot \cos \frac{y(x-1)}{2} = \cos^2 \left( \frac{\pi}{4} — \frac{y}{2} \right)$;

$$\frac{\sin \left( \frac{y(x+1)}{2} + \frac{y(x-1)}{2} \right) + \sin \left( \frac{y(x+1)}{2} — \frac{y(x-1)}{2} \right)}{2} = \frac{1 + \cos 2 \left( \frac{\pi}{4} — \frac{y}{2} \right)}{2};$$ $$\sin xy + \sin y = 1 + \cos \left( \frac{\pi}{2} — y \right);$$ $$\sin xy + \sin y = 1 + \sin y;$$ $$\sin xy = 1;$$ $$xy = \frac{\pi}{2} + \pi n;$$ $$xy = \frac{\pi + 2\pi n}{2};$$ $$y = \frac{\pi + 2\pi n}{2x};$$

График уравнения:

а) $\cos \frac{x(y-1)}{2} \cdot \cos \frac{x(y+1)}{2} = \cos^2 \frac{x}{2}$

Шаг 1: Применим тригонометрическую формулу для произведения косинусов.

Мы знаем, что для произведения косинусов существует следующая тригонометрическая формула:

$$2 \cos A \cdot \cos B = \cos(A + B) + \cos(A — B)$$

Здесь $A = \frac{x(y-1)}{2}$ и $B = \frac{x(y+1)}{2}$.

Применяя формулу, получаем:

$$\cos \frac{x(y-1)}{2}\cdot \cos \frac{x(y+1)}{2}=\frac{1}{2}[\cos (\frac{x(y-1)}{2}+\frac{x(y+1)}{2})+$$

$$\cos \frac{x(y-1)}{2} \cdot \cos \frac{x(y+1)}{2} = \frac{1}{2} \left[ \cos \left( \frac{x(y-1)}{2} + \frac{x(y+1)}{2} \right) + \cos \left( \frac{x(y-1)}{2} — \frac{x(y+1)}{2} \right) \right]$$

Шаг 2: Упростим выражения в косинусах.

Начнем с упрощения выражений внутри косинусов. Первое:

$$\frac{x(y-1)}{2} + \frac{x(y+1)}{2} = \frac{x(y-1 + y+1)}{2} = \frac{2xy}{2} = xy$$

Второе выражение:

$$\frac{x(y-1)}{2} — \frac{x(y+1)}{2} = \frac{x(y-1 — (y+1))}{2} = \frac{x(-2)}{2} = -x$$

Таким образом, выражение для произведения косинусов превращается в:

$$\frac{1}{2} \left[ \cos(xy) + \cos(-x) \right]$$

Так как $\cos(-x) = \cos(x)$, мы получаем:

$$\frac{1}{2} \left[ \cos(xy) + \cos(x) \right]$$

Шаг 3: Сравним с правой частью уравнения.

Правая часть уравнения:

$$\cos^2 \frac{x}{2}$$

Используем формулу для $\cos^2 A = \frac{1 + \cos 2A}{2}$, подставим $A = \frac{x}{2}$:

$$\cos^2 \frac{x}{2} = \frac{1 + \cos x}{2}$$

Теперь у нас есть следующее уравнение:

$$\frac{1}{2} \left[ \cos(xy) + \cos(x) \right] = \frac{1 + \cos x}{2}$$

Шаг 4: Упростим уравнение.

Умножим обе стороны на 2, чтобы избавиться от дробей:

$$\cos(xy) + \cos(x) = 1 + \cos(x)$$

Теперь вычтем $\cos(x)$ с обеих сторон:

$$\cos(xy) = 1$$

Шаг 5: Решим уравнение $\cos(xy) = 1$.

Косинус равен 1, когда его аргумент равен $2\pi n$, где $n$ — целое число. То есть:

$$xy = 2\pi n$$

Шаг 6: Извлечем $y$.

Теперь, если $xy = 2\pi n$, то можно выразить $y$:

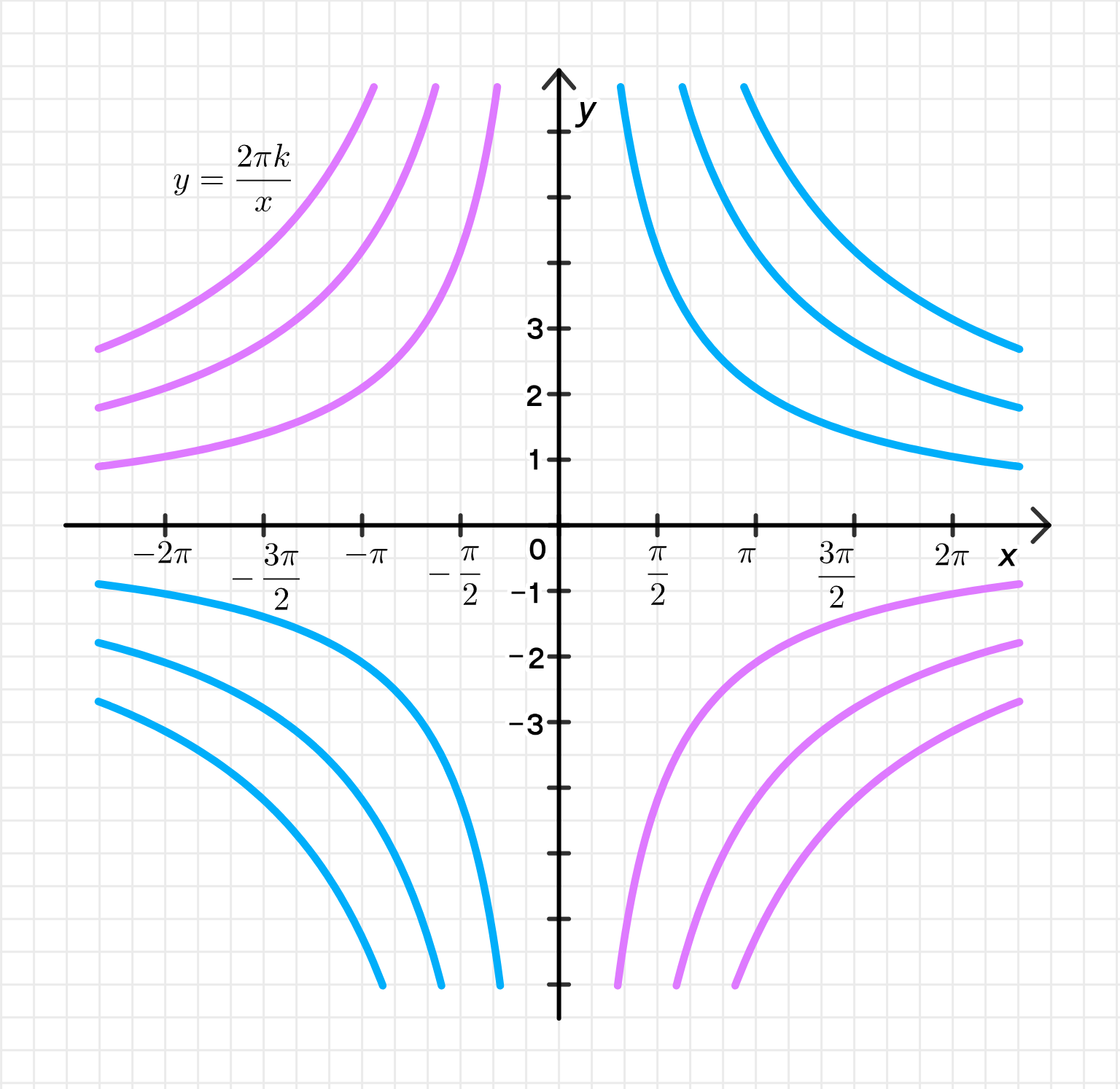
$$y = \frac{2\pi n}{x}$$

Шаг 7: Особые случаи.

Если $x = 0$, то у нас $y = 0$, так как $2\pi n / 0$ не имеет смысла.

Итак, общие решения:

$$x = 0, \ y = 0, \ y = \frac{2\pi n}{x}$$

График уравнения:

б) $\sin \frac{y(x+1)}{2} \cdot \cos \frac{y(x-1)}{2} = \cos^2 \left( \frac{\pi}{4} — \frac{y}{2} \right)$

Шаг 1: Применим тригонометрическую формулу для произведения синуса и косинуса.

Используем формулу для произведения синуса и косинуса:

$$2 \sin A \cdot \cos B = \sin(A + B) + \sin(A — B)$$

Здесь $A = \frac{y(x+1)}{2}$ и $B = \frac{y(x-1)}{2}$.

Применяя формулу, получаем:

$$\sin \frac{y(x+1)}{2}\cdot \cos \frac{y(x-1)}{2}=\frac{1}{2}[\sin (\frac{y(x+1)}{2}+\frac{y(x-1)}{2})+$$

$$\sin \frac{y(x+1)}{2} \cdot \cos \frac{y(x-1)}{2} = \frac{1}{2} \left[ \sin \left( \frac{y(x+1)}{2} + \frac{y(x-1)}{2} \right) + \sin \left( \frac{y(x+1)}{2} — \frac{y(x-1)}{2} \right) \right]$$

Шаг 2: Упростим выражения внутри синусов.

Первое:

$$\frac{y(x+1)}{2} + \frac{y(x-1)}{2} = \frac{y(x+1 + x-1)}{2} = \frac{2xy}{2} = xy$$

Второе:

$$\frac{y(x+1)}{2} — \frac{y(x-1)}{2} = \frac{y(x+1 — (x-1))}{2} = \frac{y(2)}{2} = y$$

Таким образом, произведение синуса и косинуса преобразуется в:

$$\frac{1}{2} \left[ \sin(xy) + \sin(y) \right]$$

Шаг 3: Сравним с правой частью уравнения.

Правая часть уравнения:

$$\cos^2 \left( \frac{\pi}{4} — \frac{y}{2} \right)$$

Используем формулу $\cos^2 A = \frac{1 + \cos 2A}{2}$ и подставляем $A = \frac{\pi}{4} — \frac{y}{2}$:

$$\cos^2 \left( \frac{\pi}{4} — \frac{y}{2} \right) = \frac{1 + \cos \left( \pi — y \right)}{2}$$

Так как $\cos(\pi — y) = -\cos y$, получаем:

$$\cos^2 \left( \frac{\pi}{4} — \frac{y}{2} \right) = \frac{1 — \cos y}{2}$$

Шаг 4: Сравним обе части уравнения.

Теперь у нас есть уравнение:

$$\frac{1}{2} \left[ \sin(xy) + \sin(y) \right] = \frac{1 — \cos y}{2}$$

Умножим обе стороны на 2:

$$\sin(xy) + \sin(y) = 1 — \cos y$$

Шаг 5: Упростим уравнение.

Из $1 — \cos y = \sin^2 \frac{y}{2}$, у нас:

$$\sin(xy) + \sin(y) = \sin^2 \frac{y}{2}$$

Шаг 6: Решим уравнение.

Решение получается из $\sin(xy) = 1$, что приводит к:

$$xy = \frac{\pi}{2} + \pi n$$

Шаг 7: Выразим $y$.

Из $xy = \frac{\pi}{2} + \pi n$ получаем:

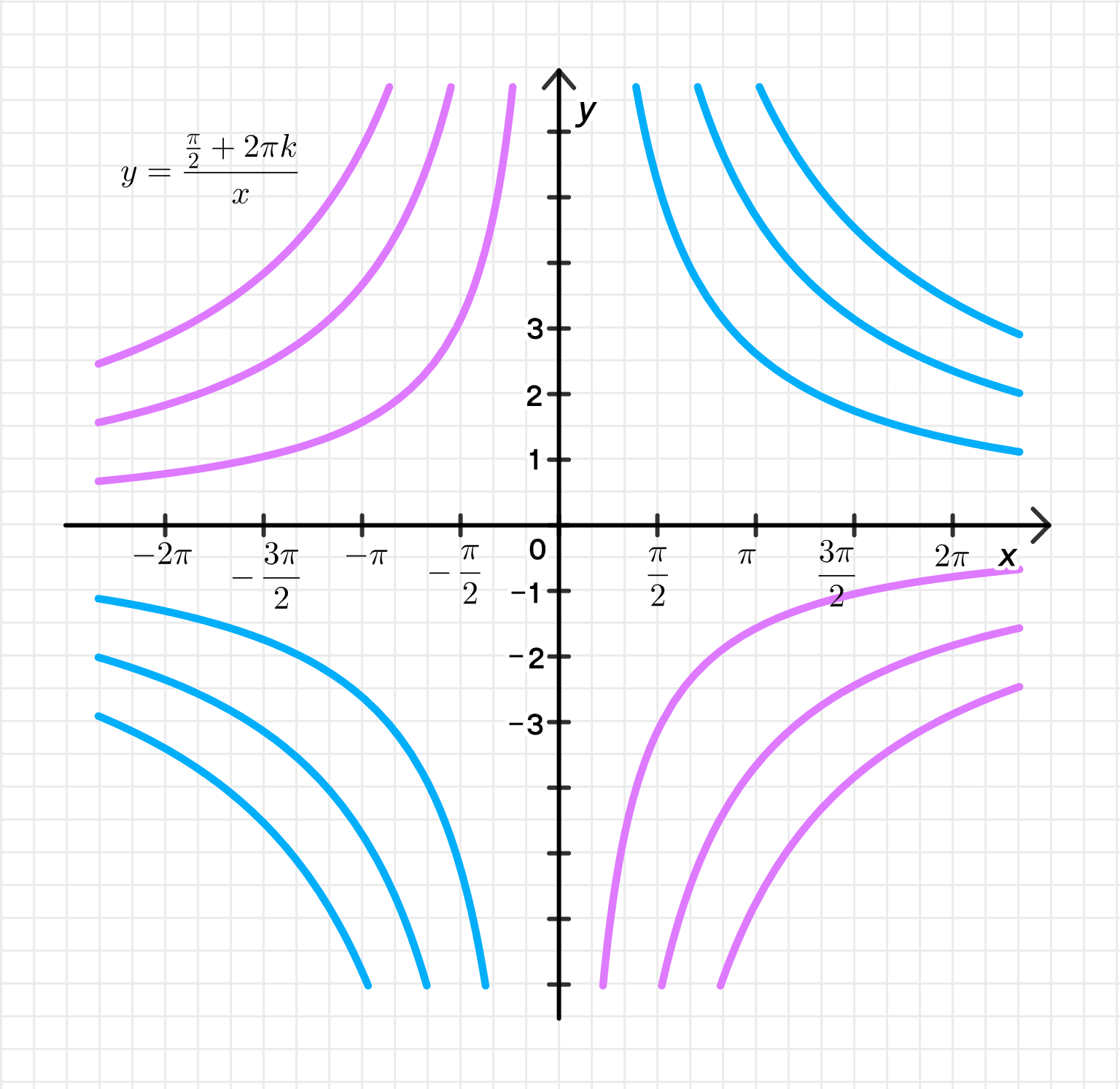
$$y = \frac{\pi + 2\pi n}{2x}$$

График уравнения:

$$y = \frac{\pi + 2\pi n}{2x}$$