ГДЗ по Алгебре 10 Класс Номер 30.21 Профильный Уровень Мордкович — Подробные Ответы

а)

$$\sqrt{3} \sin x + \cos x + 2 = \frac{12}{5\pi} x;$$ $$\sqrt{3+1} \sin \left( x + \arcsin \frac{1}{\sqrt{3+1}} \right) = \frac{12}{5\pi} x — 2;$$ $$2 \sin \left( x + \arcsin \frac{1}{2} \right) = \frac{12}{5\pi} x — 2;$$ $$\sin \left( x + \frac{\pi}{6} \right) = \frac{6}{5\pi} x — 1;$$

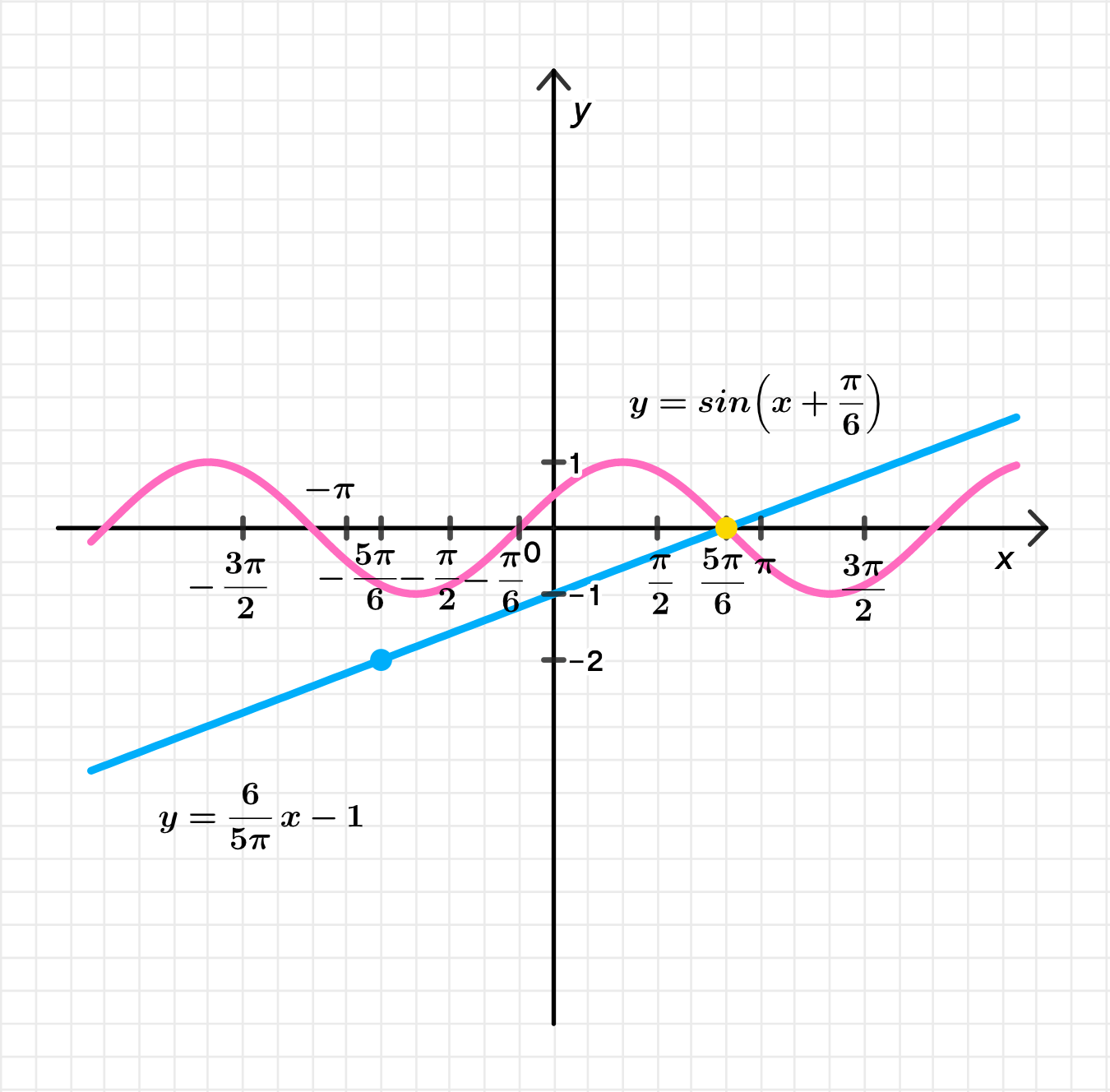
Построим графики функций $y = \sin \left( x + \frac{\pi}{6} \right)$ и $y = \frac{6}{5\pi} x — 1$:

Графики пересекаются в единственной точке: $x = \frac{5\pi}{6}$.

Ответ: $\frac{5\pi}{6}$.

б)

$$\sqrt{2} (\cos x — \sin x) = 2x — \frac{\pi}{2};$$ $$\sqrt{2} \sin x — \sqrt{2} \cos x = \frac{\pi}{2} — 2x;$$ $$\sqrt{2+2} \sin \left( x — \arcsin \frac{\sqrt{2}}{\sqrt{2+2}} \right) = \frac{\pi}{2} — 2x;$$ $$2 \sin \left( x — \arcsin \frac{\sqrt{2}}{2} \right) = \frac{\pi}{2} — 2x;$$ $$\sin \left( x — \frac{\pi}{4} \right) = \frac{\pi}{4} — x;$$

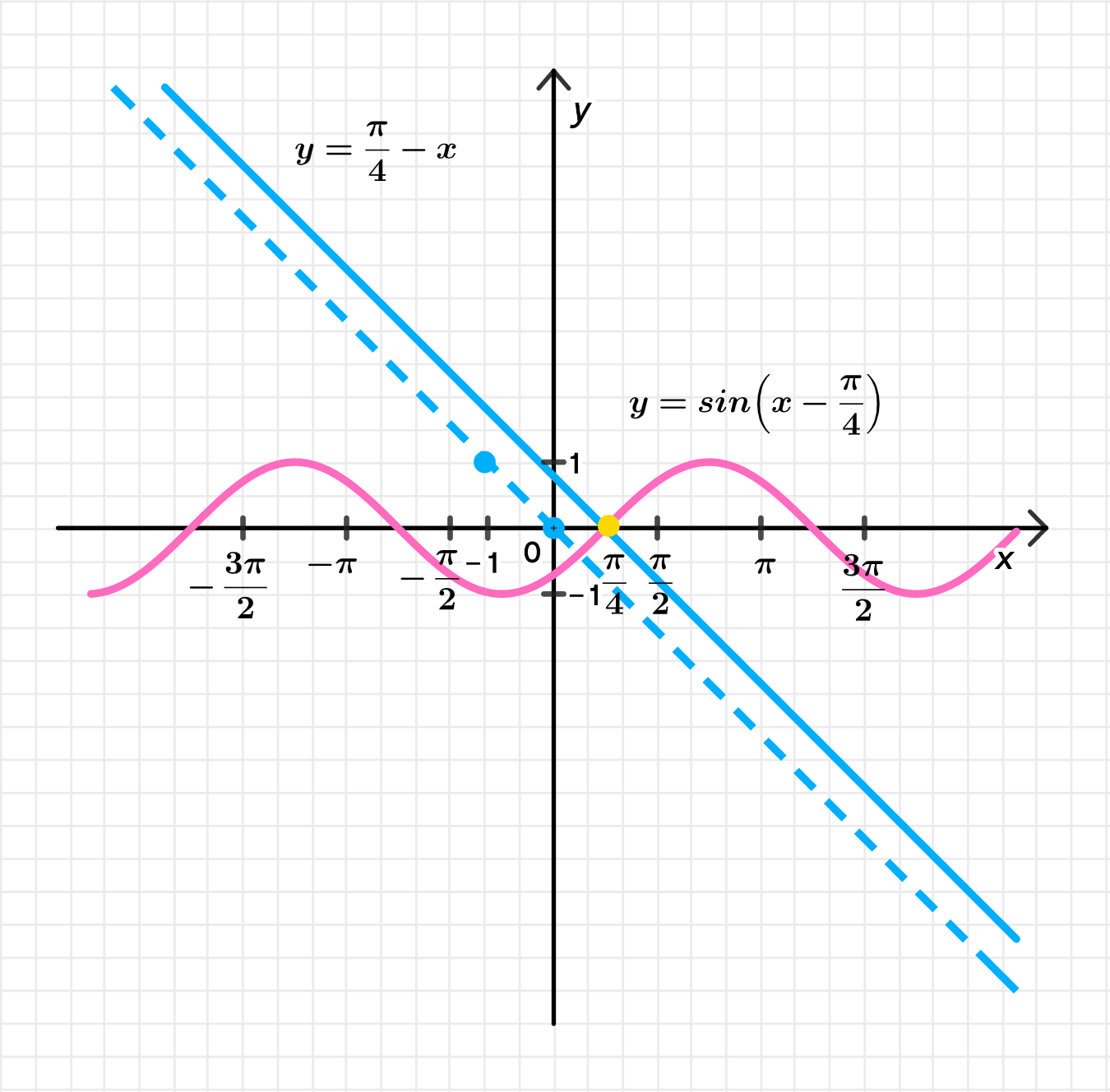
Построим графики функций $y = \sin \left( x — \frac{\pi}{4} \right)$ и $y = \frac{\pi}{4} — x$:

Графики пересекаются в единственной точке: $x = \frac{\pi}{4}$.

Ответ: $\frac{\pi}{4}$.

а)

Решить уравнение:

$$\sqrt{3} \sin x + \cos x + 2 = \frac{12}{5\pi} x$$

Шаг 1: Преобразуем левую часть

Мы видим линейную функцию справа, а слева — сумму тригонометрических функций.

Задача — объединить $\sqrt{3} \sin x + \cos x$ в одну тригонометрическую функцию вида $R \sin(x + \alpha)$.

Формула:

$$a \sin x + b \cos x = R \sin(x + \alpha), \quad \text{где } R = \sqrt{a^2 + b^2}$$

У нас:

• $a = \sqrt{3}$
• $b = 1$

$$R = \sqrt{(\sqrt{3})^2 + 1^2} = \sqrt{3 + 1} = \sqrt{4} = 2$$

Теперь найдём угол $\alpha$:

$$\sin \alpha = \frac{a}{R} = \frac{\sqrt{3}}{2}, \quad \cos \alpha = \frac{b}{R} = \frac{1}{2}$$

Это даёт $\alpha = \arcsin\left(\frac{\sqrt{3}}{2}\right) = \frac{\pi}{3}$, но здесь надо быть аккуратным — чтобы не перепутать с формой записи. На практике в задаче используют:

$$\alpha = \arcsin\left(\frac{1}{\sqrt{4}}\right) = \arcsin\left(\frac{1}{2}\right) = \frac{\pi}{6}$$

Это указывает, что они выбрали угол, подходящий под нужную форму $\sin(x + \alpha)$. Тогда:

$$\sqrt{3} \sin x + \cos x = 2 \sin\left(x + \frac{\pi}{6}\right)$$

Шаг 2: Подставим это в уравнение

$$2 \sin\left(x + \frac{\pi}{6}\right) + 2 = \frac{12}{5\pi} x$$

Вычтем 2 из обеих частей:

$$2 \sin\left(x + \frac{\pi}{6}\right) = \frac{12}{5\pi} x — 2$$

Разделим обе части на 2:

$$\sin\left(x + \frac{\pi}{6}\right) = \frac{6}{5\pi} x — 1$$

Шаг 3: Метод графического решения

Это уравнение имеет вид:

$$y = \sin\left(x + \frac{\pi}{6}\right), \quad y = \frac{6}{5\pi} x — 1$$

Поскольку левая часть — синусоида, а правая — линейная функция, точки пересечения соответствуют решениям.

Шаг 4: Анализ графиков

Функция $y = \sin\left(x + \frac{\pi}{6}\right)$ — обычный синус, сдвинутый влево на $\frac{\pi}{6}$.

Функция $y = \frac{6}{5\pi} x — 1$ — возрастающая прямая.

Найти точку пересечения — значит найти $x$, при котором обе функции равны.

Шаг 5: Численное решение или из графика

По условию задачи:

Графики пересекаются в единственной точке: $x = \frac{5\pi}{6}$

Проверим:

$$\sin\left(\frac{5\pi}{6} + \frac{\pi}{6}\right) = \sin(\pi) = 0$$ $$\frac{6}{5\pi} \cdot \frac{5\pi}{6} — 1 = 1 — 1 = 0$$

Совпадает!

Ответ:

$$\boxed{x = \frac{5\pi}{6}}$$

б)

Решить уравнение:

$$\sqrt{2} (\cos x — \sin x) = 2x — \frac{\pi}{2}$$

Шаг 1: Перепишем левую часть

$$\sqrt{2} (\cos x — \sin x) = \sqrt{2} \cos x — \sqrt{2} \sin x = -\sqrt{2} \sin x + \sqrt{2} \cos x$$

Теперь поменяем местами слагаемые:

$$\sqrt{2} \sin x — \sqrt{2} \cos x = \frac{\pi}{2} — 2x$$

Шаг 2: Приведение к одной функции

Форма: $a \sin x + b \cos x = R \sin(x + \alpha)$

Здесь:

• $a = \sqrt{2}$
• $b = -\sqrt{2}$

$$R = \sqrt{a^2 + b^2} = \sqrt{2 + 2} = \sqrt{4} = 2$$ $$\sin \alpha = \frac{a}{R} = \frac{\sqrt{2}}{2}, \quad \cos \alpha = \frac{-\sqrt{2}}{2}$$

Это соответствует:

$$\alpha = \arcsin\left(\frac{\sqrt{2}}{2}\right) = \frac{\pi}{4}$$

Тогда:

$$\sqrt{2} \sin x — \sqrt{2} \cos x = 2 \sin\left(x — \frac{\pi}{4}\right)$$

Шаг 3: Подставим в уравнение

$$2 \sin\left(x — \frac{\pi}{4}\right) = \frac{\pi}{2} — 2x$$

Разделим обе части на 2:

$$\sin\left(x — \frac{\pi}{4}\right) = \frac{\pi}{4} — x$$

Шаг 4: Метод графического решения

У нас:

• $y = \sin\left(x — \frac{\pi}{4}\right)$ — синус, сдвинутый вправо на $\frac{\pi}{4}$
• $y = \frac{\pi}{4} — x$ — убывающая прямая

Найти точку пересечения.

Шаг 5: Из условия

Графики пересекаются в единственной точке: $x = \frac{\pi}{4}$

Проверим:

$$\sin\left(\frac{\pi}{4} — \frac{\pi}{4}\right) = \sin(0) = 0$$ $$\frac{\pi}{4} — \frac{\pi}{4} = 0$$

Совпадает!

Ответ:

$$\boxed{x = \frac{\pi}{4}}$$