ГДЗ по Алгебре 10 Класс Номер 30.9 Профильный Уровень Мордкович — Подробные Ответы

Постройте график функции:

а)

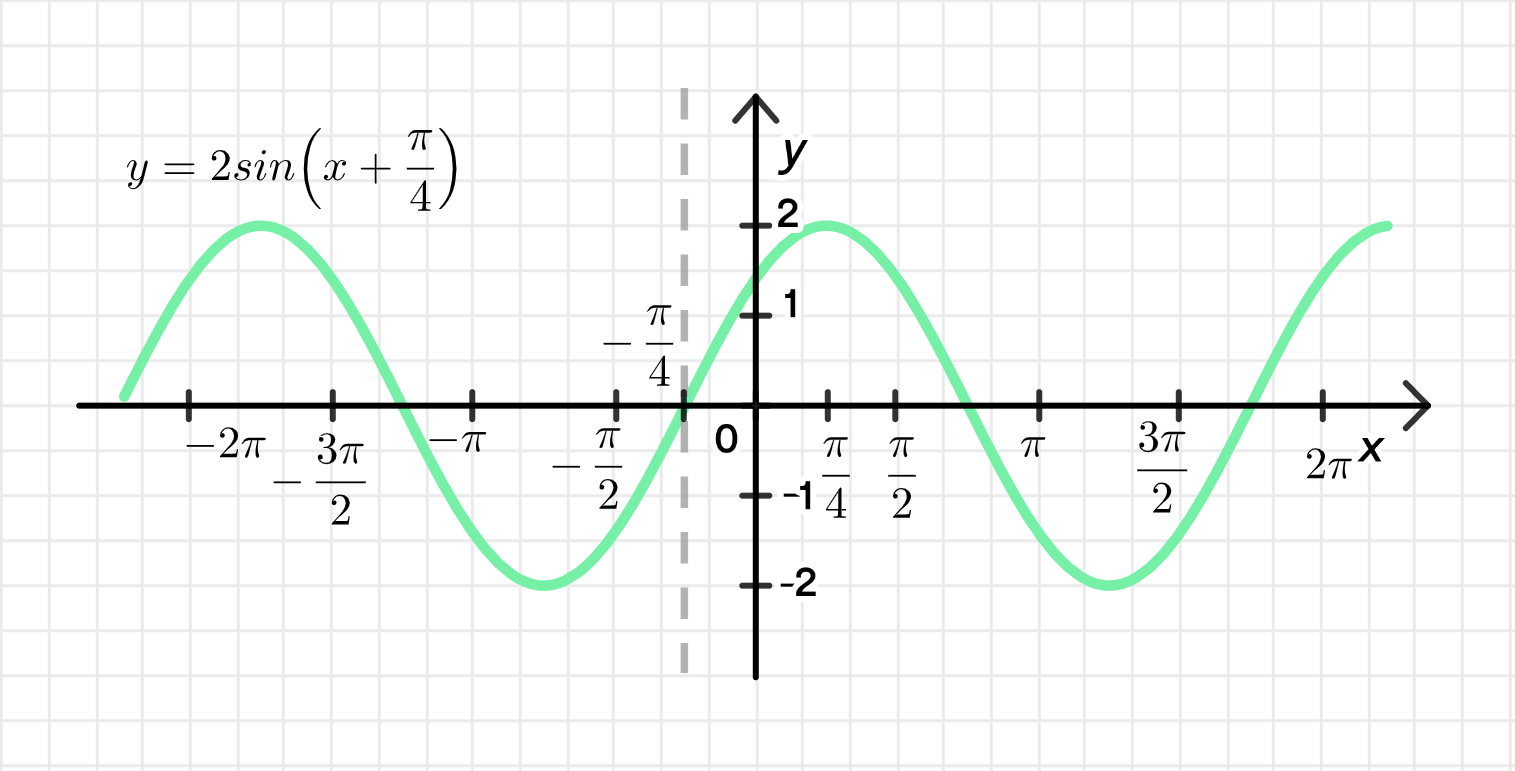
$$y=\sqrt{2}(\sin x+\cos x)$$

б)

$$y=\sqrt{3}\sin x+\cos x$$

в)

$$y=\sin x-\sqrt{3}\cos x$$

г)

$$y=\sin x-\cos x$$

а)

$$y = \sqrt{2} (\sin x + \cos x) = \sqrt{2} \cdot \sqrt{1+1} \sin \left( x + \arcsin \frac{1}{\sqrt{1+1}} \right);$$ $$y = \sqrt{2} \cdot \sqrt{2} \sin \left( x + \arcsin \frac{1}{\sqrt{2}} \right) = 2 \sin \left( x + \frac{\pi}{4} \right);$$

1) Построим одну дугу графика функции $y = \sin x$, а затем:

• Переместим ее на $\frac{\pi}{4}$ единиц влево вдоль оси абсцисс;
• Совершим ее растяжение от оси $Ox$ с коэффициентом $k = 2$;

2) Достроим график функции:

б)

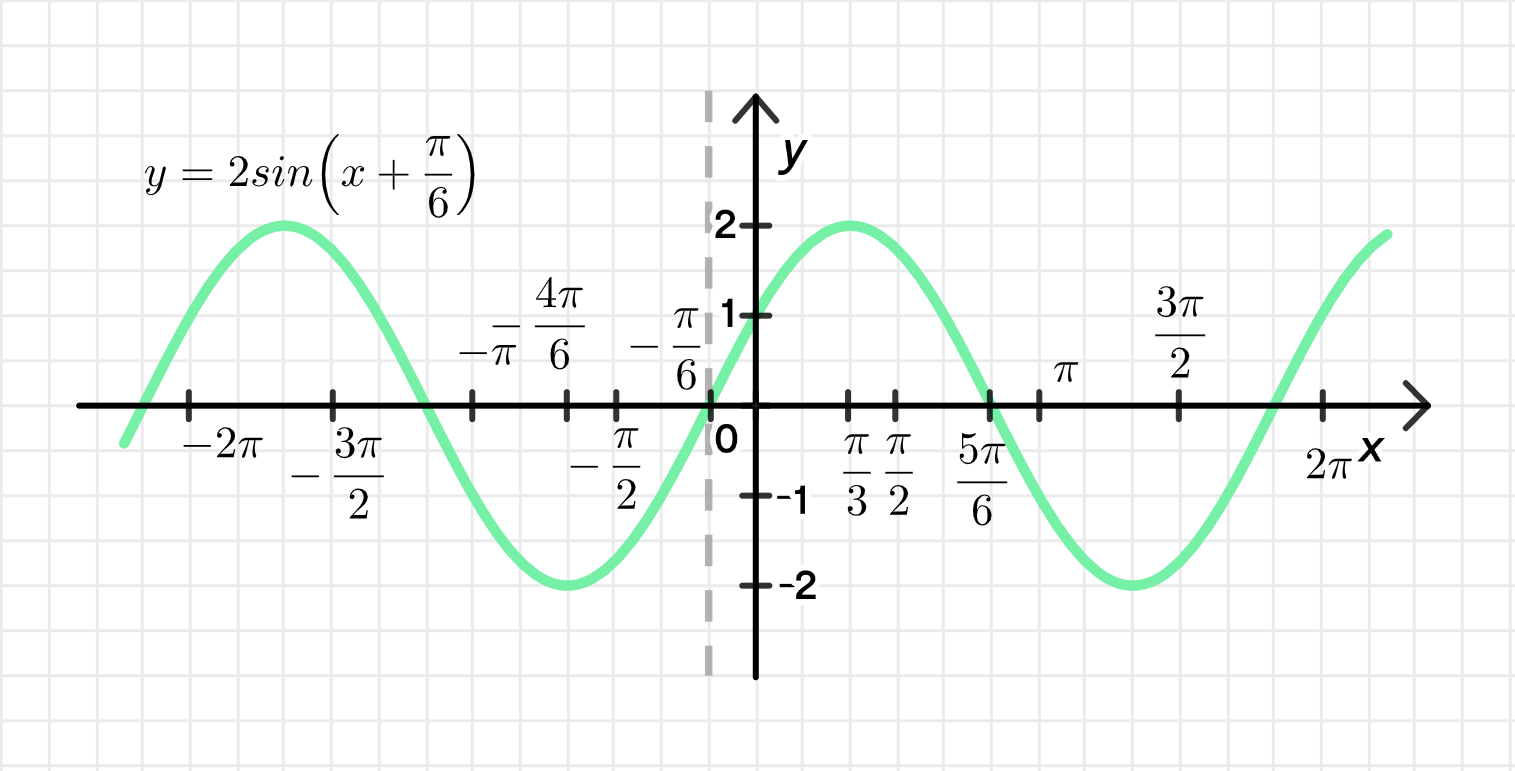
$$y = \sqrt{3} \sin x + \cos x = \sqrt{3+1} \sin \left( x + \arcsin \frac{1}{\sqrt{3+1}} \right);$$ $$y = 2 \sin \left( x + \arcsin \frac{1}{2} \right) = 2 \sin \left( x + \frac{\pi}{6} \right);$$

1) Построим одну дугу графика функции $y = \sin x$, а затем:

• Переместим ее на $\frac{\pi}{6}$ единиц влево вдоль оси абсцисс;
• Совершим ее растяжение от оси $Ox$ с коэффициентом $k = 2$;

2) Достроим график функции:

в)

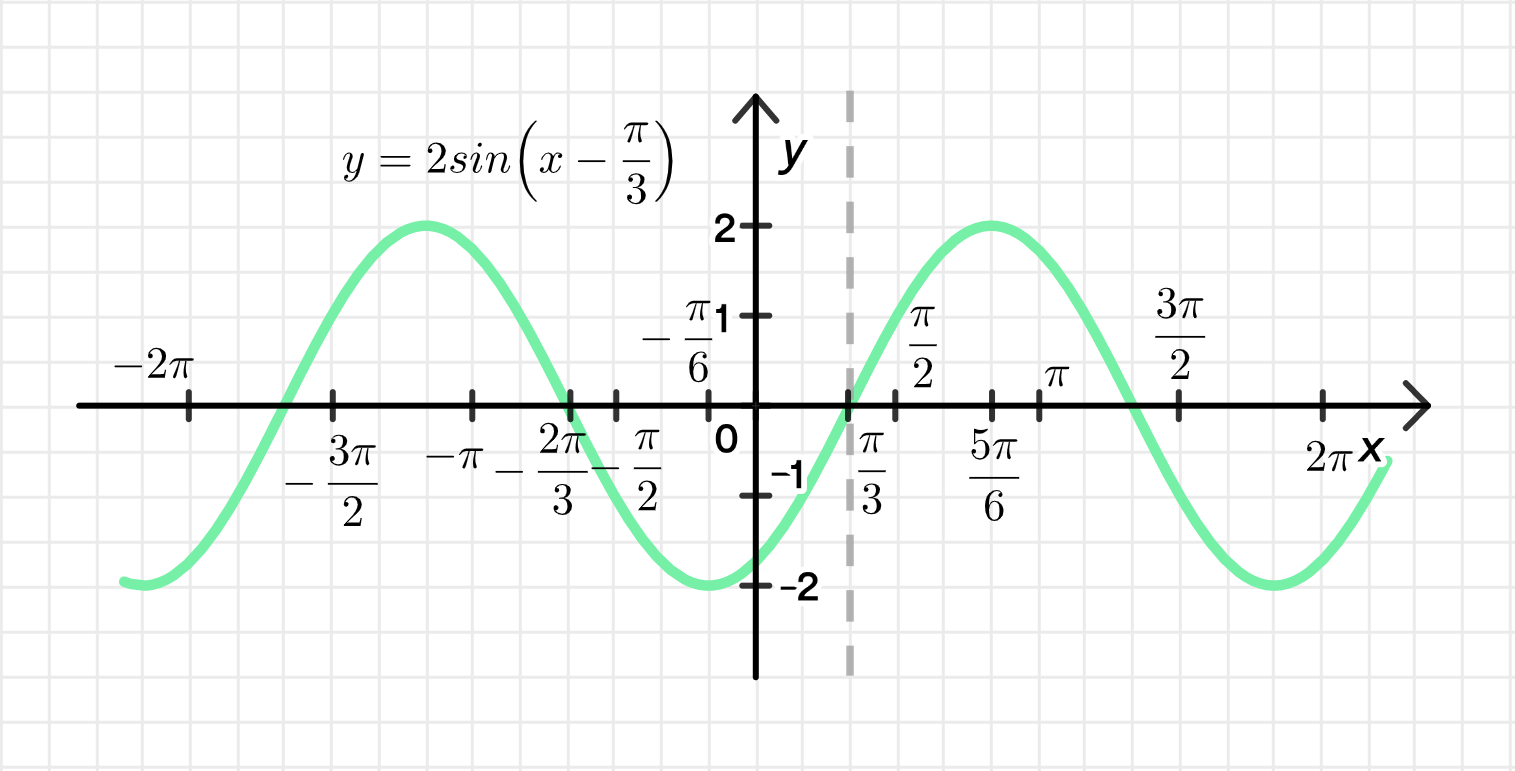
$$y = \sin x — \sqrt{3} \cos x = \sqrt{1+3} \sin \left( x — \arccos \frac{1}{\sqrt{1+3}} \right);$$ $$y = 2 \sin \left( x — \arccos \frac{1}{2} \right) = 2 \sin \left( x — \frac{\pi}{3} \right);$$

1) Построим одну дугу графика функции $y = \sin x$, а затем:

• Переместим ее на $\frac{\pi}{3}$ единиц вправо вдоль оси абсцисс;
• Совершим ее растяжение от оси $Ox$ с коэффициентом $k = 2$;

2) Достроим график функции:

г)

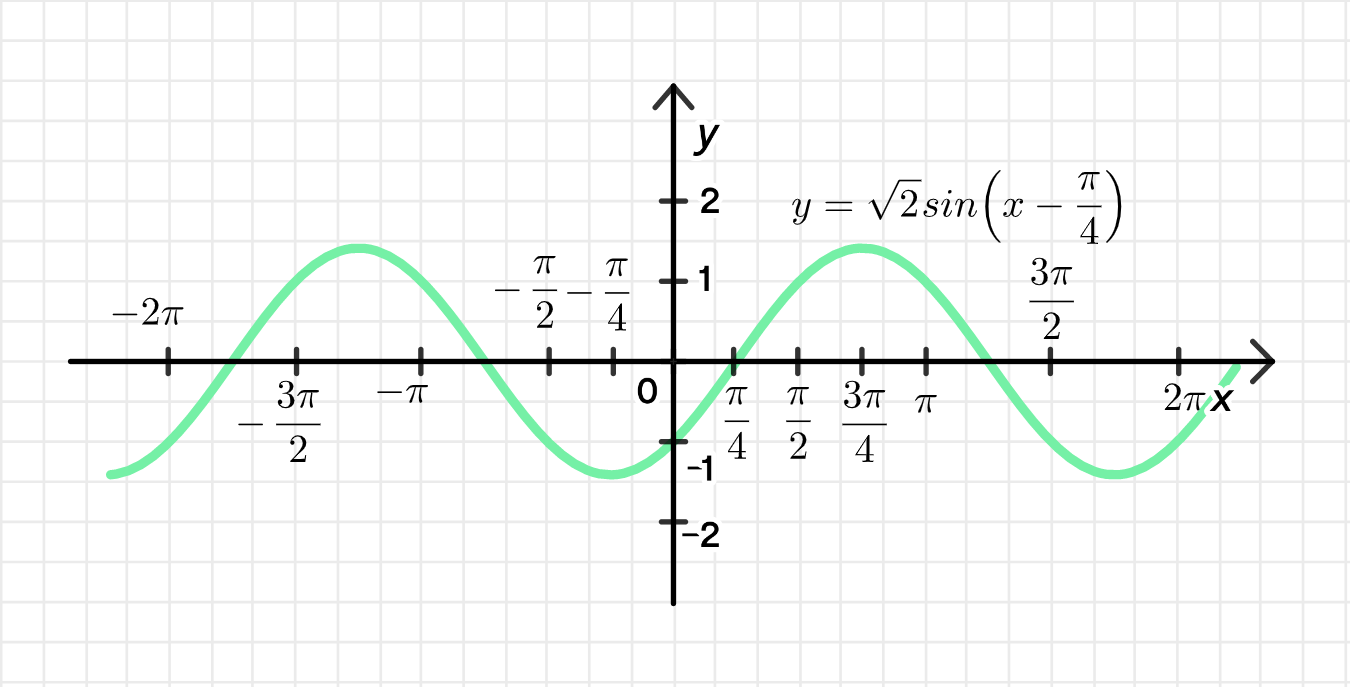
$$y = \sin x — \cos x = \sqrt{1+1} \sin \left( x — \arcsin \frac{1}{\sqrt{1+1}} \right);$$ $$y = \sqrt{2} \sin \left( x — \arcsin \frac{1}{\sqrt{2}} \right) = \sqrt{2} \sin \left( x — \frac{\pi}{4} \right);$$

1) Построим одну дугу графика функции $y = \sin x$, а затем:

• Переместим ее на $\frac{\pi}{4}$ единиц вправо вдоль оси абсцисс;
• Совершим ее растяжение от оси $Ox$ с коэффициентом $k = \sqrt{2}$;

2) Достроим график функции:

Мы рассматриваем функции вида:

$$y = a \sin x + b \cos x$$

Такую функцию всегда можно привести к виду:

$$y = R \sin(x + \varphi)$$

где:

$R = \sqrt{a^2 + b^2}$ — амплитуда функции;

$\varphi$ — фазовый сдвиг, определяется из соотношений:

$$\cos \varphi = \frac{a}{R}, \quad \sin \varphi = \frac{b}{R}$$

или наоборот (если менять знак, зависит от того, хотим ли синус или косинус).

Теперь разберем все пункты по порядку:

а)

$$y = \sqrt{2} (\sin x + \cos x)$$

Шаг 1: Вынесем множитель $\sqrt{2}$

$$y = \sqrt{2} \sin x + \sqrt{2} \cos x$$

Шаг 2: Приведем к виду одного синуса

Здесь $a = \sqrt{2}, \quad b = \sqrt{2}$

Найдем амплитуду:

$$R = \sqrt{a^2 + b^2} = \sqrt{2 + 2} = \sqrt{4} = 2$$

Найдем угол $\varphi$:

$$\cos \varphi = \frac{a}{R} = \frac{\sqrt{2}}{2}, \quad \Rightarrow \varphi = \frac{\pi}{4}$$

Значит:

$$y = 2 \sin(x + \frac{\pi}{4})$$

Шаг 3: Построение графика

Построим график $y = \sin x$ на отрезке, например, от $-\pi$ до $\pi$.

Сдвиг на $\frac{\pi}{4}$ влево:

• Получаем график $y = \sin(x + \frac{\pi}{4})$
• Это означает, что каждый пик и впадина сдвигаются влево на $\frac{\pi}{4}$

Растяжение от оси $Ox$ в 2 раза:

• Увеличиваем амплитуду синуса с 1 до 2
• Значения функции теперь колеблются от –2 до 2

б)

$$y = \sqrt{3} \sin x + \cos x$$

Шаг 1: Приведем к виду одного синуса

Здесь $a = \sqrt{3}, \quad b = 1$

$$R = \sqrt{3 + 1} = \sqrt{4} = 2$$ $$\sin \varphi = \frac{1}{2} \Rightarrow \varphi = \frac{\pi}{6}$$

Значит:

$$y = 2 \sin(x + \frac{\pi}{6})$$

Шаг 2: Построение графика

Начнем с графика $y = \sin x$

Сдвигаем на $\frac{\pi}{6}$ влево → $y = \sin(x + \frac{\pi}{6})$

Умножаем на 2 (амплитуда становится равной 2)

в)

$$y = \sin x — \sqrt{3} \cos x$$

Шаг 1: Приведем к виду одного синуса

$a = 1, \quad b = -\sqrt{3}$

$$R = \sqrt{1^2 + (-\sqrt{3})^2} = \sqrt{1 + 3} = \sqrt{4} = 2$$ $$\cos \varphi = \frac{1}{2} \Rightarrow \varphi = \frac{\pi}{3}$$

Знак у $b$ отрицательный → фазовый сдвиг вправо

$$y = 2 \sin(x — \frac{\pi}{3})$$

Шаг 2: Построение графика

Начнем с $y = \sin x$

Сдвиг на $\frac{\pi}{3}$ вправо (из-за минуса)

Растяжение в 2 раза → амплитуда от –2 до 2

г)

$$y = \sin x — \cos x$$

Шаг 1: Приведем к виду одного синуса

$a = 1, \quad b = -1$

$$R = \sqrt{1 + 1} = \sqrt{2}$$ $$\cos \varphi = \frac{1}{\sqrt{2}} \Rightarrow \varphi = \frac{\pi}{4}$$

Знак у $b$ отрицательный → фазовый сдвиг вправо

$$y = \sqrt{2} \sin(x — \frac{\pi}{4})$$

Шаг 2: Построение графика

Построим $y = \sin x$

Сдвиг вправо на $\frac{\pi}{4}$

Увеличение амплитуды: максимум теперь $\sqrt{2} \approx 1{,}41$