ГДЗ по Алгебре 10 Класс Номер 33.1 Профильный Уровень Мордкович — Подробные Ответы

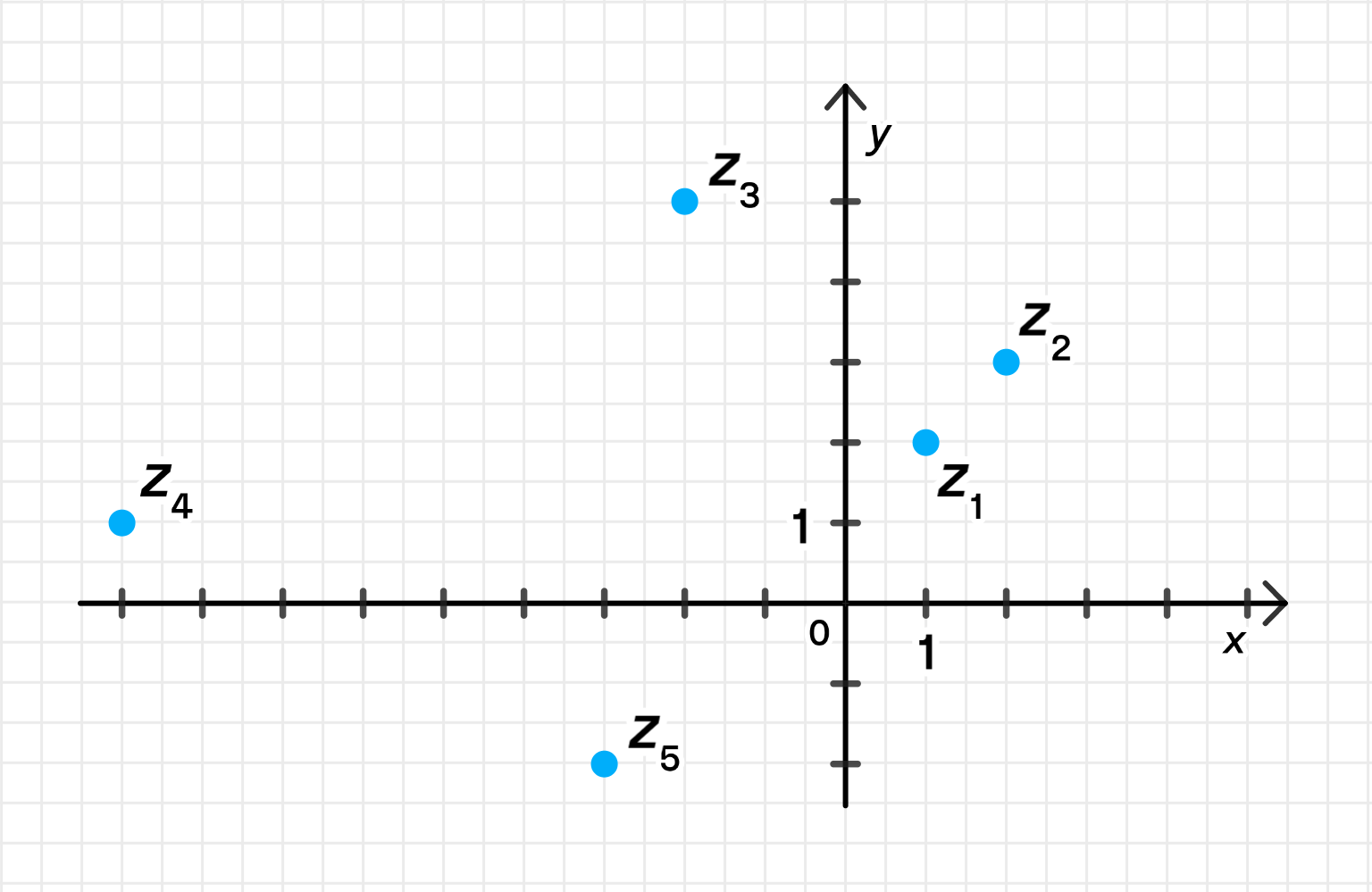
a) Отметьте на координатной плоскости точки, соответствующие комплексным числам

$$z_1=1+2i,z_2=2+3i,z_3=-2+5i,z_4=-9+i,z_5=-3-2\mathrm{i.}$$

б) Укажите те точки, которые лежат левее оси ординат. Что можно сказать о знаке действительной части каждой из таких точек?

в) Укажите те точки, которые лежат выше оси абсцисс. Что можно сказать о знаке мнимой части каждой из таких точек?

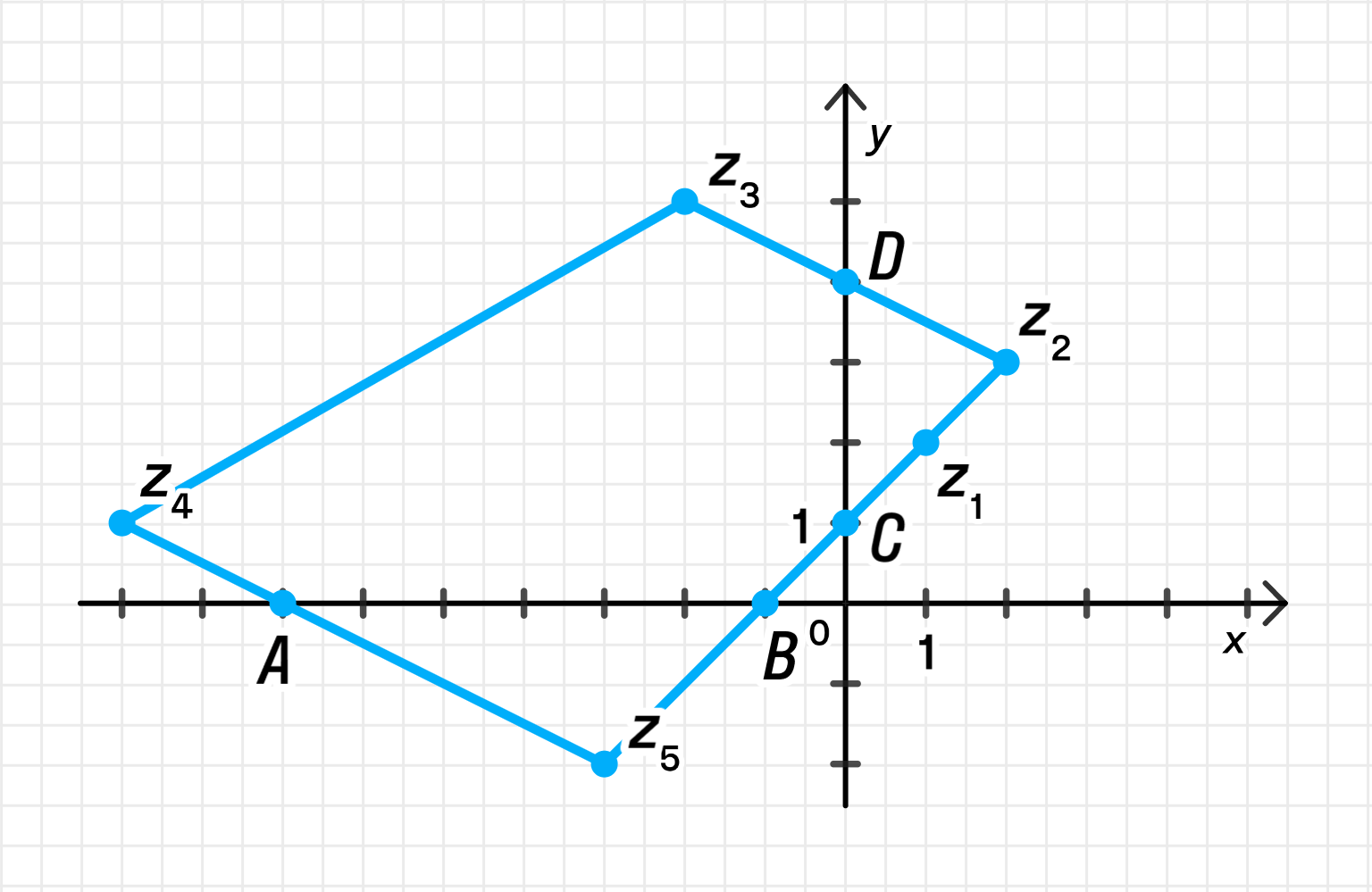
г) Соедините данные точки последовательно отрезками. Сколько получилось точек пересечения замкнутой ломаной с осями координат? Запишите комплексные числа, которым соответствуют эти точки.

Даны комплексные числа:

$$z_1=1+2i,z_2=2+3i,z_3=-2+5i,z_4=-9+i,z_5=-3-2i;$$

а) Данные точки на координатной плоскости:

б) Левее оси ординат лежат точки: $z_3,z_4,z_5$;
Действительная часть каждой такой точки отрицательна;

в) Выше оси абсцисс лежат точки: $z_1,z_2,z_3,z_4$;
Мнимая часть каждой такой точки положительна:

г) Соединим последовательно данные точки отрезками:

Замкнутая ломаная имеет 4 пересечения с осями координат:

$$z_6=0+4i=4i;$$$$z_7=-7+0i=-7;$$$$z_8=-1+0i=-1;$$$$z_9=0+1i=i$$

Дано:

Комплексные числа:

$$z_1=1+2i,z_2=2+3i,z_3=-2+5i,z_4=-9+i,z_5=-3-2i$$

Каждое комплексное число — это точка на комплексной плоскости (Аргана), где:

• $x=\text{Re}(z)$ — действительная часть (ось абсцисс);
• $y=\text{Im}(z)$ — мнимая часть (ось ординат).

а) Построение точек на координатной плоскости

Запишем координаты:

б) Определим, какие точки находятся левее оси ординат

Ось ординат — это прямая $x=0$.
Если $\text{Re}(z)<0$, точка лежит левее оси ординат.

Проверим каждую точку:

• $z_1=1+2i$: $x=1$ → не подходит
• $z_2=2+3i$: $x=2$ → не подходит
• $z_3=-2+5i$: $x=-2$
• $z_4=-9+i$: $x=-9$
• $z_5=-3-2i$: $x=-3$

Ответ:

$$\text{Левее оси ординат: }{z}_3,z_4,z_5$$

Признак: $\text{Re}(z)<0$

в) Определим, какие точки выше оси абсцисс

Ось абсцисс — это прямая $y=0$.
Если $\text{Im}(z)>0$, точка лежит выше оси абсцисс.

Проверим:

• $z_1=1+2i$: $y=2$
• $z_2=2+3i$: $y=3$
• $z_3=-2+5i$: $y=5$
• $z_4=-9+i$: $y=1$
• $z_5=-3-2i$: $y=-2$ → ✖️

Ответ:

$$\text{Выше оси абсцисс: }{z}_1,z_2,z_3,z_4$$

Признак: $\text{Im}(z)>0$

г) Построим замкнутую ломаную

Дано: соединить точки $z_1\to z_2\to z_3\to z_4\to z_5\to z_1$ — по порядку.

При построении такой ломаной, она может пересекать оси координат в некоторых точках.

Найдём точки пересечения ломаной с осями

Будем анализировать отрезки между парами точек и выяснять, какие отрезки пересекают ось $x=0$ (ординат) или $y=0$ (абсцисс).

Пересечения с осями координат

Из рисунка (предположительно — см. ссылку) указано:

• $z_6=0+4i=4i$ — пересечение с осью ординат;
• $z_7=-7+0i=-7$ — пересечение с осью абсцисс;
• $z_8=-1+0i=-1$ — пересечение с осью абсцисс;
• $z_9=0+1i=i$ — пересечение с осью ординат;

Проверим соответствие:

Итак, 4 пересечения:

• 2 на оси ординат: $z_6=4i$, $z_9=i$
• 2 на оси абсцисс: $z_7=-7$, $z_8=-1$

Ответ:

$$z_6=4i,z_7=-7,z_8=-1,z_9=i$$