ГДЗ по Алгебре 10 Класс Номер 33.10 Профильный Уровень Мордкович — Подробные Ответы

a) Действительная часть больше мнимой части;

б) мнимая часть не меньше действительной части;

в) мнимая часть больше 2, а действительная часть не больше 3;

г) мнимая часть не меньше 2, а действительная часть меньше 3.

Изобразить на координатной плоскости множество всех комплексных чисел $z$, у которых:

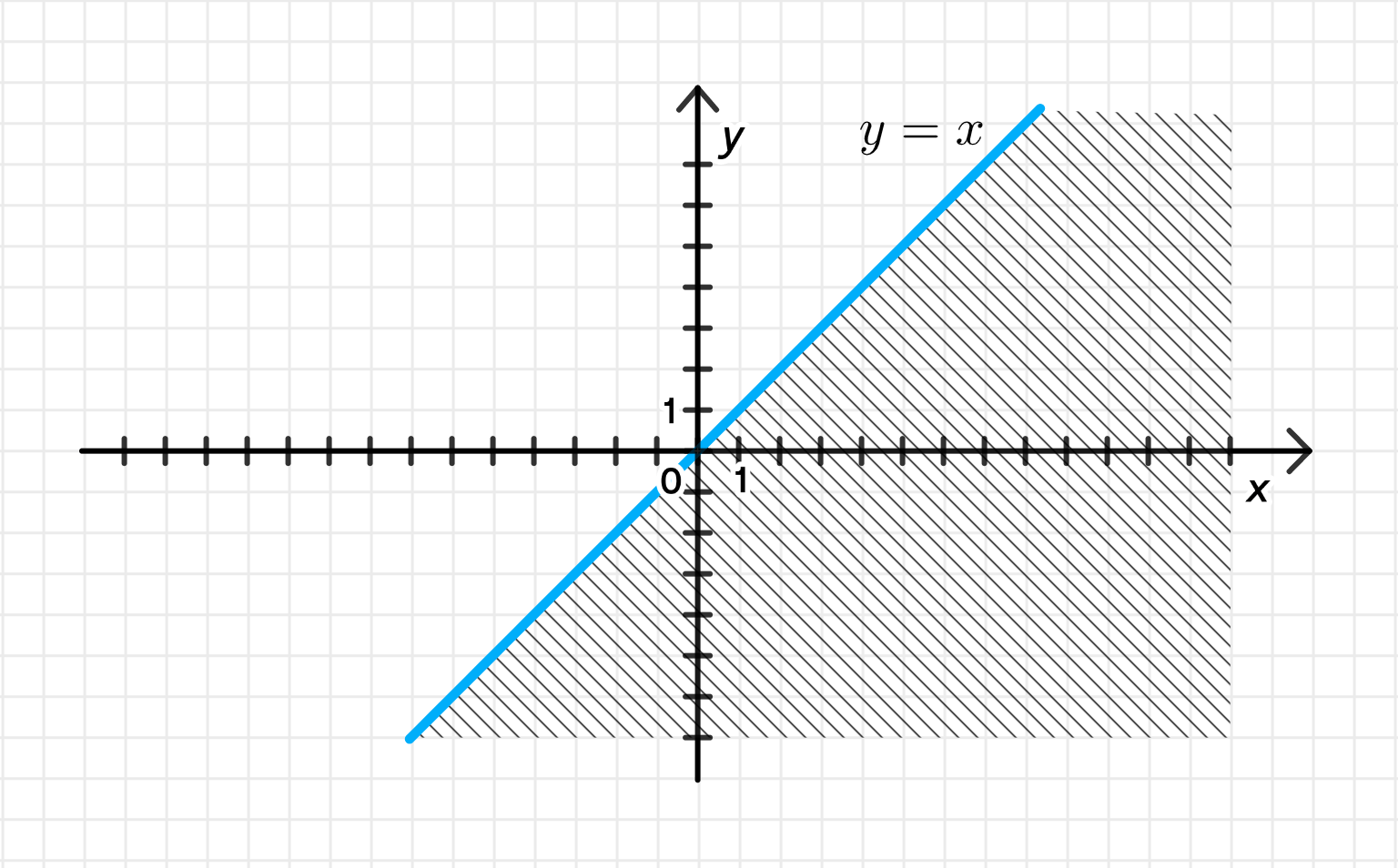
а) Действительная часть больше мнимой части:
$x>y;$

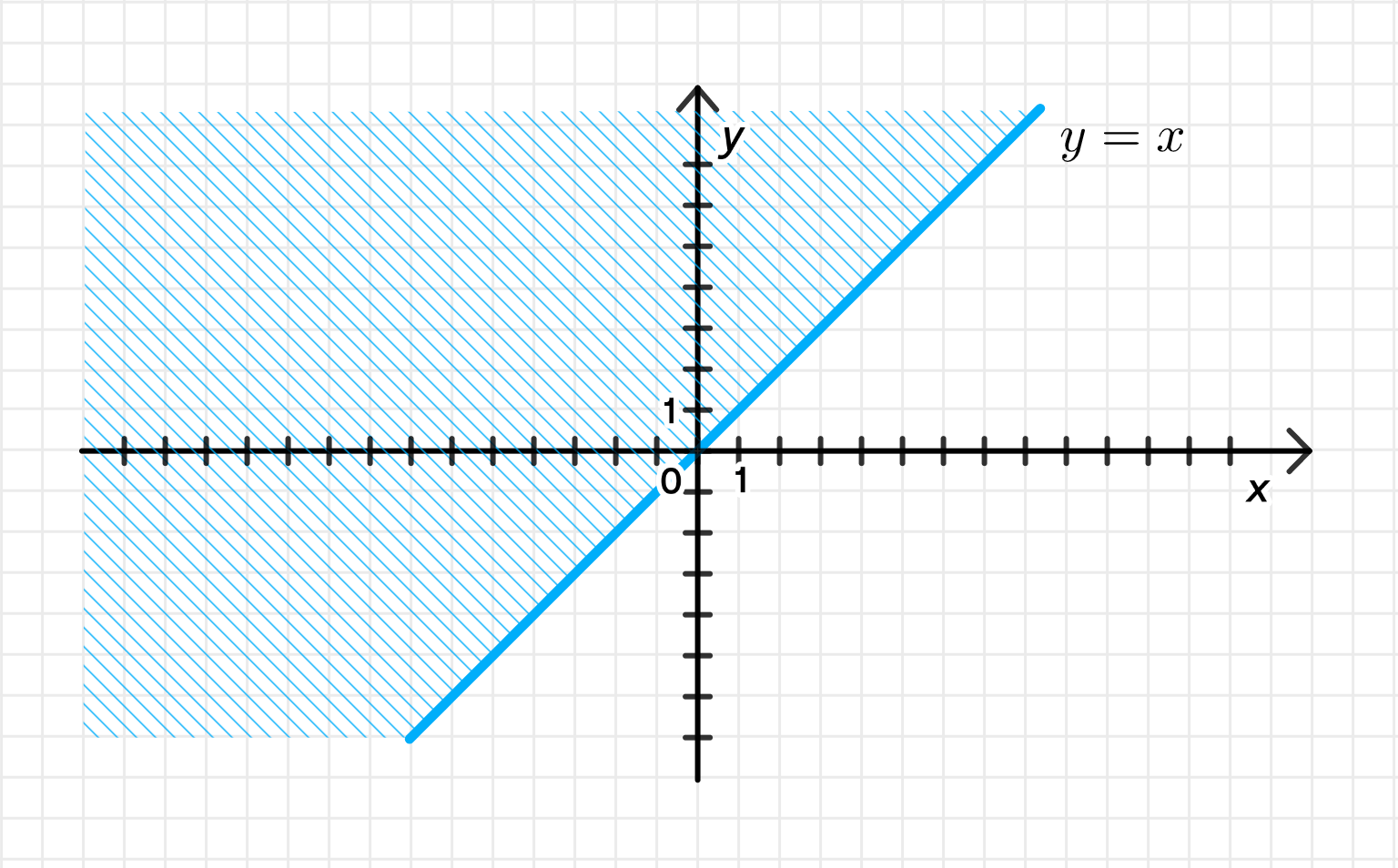
б) Мнимая часть не меньше действительной части:
$y\ge x;$

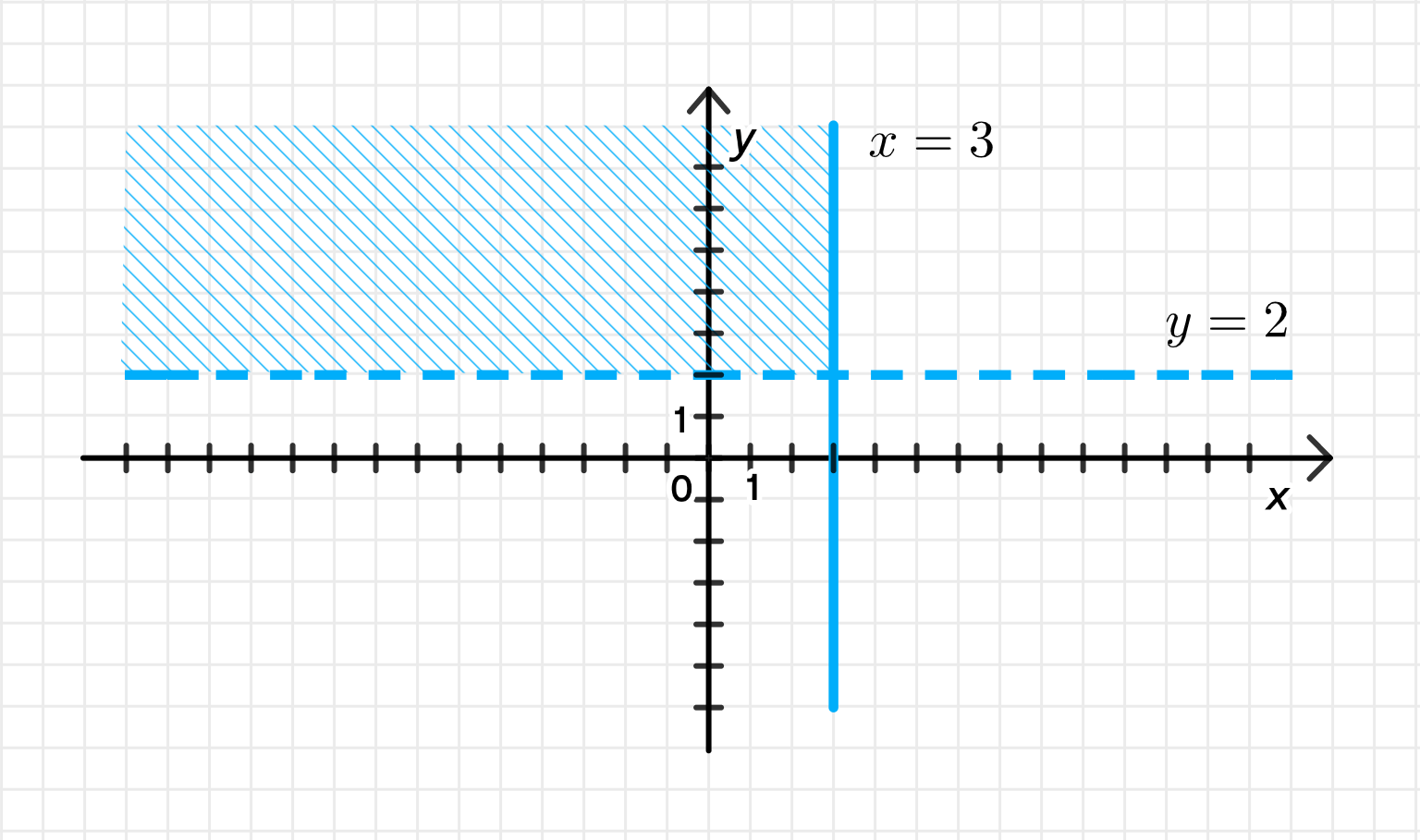
в) Мнимая часть больше 2, а действительная часть не больше 3:
$y>2\text{ и }x\le 3;$

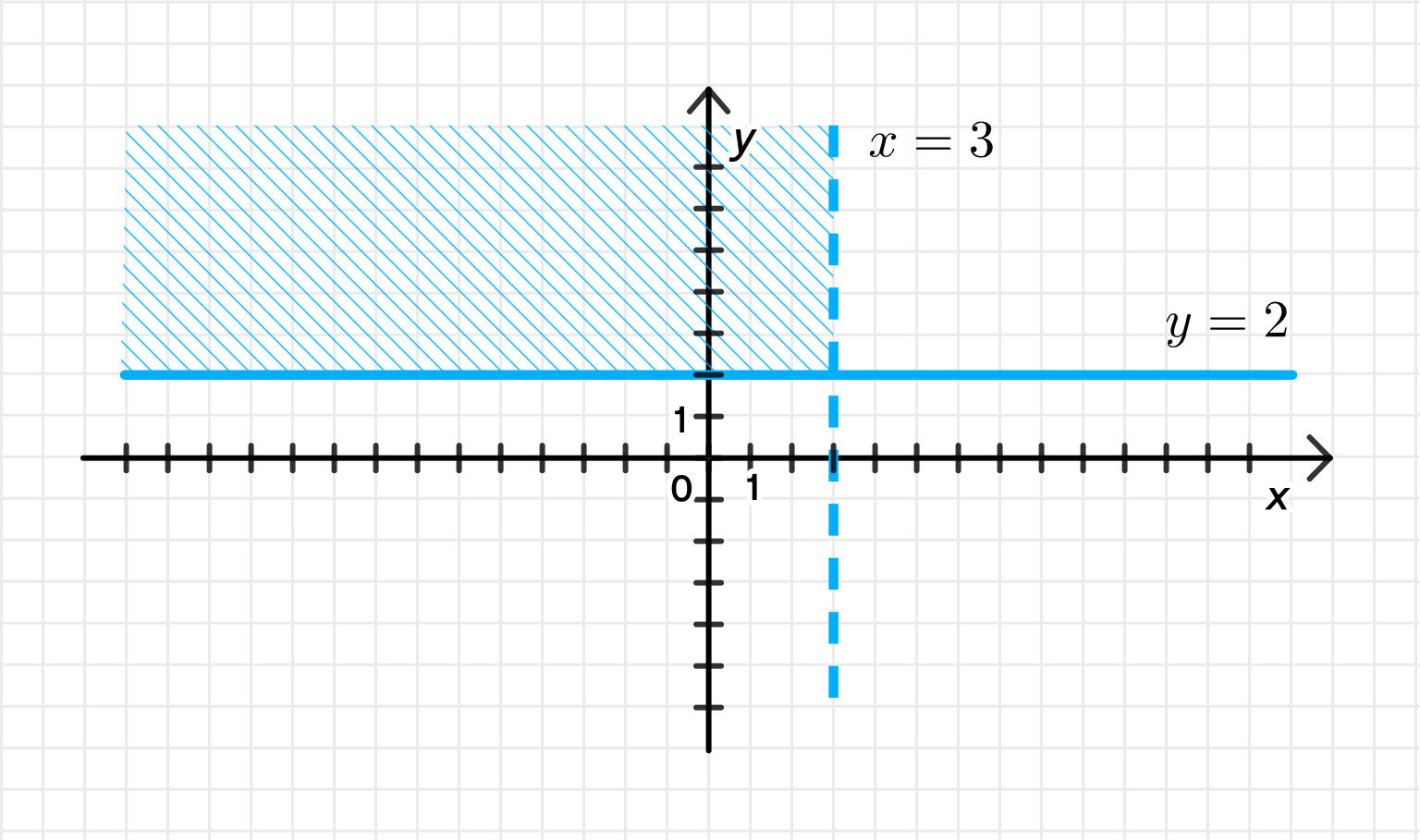
г) Мнимая часть не меньше 2, а действительная часть меньше 3:
$y\ge 2\text{ и }x<3;$

Общая информация:

Любое комплексное число $z$ можно записать в виде:

$$z=x+iy,$$

где:

• $x=\text{Re}(z)$ — действительная часть,
• $y=\text{Im}(z)$ — мнимая часть.

Чтобы изобразить множество таких чисел на координатной плоскости, мы будем рассматривать координатную плоскость $\mathbb{C}$ как обычную декартову плоскость с осями:

• ось абсцисс (горизонтальная) — действительная часть ($x$),
• ось ординат (вертикальная) — мнимая часть ($y$).

а) $x>y$

Условие:
Действительная часть больше мнимой части.

Переписываем:
Это означает, что каждая точка $(x,y)$ удовлетворяет неравенству:

$$x>y\mathrm{.}$$

Геометрический смысл:

• Прямая $x=y$ делит плоскость на две части.
• Все точки над этой прямой: $x<y$,
• Все точки под этой прямой: $x>y$.

Множество решений:
Полуплоскость ниже (не включая) прямой $x=y$.

Графически:

• Провести пунктирную прямую $x=y$ (пунктир, потому что неравенство строгое, без знака равенства),
• Зафштриховать область ниже этой прямой.

б) $y\ge x$

Условие:
Мнимая часть не меньше действительной части.

Переписываем:

$$y\ge x\mathrm{.}$$

Геометрический смысл:

• Это всё то, что находится на или выше прямой $y=x$.

Множество решений:
Полуплоскость, включая прямую $y=x$, лежащая выше неё.

Графически:

• Провести сплошную прямую $y=x$,
• Зафштриховать область над этой прямой (включая её).

в) $y>2$ и $x\le 3$

Условие:

• Мнимая часть больше 2,
• Действительная часть не больше 3.

Переписываем:

$$y>2\text{и}x\le 3.$$

Геометрический смысл:

• Прямая $y=2$ — горизонтальная. Всё выше этой прямой (не включая саму прямую) удовлетворяет $y>2$.
• Прямая $x=3$ — вертикальная. Всё слева или на этой прямой удовлетворяет $x\le 3$.

Множество решений:
Четверть-бесконечная область, ограниченная:

• снизу — прямой $y=2$ (не включается),
• справа — прямой $x=3$ (включается),
• не ограничена сверху и влево.

Графически:

• Провести пунктирную горизонтальную прямую $y=2$,
• Провести сплошную вертикальную прямую $x=3$,
• Зафштриховать область выше $y=2$ и слева от (или на) $x=3$.

г) $y\ge 2$ и $x<3$

Условие:

• Мнимая часть не меньше 2,
• Действительная часть меньше 3.

Переписываем:

$$y\ge 2\text{и}x<3.$$

Геометрический смысл:

• Прямая $y=2$: всё на или выше этой прямой.
• Прямая $x=3$: всё строго левее этой прямой.

Множество решений:
Область, ограниченная:

• снизу — прямой $y=2$ (включается),
• справа — прямой $x=3$ (не включается),
• не ограничена сверху и влево.

Графически:

• Провести сплошную горизонтальную прямую $y=2$,
• Провести пунктирную вертикальную прямую $x=3$,
• Зафштриховать область выше (или на) $y=2$ и левее $x=3$.