Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 33.11 Профильный Уровень Мордкович — Подробные Ответы
а) или ;
б) или ;
в) и ;
г) или
Изобразить на координатной плоскости множество всех комплексных чисел , у которых:
а) или ;
или ;
б) или ;
или ;
в) и ;
и ;
г) или ;
или ;
Каждое комплексное число можно отобразить как точку на плоскости, где:
- — горизонтальная ось (действительная часть),
- — вертикальная ось (мнимая часть).
Условные обозначения:
- — действительная часть (ось абсцисс),
- — мнимая часть (ось ординат).
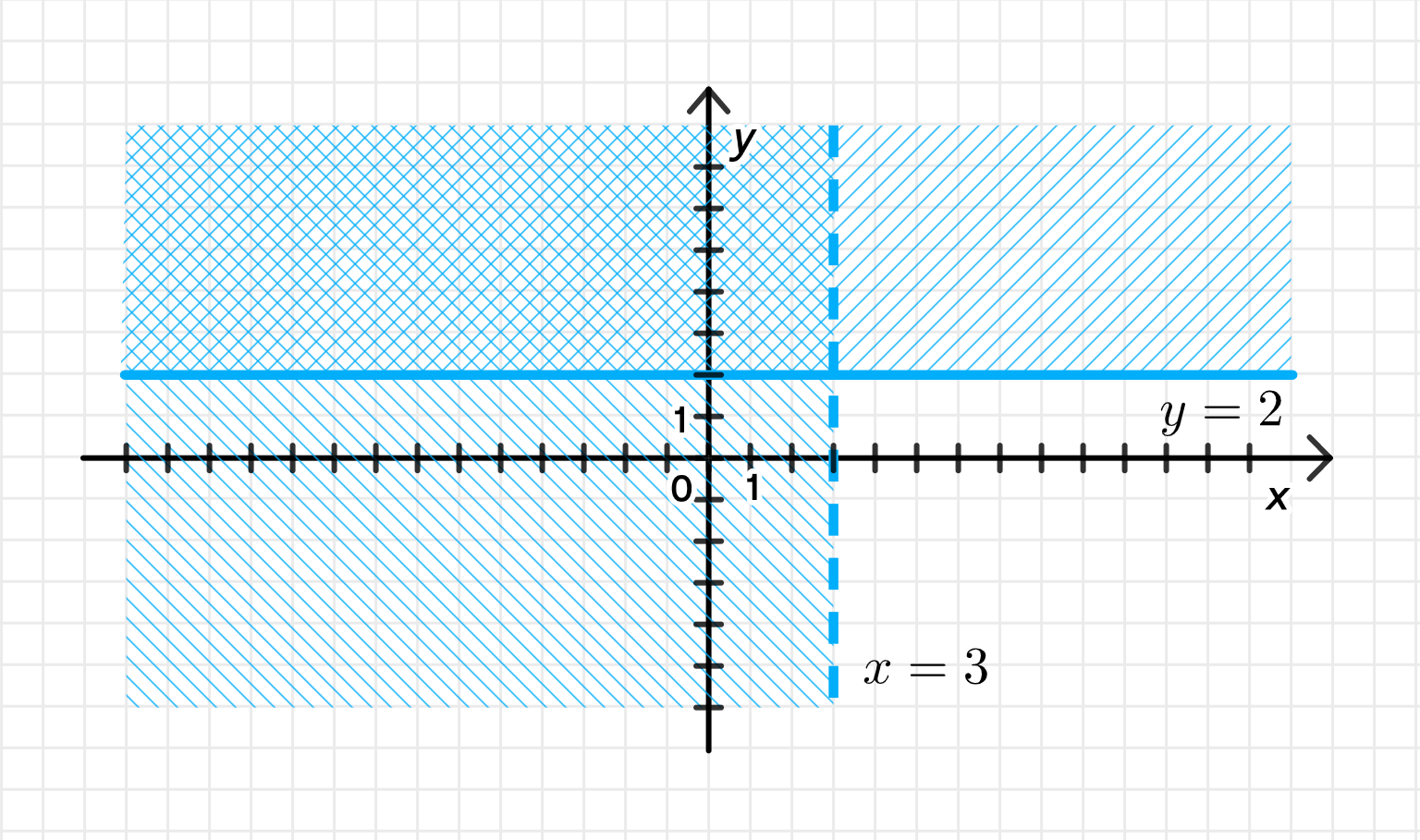
а) или
Интерпретация:
Это объединение двух областей:
- Все точки, у которых мнимая часть не меньше 2 — то есть выше (или на) прямой ,
- ИЛИ точки, у которых действительная часть строго меньше 3 — то есть левее прямой .
Геометрическая трактовка:
- Прямая — горизонтальная. Всё на ней и выше — подходит.
- Прямая — вертикальная. Всё строго левее неё — подходит.
- Поскольку это логическое ИЛИ, достаточно удовлетворения хотя бы одному из условий.
Итоговая область:
- Вся верхняя полуплоскость начиная с и выше (включительно),
- Вся левая часть плоскости левее (исключая саму прямую),
- Пересечение этих областей включается тоже (всё, что одновременно выше и левее ).
Графически:
- Нарисовать:
- Сплошную горизонтальную прямую ,
- Пунктирную вертикальную прямую ,
- Зафштриховать:
- Всё на и выше ,
- Всё левее ,
- Всё, что попадает в обе области тоже входит в решение.
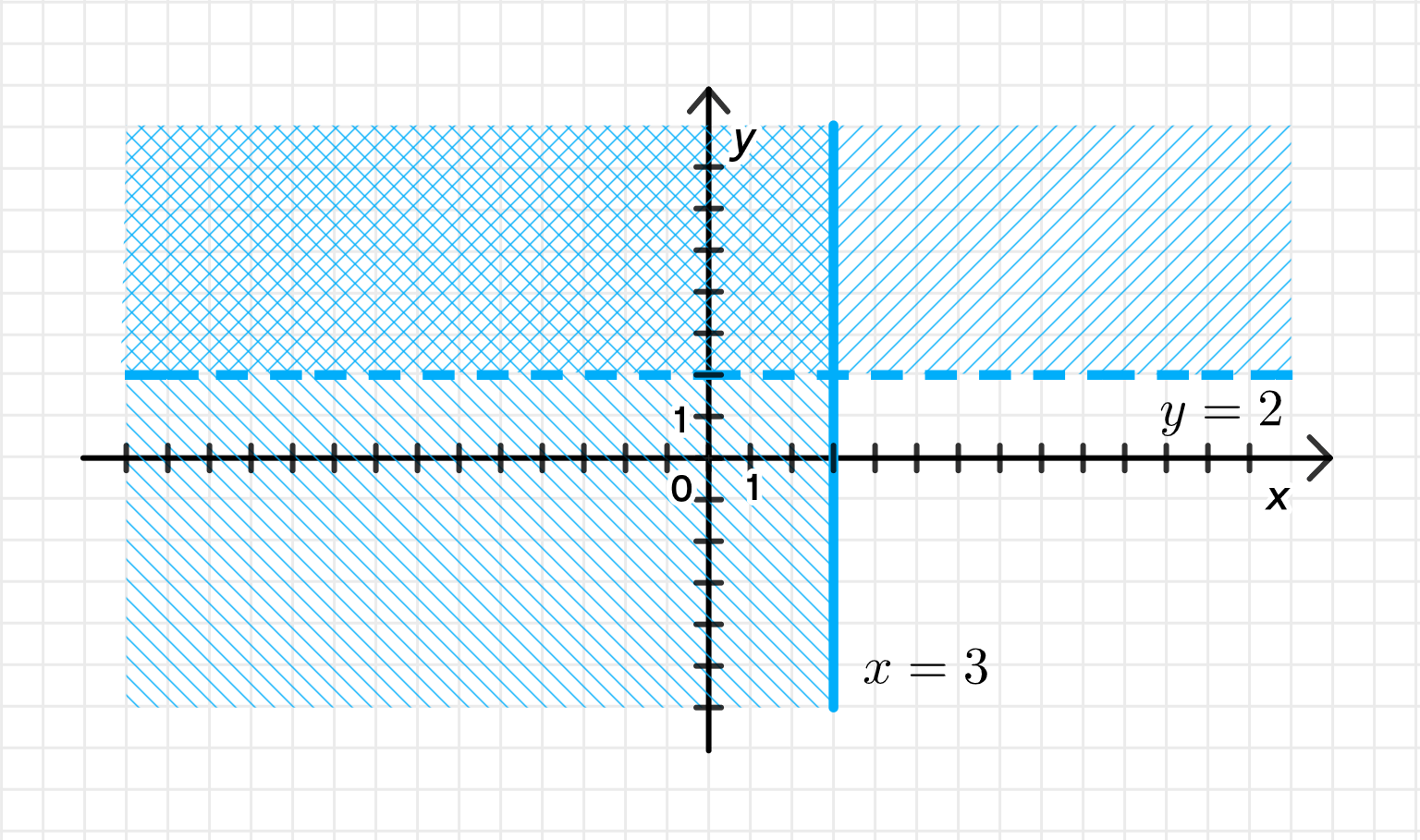
б) или
Интерпретация:
Также объединение двух условий:
- : строго выше горизонтальной прямой ,
- : на или левее вертикальной прямой .
Геометрическая трактовка:
- Горизонтальная прямая , пунктир: всё выше неё включается.
- Вертикальная прямая , сплошная: всё на и левее неё включается.
Итоговая область:
- Всё выше ,
- Всё на или левее ,
- Всё, что удовлетворяет хотя бы одному условию.
Графически:
- Провести:
- Пунктирную прямую ,
- Сплошную прямую ,
- Зафштриховать:
- Область выше ,
- Область на/левее ,
- Пересечение тоже входит.
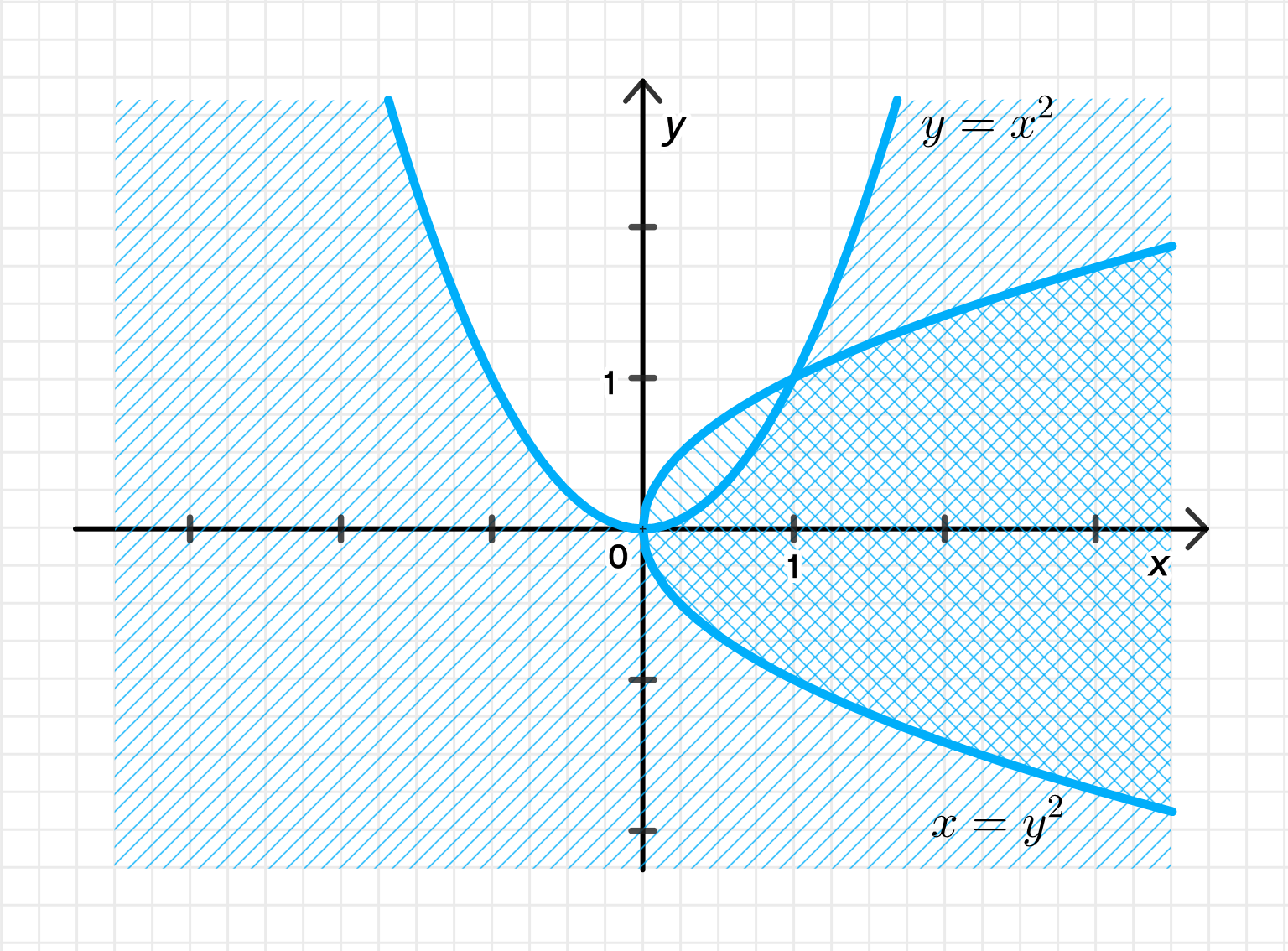
в) и
Интерпретация:
Теперь — логическое И (в отличие от предыдущих).
Необходимо, чтобы одновременно выполнялись:
- : то есть точка лежит правее параболы ,
- : то есть точка лежит ниже параболы .
Геометрическая трактовка:
- : парабола, ветви направлены вправо. Область правее неё — допустима.
- : парабола, ветви вверх. Область ниже неё — допустима.
Итоговая область:
- Пересечение двух областей:
- Справа от ,
- Ниже .
Графически:
- Построить обе параболы:
- — ось симметрии горизонтальная, вершина в начале координат.
- — обычная вертикальная парабола.
- Зафштриховать область:
- Лежащую правее параболы ,
- И одновременно ниже параболы .
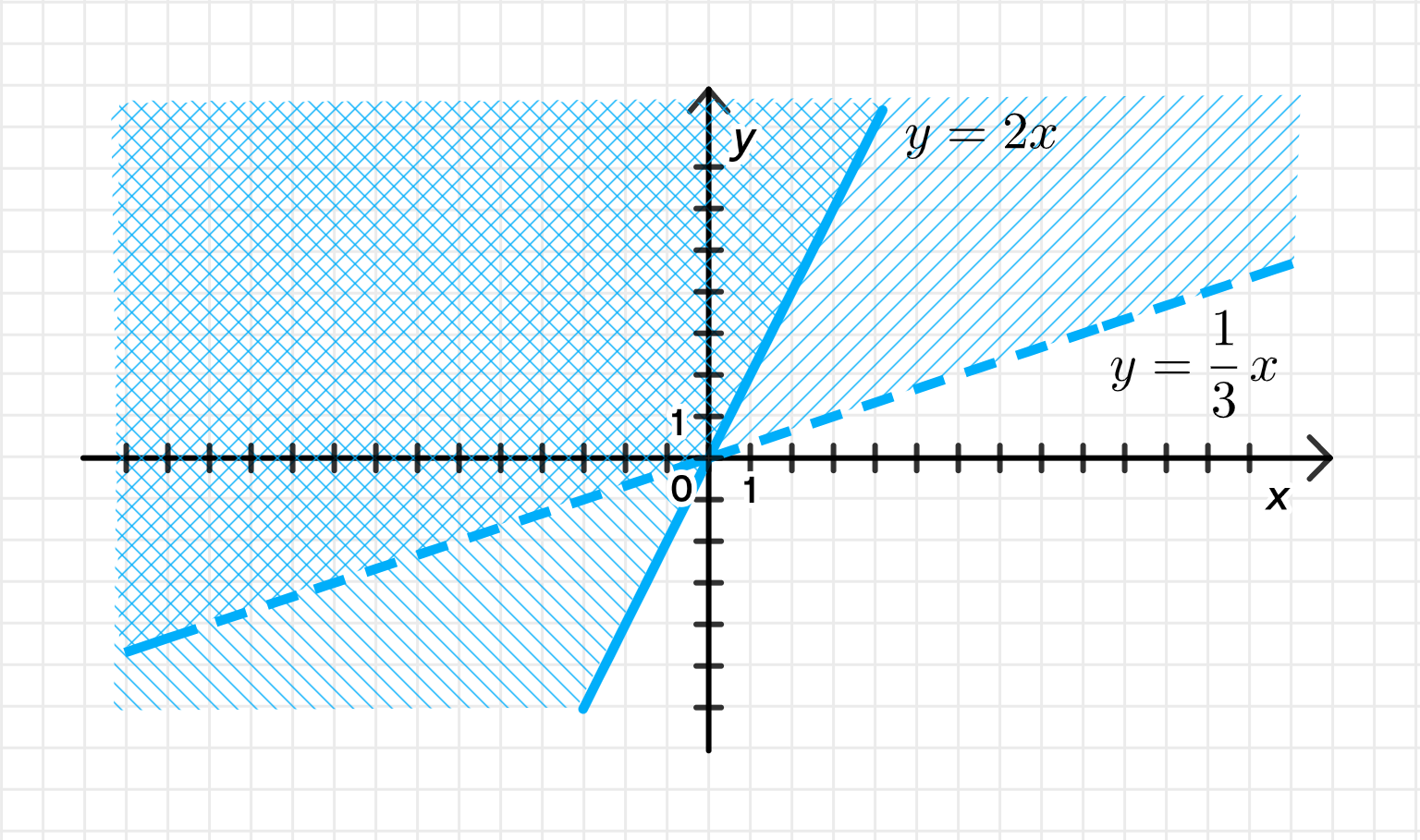
г) или
Интерпретация:
Объединение двух условий:
- : прямая с наклоном 2. Область выше или на ней.
- : прямая , область левее неё (не включая саму прямую).
Геометрическая трактовка:
- : наклонная прямая, угол 63°, проходит через 0. Область выше или на ней — допустима.
- : другая наклонная, угол ≈ 18°. Область строго левее — допустима.
Итоговая область:
- Всё, что:
- Лежит на/выше прямой ,
- ИЛИ лежит левее прямой ,
- ИЛИ удовлетворяет обоим сразу — всё включается.
Графически:
- Построить:
- Сплошную прямую ,
- Пунктирную прямую ,
- Зафштриховать:
- Область на/выше ,
- Область левее ,
- Пересечения — тоже входят.