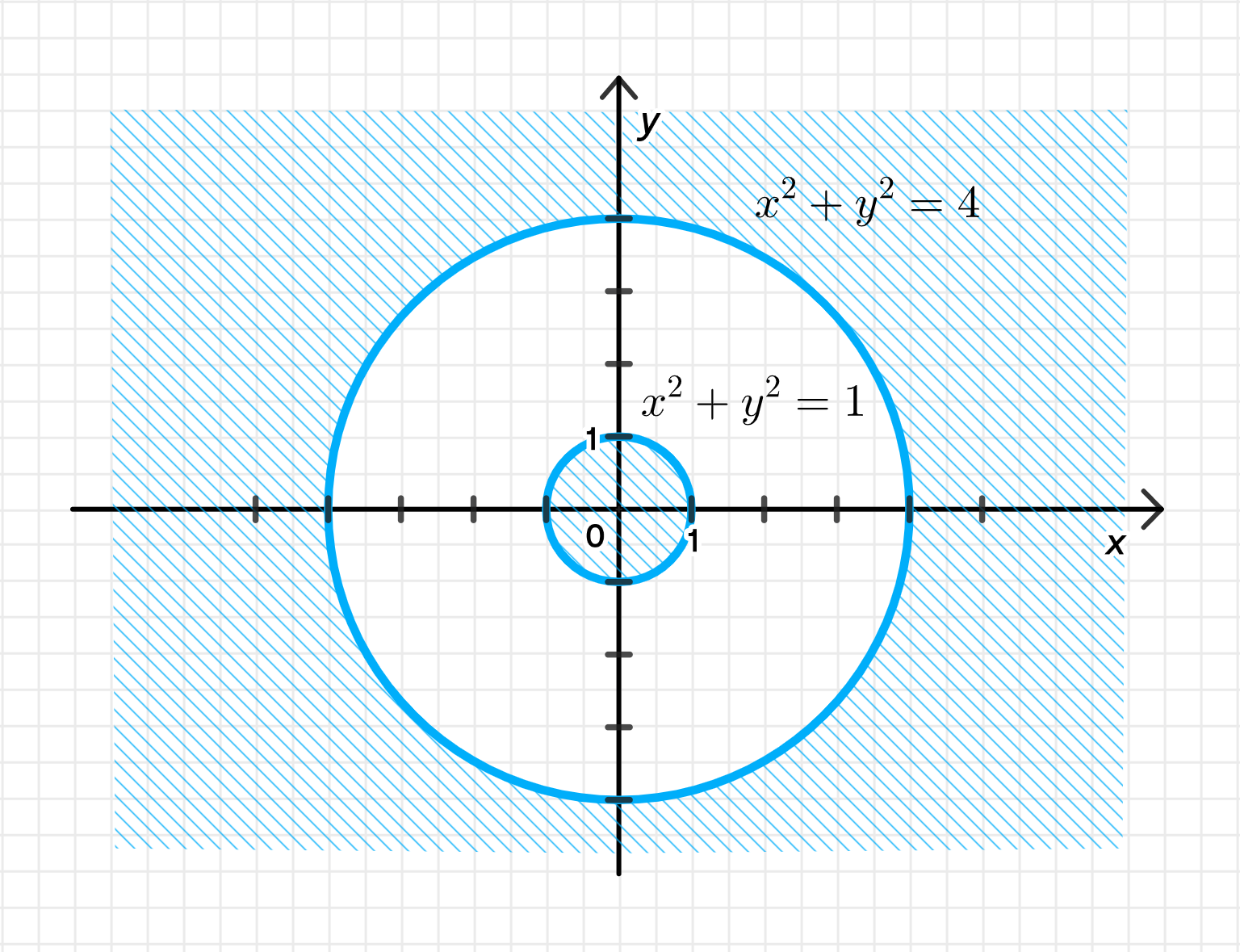ГДЗ по Алгебре 10 Класс Номер 33.12 Профильный Уровень Мордкович — Подробные Ответы

а) $Re\,z + Im\,z \geq 0$;

б) $1 < Re\,z + Im\,z < 2$;

в) $1 < (Re\,z)^2 + (Im\,z)^2 < 16$;

г) $(Re\,z)^2 + (Im\,z)^2 < 1$ или $16 < (Re\,z)^2 + (Im\,z)^2$

Изобразить на координатной плоскости множество всех комплексных чисел $z, y$, которых:

а) $Re\,z + Im\,z \geq 0$;
$x + y \geq 0$;
$y \geq -x$;

б) $1 < Re\,z + Im\,z < 2$;
$1 < x + y < 2$;
$x + y > 1$ и $x + y < 2$;
$y > 1 — x$ и $y < 2 — x$;

в) $1 < (Re\,z)^2 + (Im\,z)^2 < 16$;
$1 < x^2 + y^2 < 16$;
$x^2 + y^2 > 1$ и $x^2 + y^2 < 16$;

г) $(Re\,z)^2 + (Im\,z)^2 < 1$ или $16 < (Re\,z)^2 + (Im\,z)^2$;
$x^2 + y^2 < 1$ или $x^2 + y^2 > 16$;

Комплексное число $z$ можно представить в виде:

$$z = x + iy$$

где:

• $x = \text{Re}\,z$ — действительная часть,
• $y = \text{Im}\,z$ — мнимая часть.

Следовательно, каждое комплексное число можно рассматривать как точку $(x, y)$ на координатной плоскости (мнимая часть по вертикали, действительная — по горизонтали).

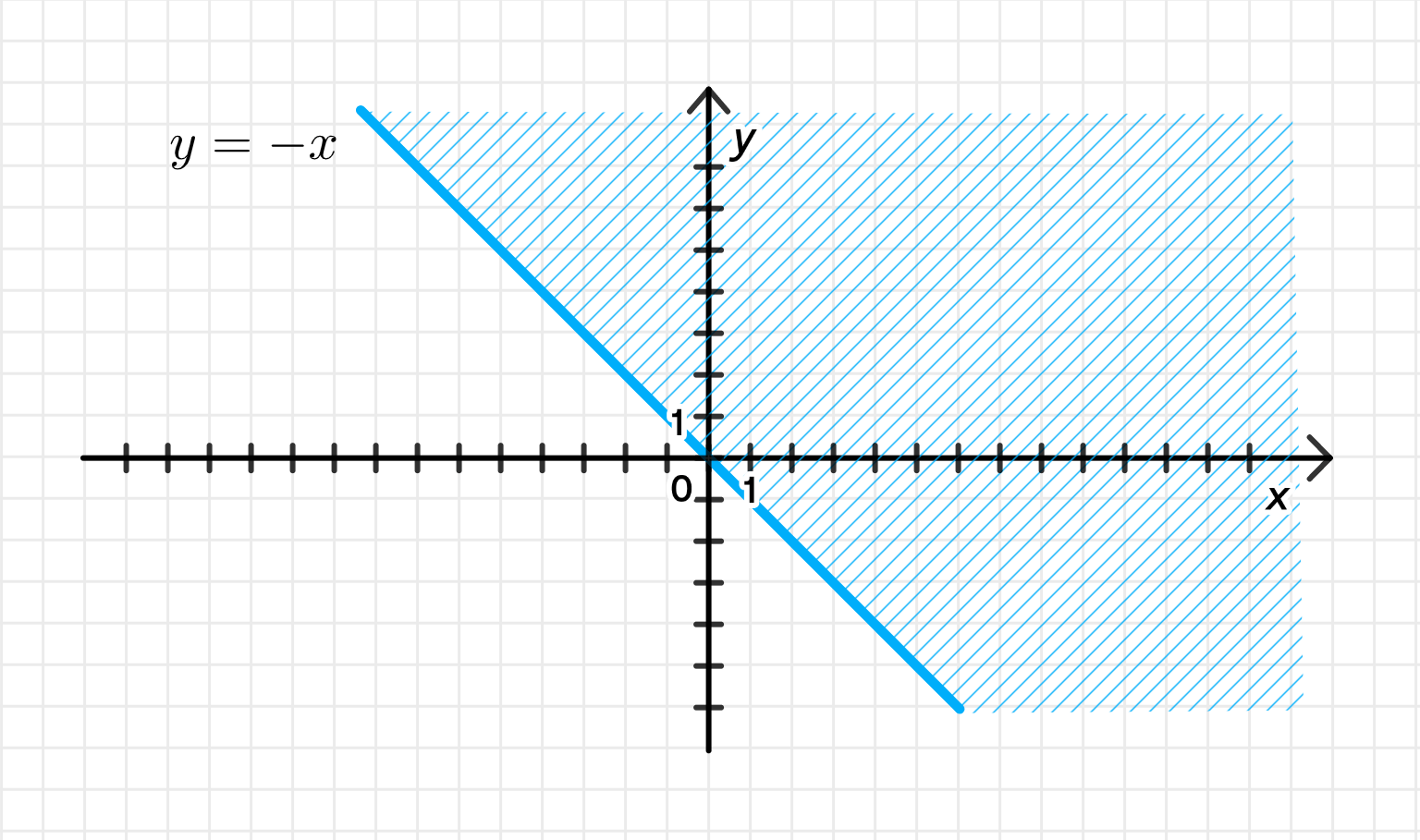
а) $\text{Re}\,z + \text{Im}\,z \geq 0$

Это:

$$x + y \geq 0 \quad \text{или} \quad y \geq -x$$

1. Определим границу:

Граница задается уравнением:

$$x + y = 0 \quad \Rightarrow \quad y = -x$$

Это прямая, проходящая через начало координат (точку (0,0)) под углом 45° к осям.

2. Область решения:

$$x + y \geq 0 \quad \Rightarrow \quad \text{все точки над (или на) прямой } y = -x$$

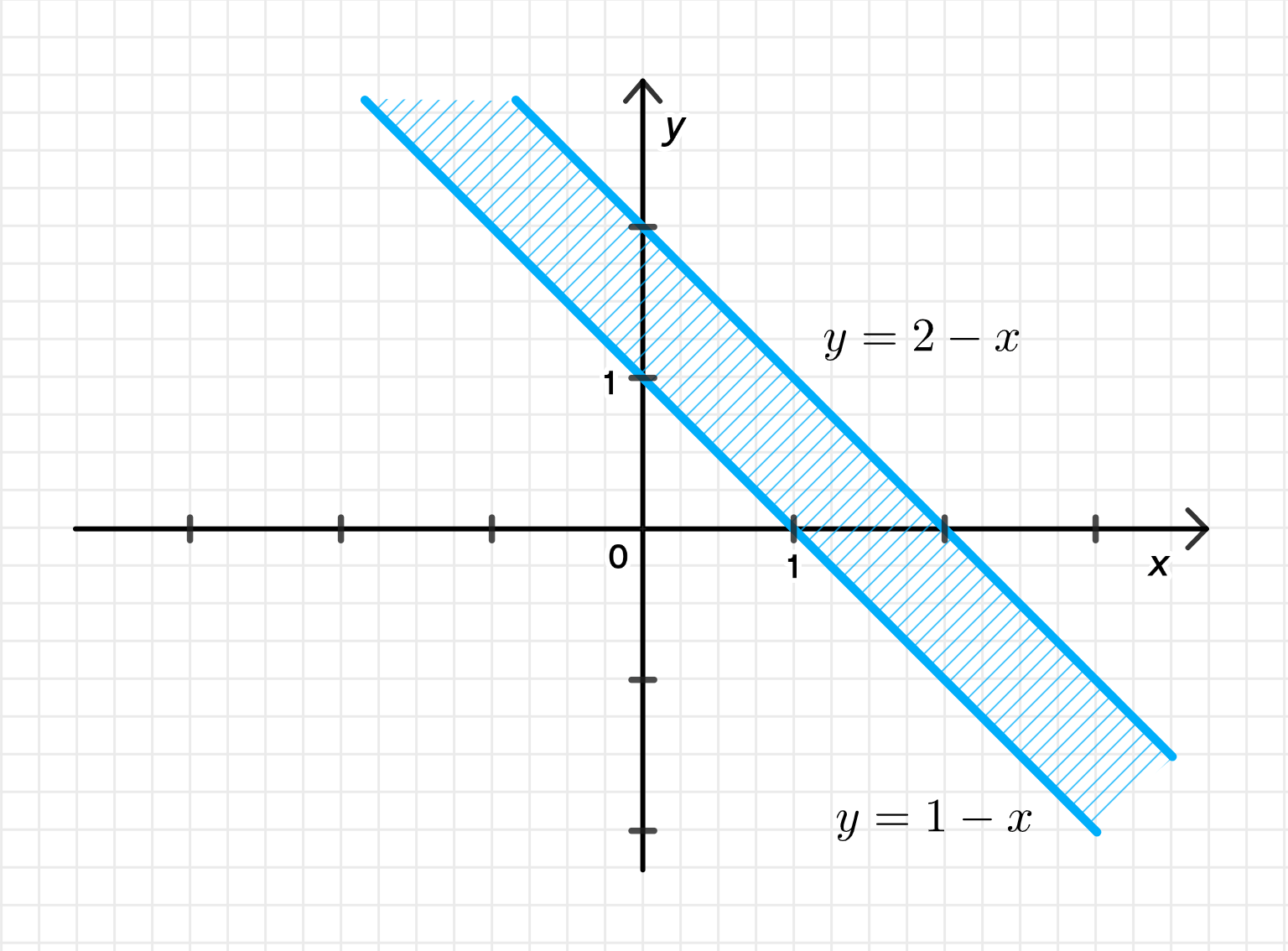
б) $1 < \text{Re}\,z + \text{Im}\,z < 2$

Это:

$$1 < x + y < 2 \quad \Rightarrow \quad \begin{cases} x + y > 1 \Rightarrow y > 1 — x \\ x + y < 2 \Rightarrow y < 2 — x \end{cases}$$

1. Определим границы:

• Первая граница — прямая $x + y = 1$ или $y = 1 — x$
• Вторая граница — прямая $x + y = 2$ или $y = 2 — x$

2. Область решения:

• Между этими прямыми.
• Исключаются точки на самих прямых, потому что знак строгий: $<$ и $>$, а не $\leq$ или $\geq$.

Это полоса, проходящая между двумя параллельными прямыми, наклоненными под 45°, шириной в 1 единицу по направлению, перпендикулярному оси $x = -y$.

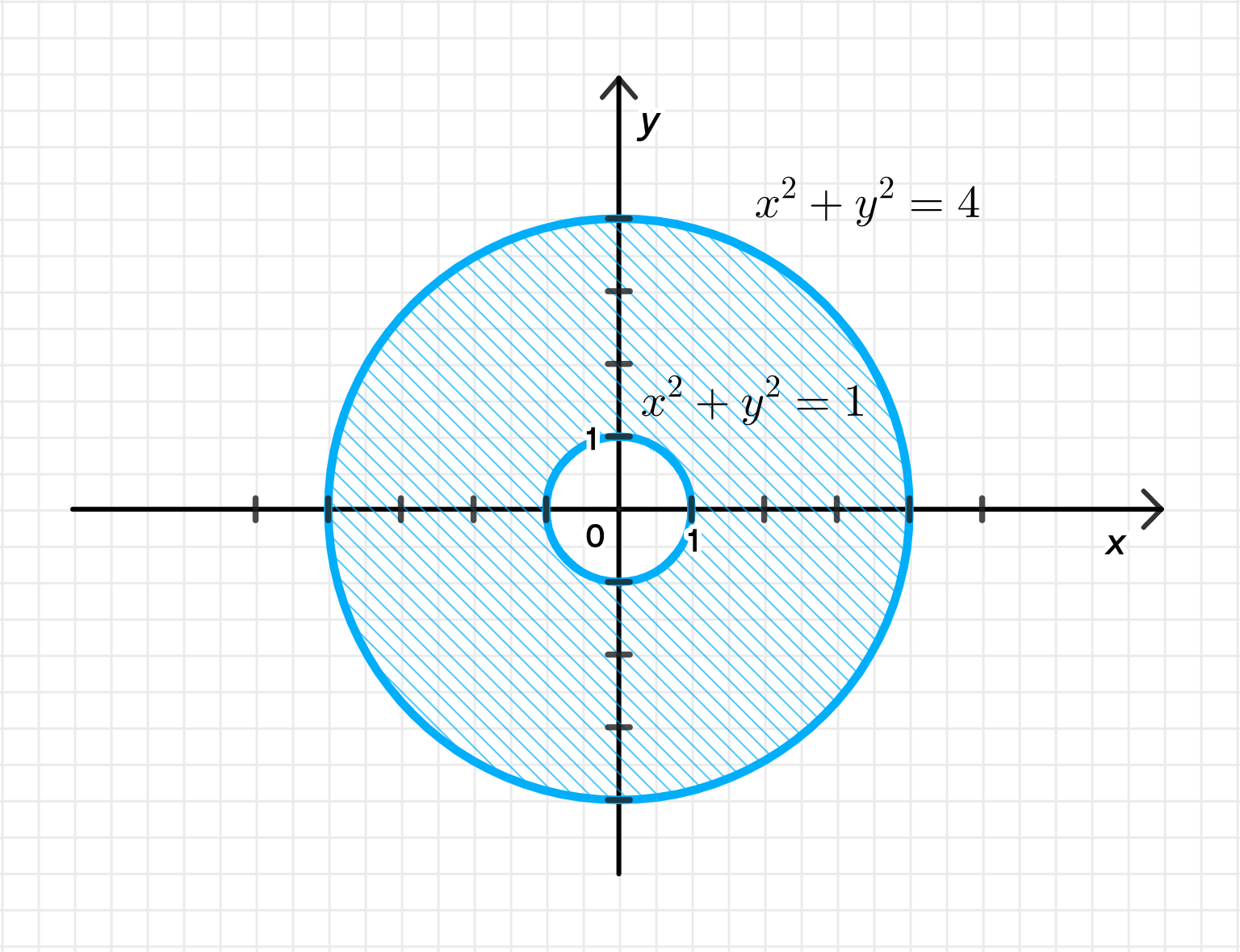
в) $1 < (\text{Re}\,z)^2 + (\text{Im}\,z)^2 < 16$

Это:

$$1 < x^2 + y^2 < 16$$

1. Распознаем геометрический смысл:

• $x^2 + y^2 = r^2$ — это уравнение окружности радиуса $r$, с центром в начале координат.
• В данном случае:
  • Внутренняя граница — круг радиуса $1$,
  • Внешняя граница — круг радиуса $4$ (так как $\sqrt{16} = 4$).

2. Область решения:

• Множество всех точек, находящихся в кольце между окружностями радиуса 1 и 4, исключая границы (строгие неравенства).

г) $(\text{Re}\,z)^2 + (\text{Im}\,z)^2 < 1$ или $16 < (\text{Re}\,z)^2 + (\text{Im}\,z)^2$

Это:

$$x^2 + y^2 < 1 \quad \text{или} \quad x^2 + y^2 > 16$$

1. Распознаем фигуры:

• Первая часть — внутри круга радиуса 1, исключая границу.
• Вторая часть — вне круга радиуса 4, также без границы.

2. Область решения:

• Это две несвязанные области:
  1. Круг радиуса 1 в центре (без границы);
  2. Все точки, находящиеся вне круга радиуса 4 (без границы).