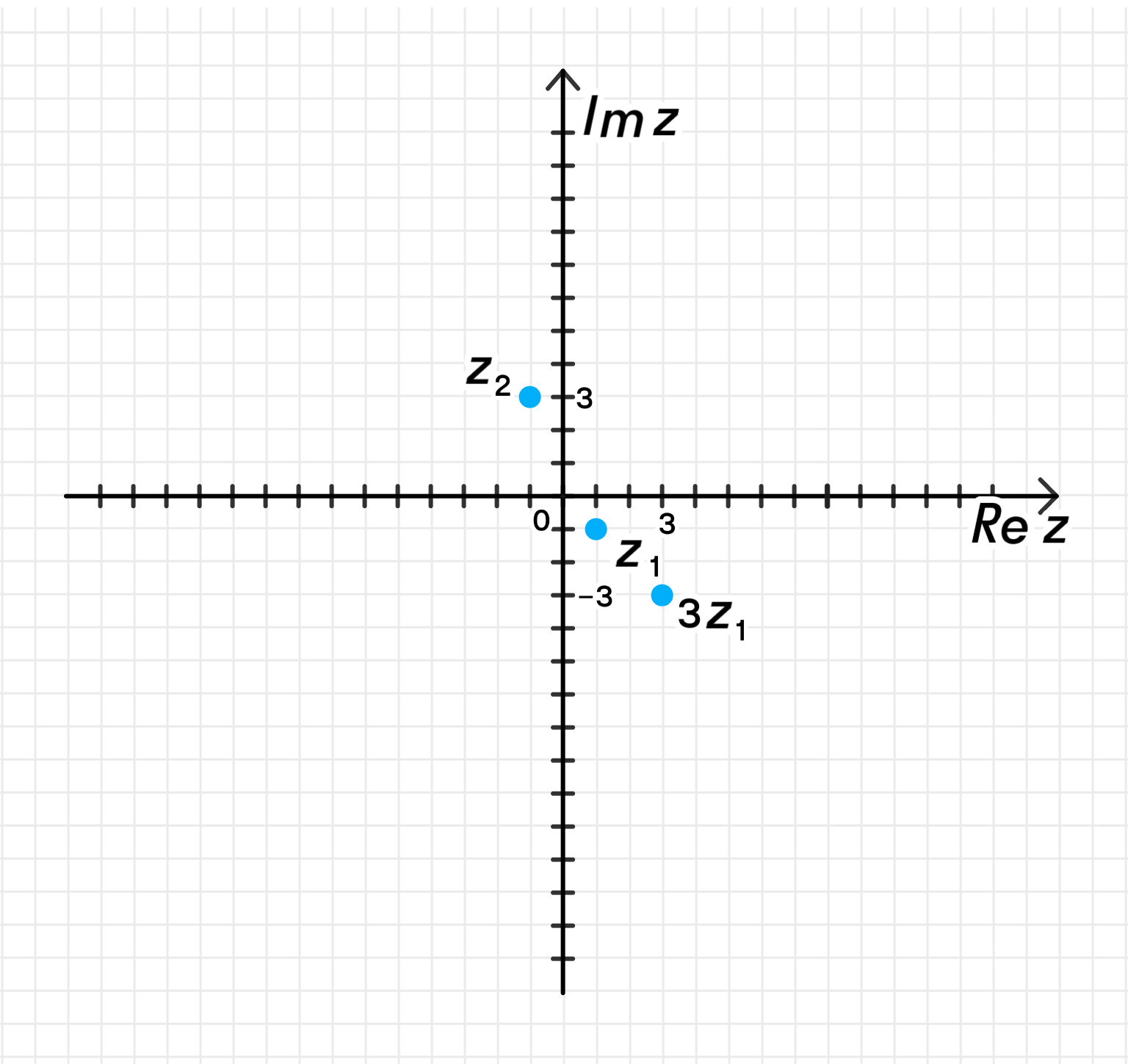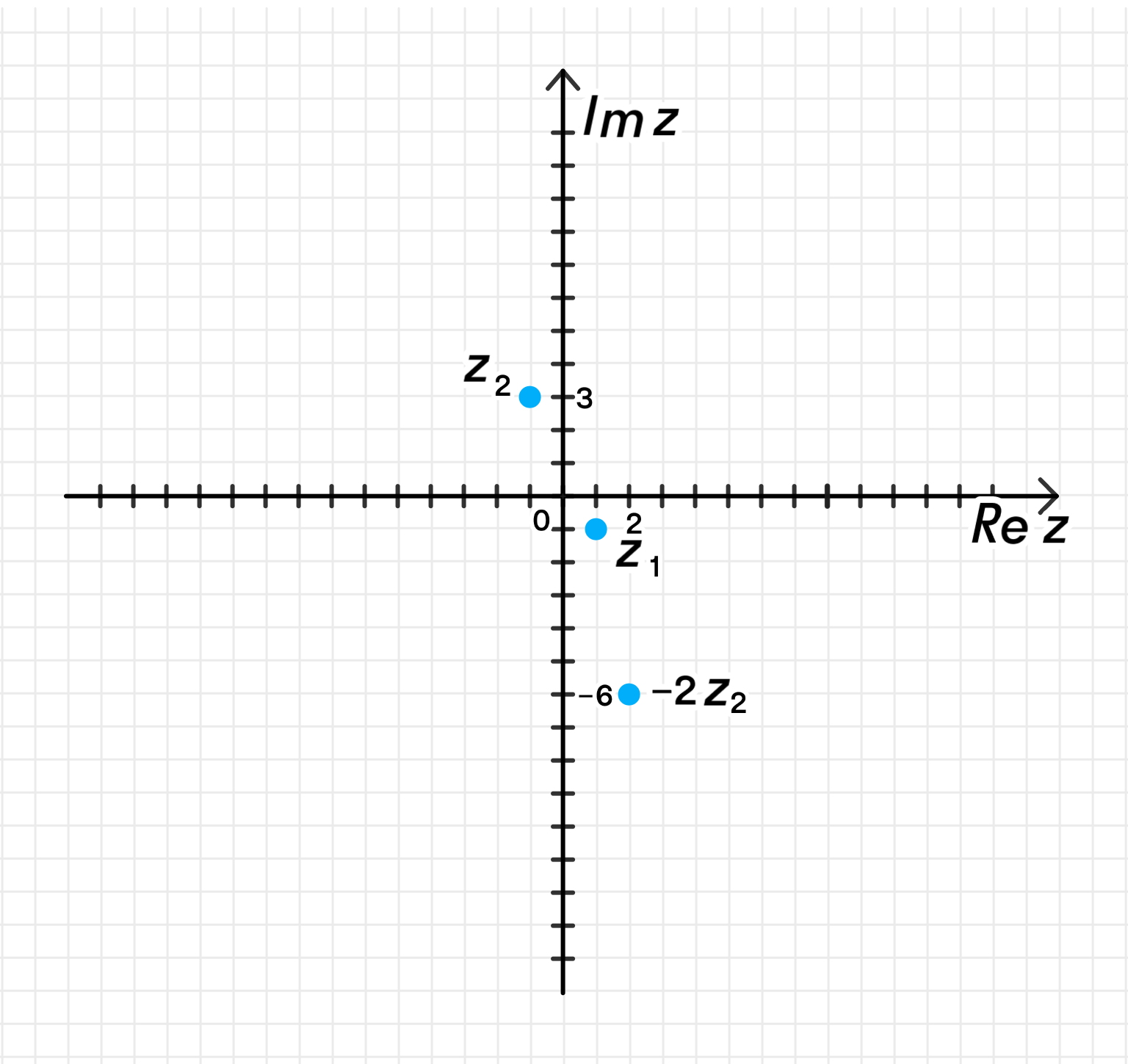Алгебра Профильный Уровень
10 класс задачник профильный уровень Мордкович
10 класс
Тип
ГДЗ, Решебник.
Автор
А.Г. Мордкович, П. В. Семенов.
Год
2015-2020.
Издательство
Мнемозина.
Описание
Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 33.13 Профильный Уровень Мордкович — Подробные Ответы
Задача
Известите на координатной плоскости числа и , а также числа:
а) ;
б) ;
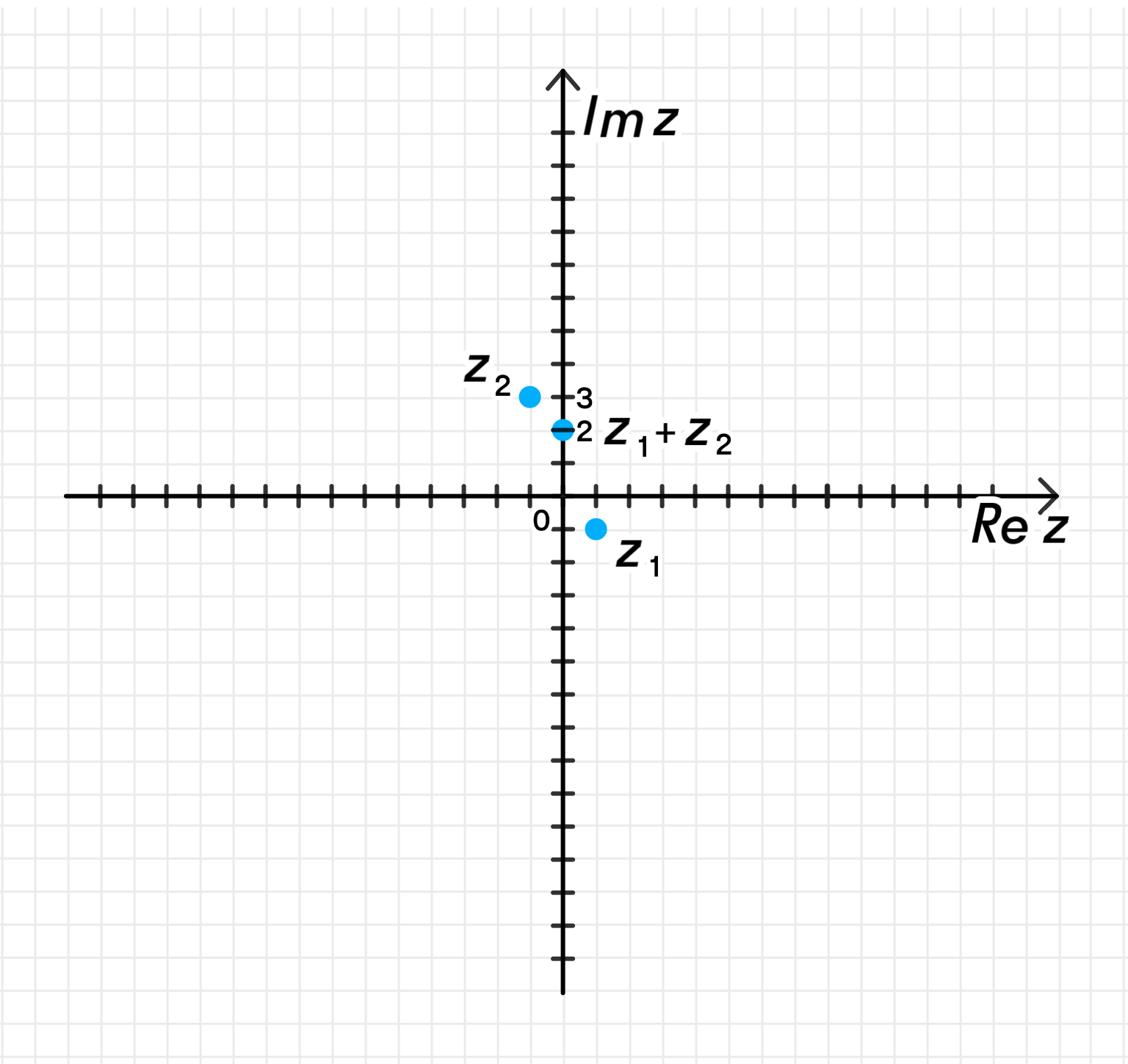
в) ;
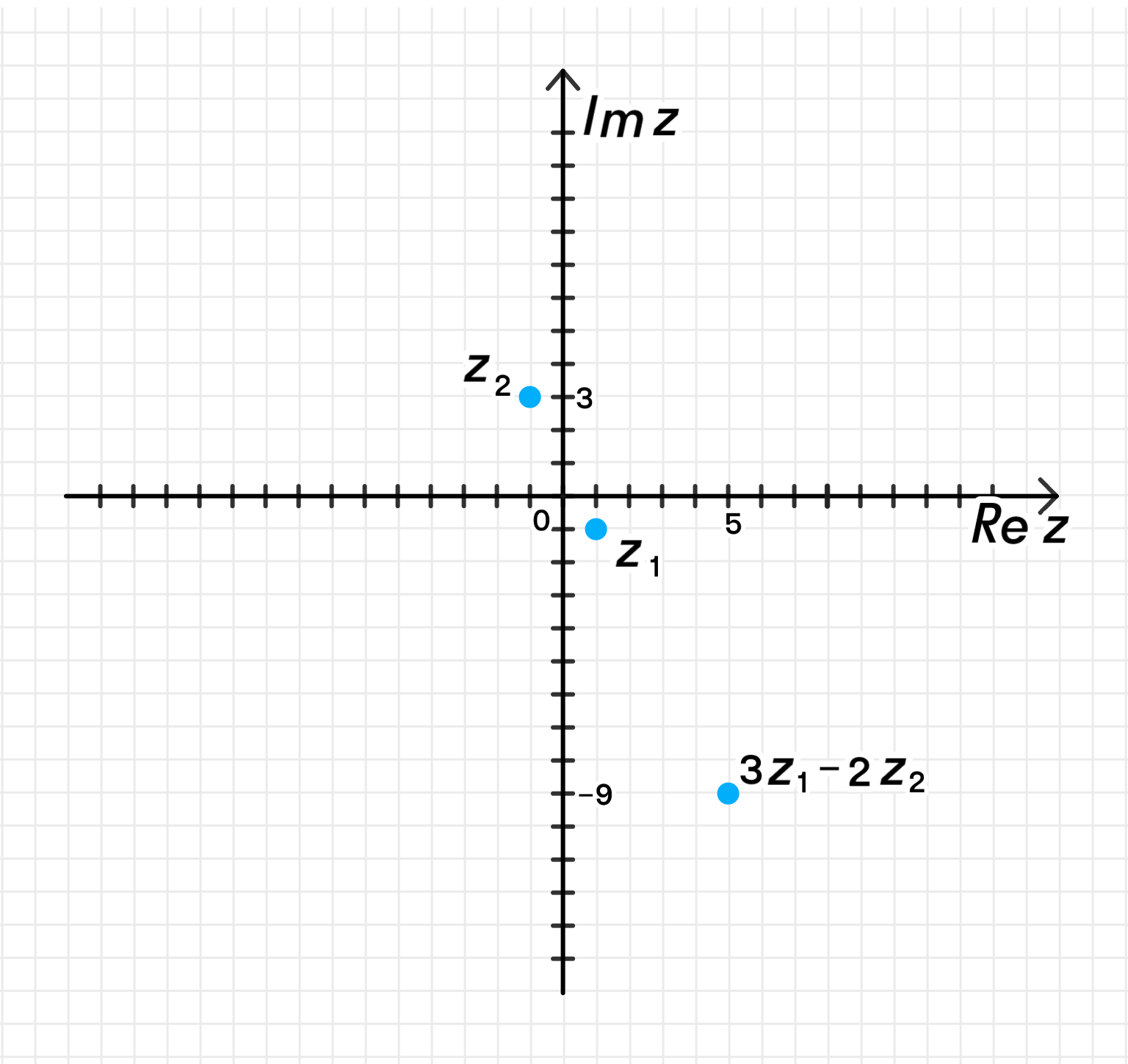
г) .
Подробный ответ:
Шаг 1: Понимание комплексных чисел
Любое комплексное число можно представить в виде:
где:
- — действительная часть (ось X),
- — мнимая часть (ось Y).
Таким образом:
- соответствует точке ,
- соответствует точке .
Шаг 2: Найдем выражения
а)
Умножим на 3:
Это точка .
б)
Умножим на -2:
Это точка .
в)
Сложим и :
Это точка .
г)
Воспользуемся уже найденными значениями:
Теперь:
Это точка .
Шаг 3: Таблица значений
| Обозначение | Формула | Комплексное число | Координаты на плоскости |
|---|---|---|---|
Комментарии
Другие предметы