ГДЗ по Алгебре 10 Класс Номер 33.15 Профильный Уровень Мордкович — Подробные Ответы

а) Изобразите на координатной плоскости числа $z_1 = -3 + i$ и $z_2 = 5 + 2i$.

б) Найдите действительный коэффициент $a$, при котором $z_1 + az_2$ — чисто мнимое число.

в) По правилу параллелограмма постройте сумму чисел $z_1$ и $az_2$ из пункта б).

г) Найдите действительный коэффициент $a$, при котором $z_1 + az_2$ — действительное число; по правилу параллелограмма постройте сумму чисел $z_1$ и $az_2$.

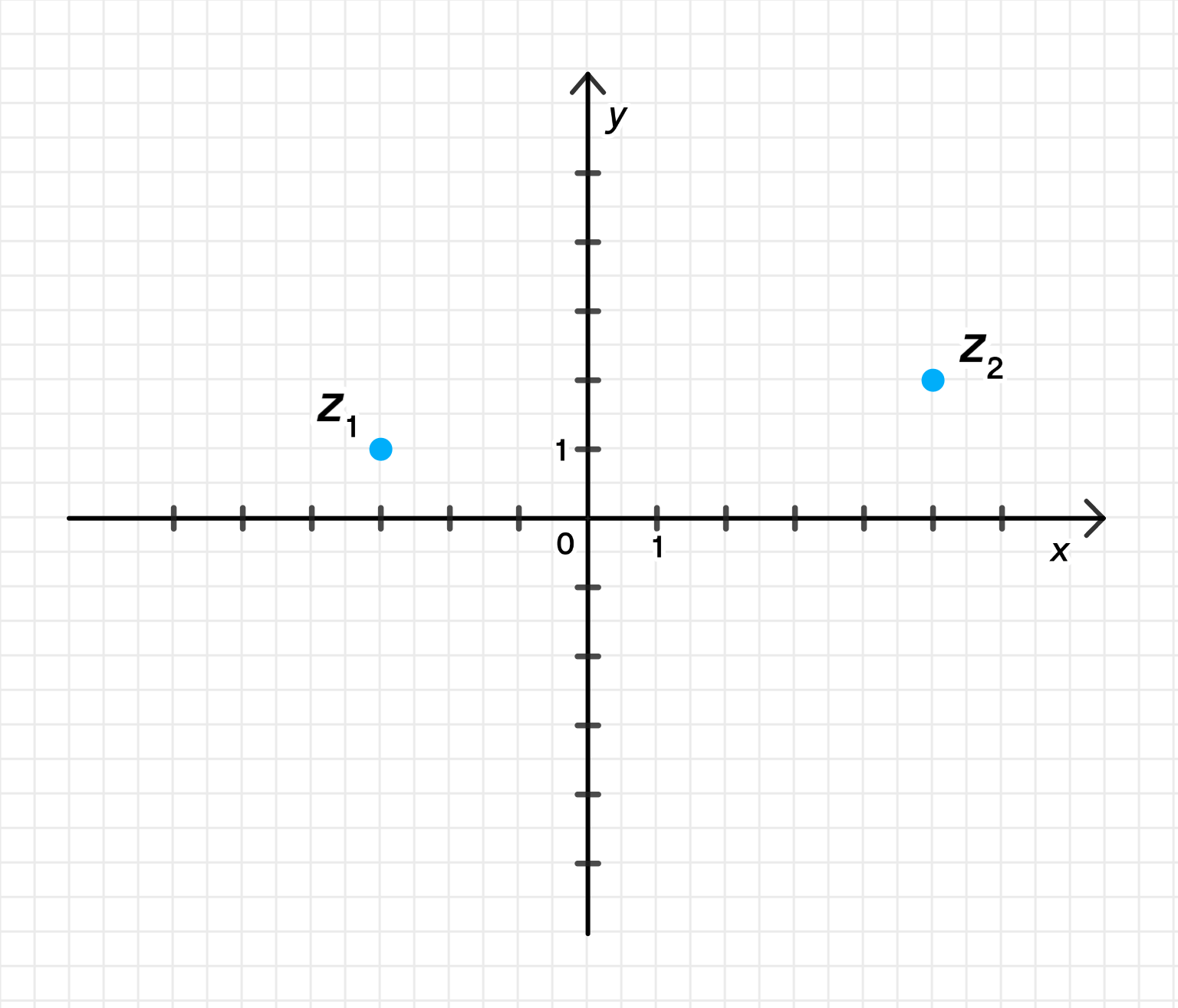
а) Изобразим на координатной плоскости числа:

$$z_1 = -3 + i \quad \text{и} \quad z_2 = 5 + 2i;$$

б) Число $z_1 + az_2$ является чисто мнимым при:

$$z_1 + az_2 = (-3 + i) + a(5 + 2i) = (5a — 3) + (2a + 1)i;$$ $$5a — 3 = 0;$$ $$5a = 3;$$ $$a = \frac{3}{5};$$

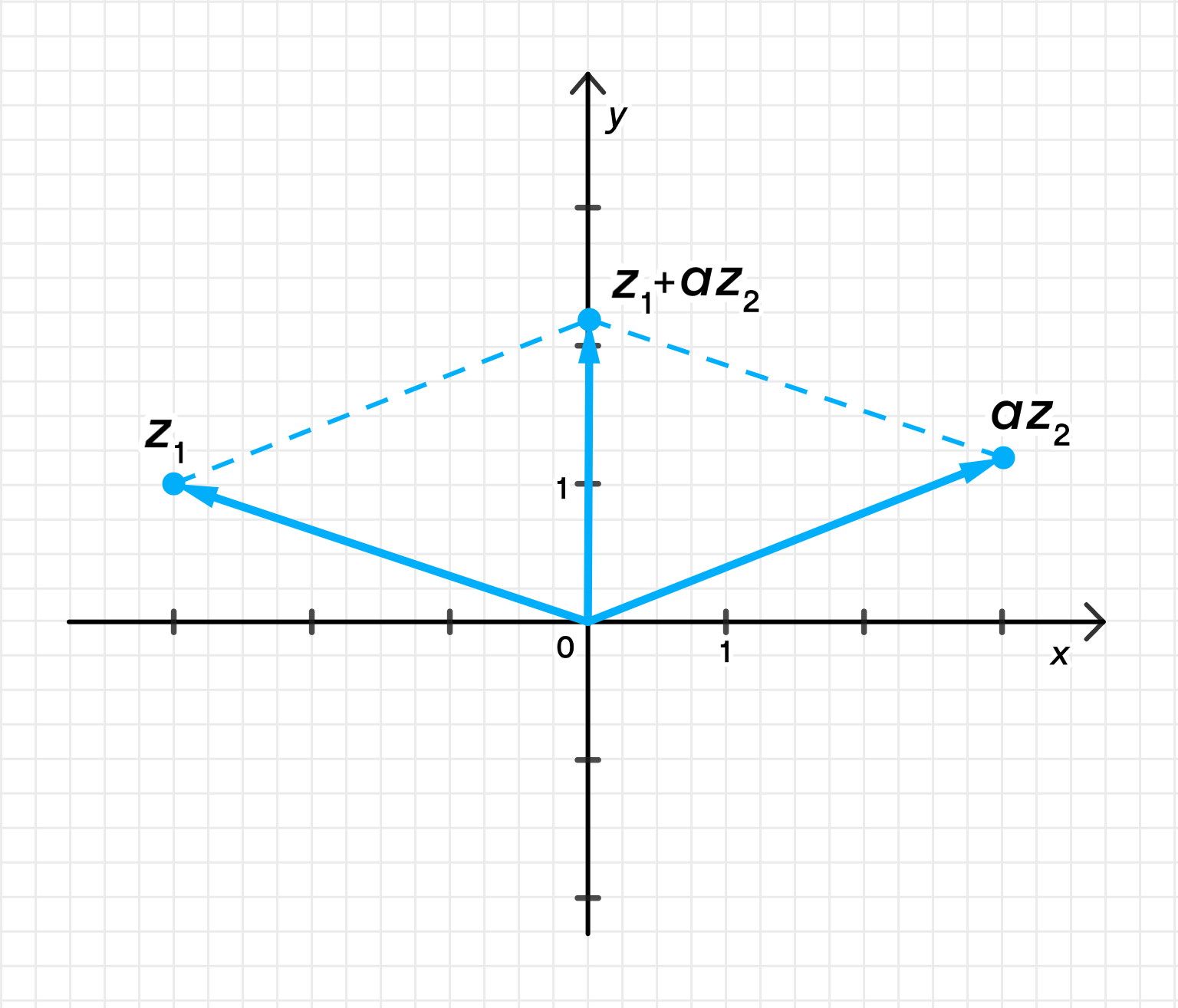
в) Построим сумму чисел $z_1$ и $az_2$ из пункта б:

$$z_1 + az_2 = (-3 + i) + \frac{3}{5}(5 + 2i) = (-3 + i) + (3 + \frac{6}{5}i) = 0 + \left(1 + \frac{6}{5}\right)i = \frac{11}{5}i.$$

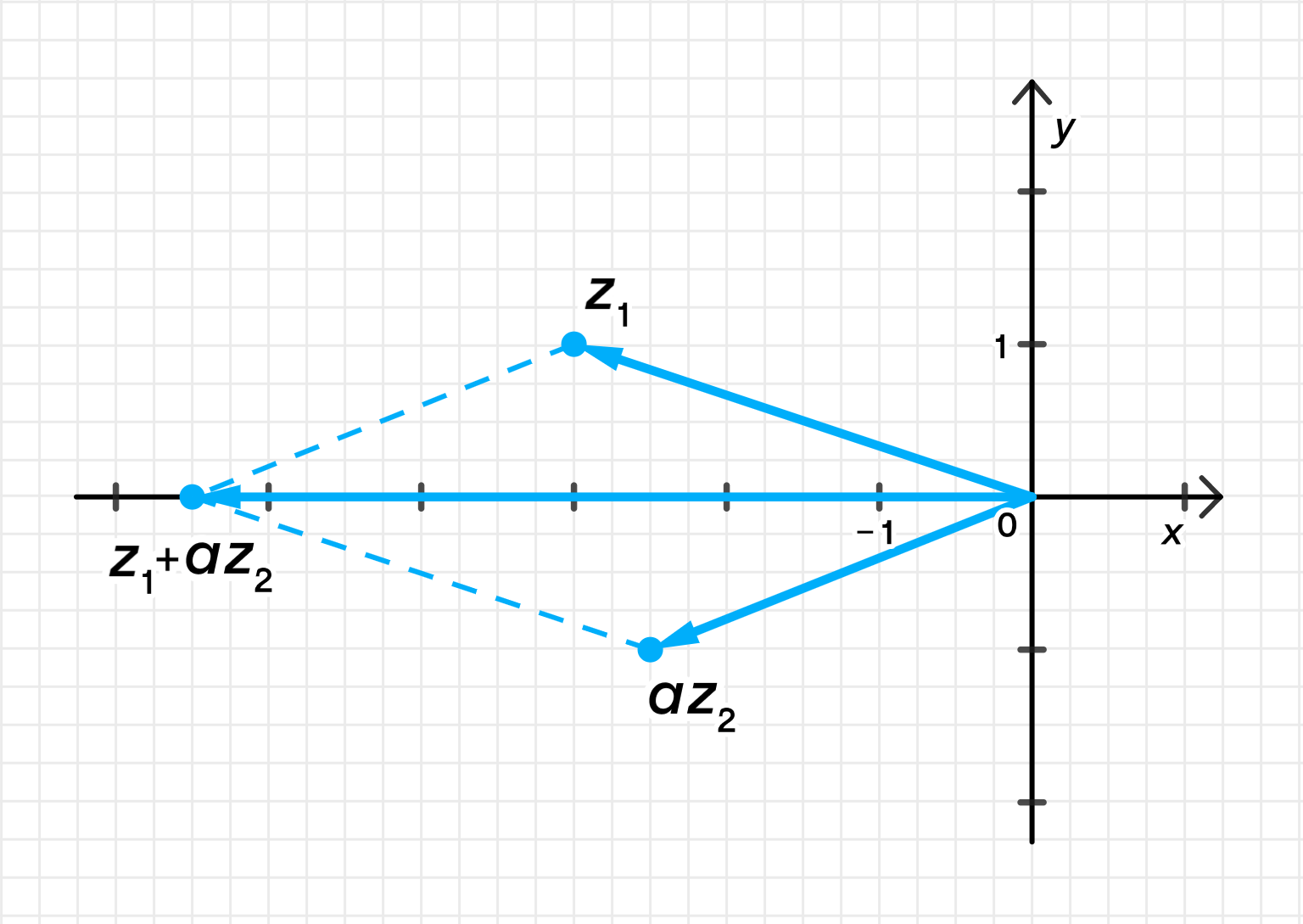
г) Число $z_1 + az_2$ является действительным при:

$$z_1 + az_2 = (-3 + i) + a(5 + 2i) = (5a — 3) + (2a + 1)i;$$ $$2a + 1 = 0;$$ $$2a = -1;$$ $$a = -\frac{1}{2};$$

Комплексные числа:

$$z_1 = -3 + i, \quad z_2 = 5 + 2i$$

а) Изобразим на координатной плоскости числа $z_1$ и $z_2$

Представление:

Каждое комплексное число $z = a + bi$ можно представить точкой $(a, b)$ на координатной плоскости:

• $z_1 = -3 + i \Rightarrow (-3, 1)$
• $z_2 = 5 + 2i \Rightarrow (5, 2)$

Будем строить это на комплексной плоскости:

• ось X — действительная часть (Re)
• ось Y — мнимая часть (Im)

б) Найдём $a$, при котором число $z_1 + a z_2$ является чисто мнимым

Шаг 1: Выразим сумму

$$z_1 + a z_2 = (-3 + i) + a(5 + 2i)$$

Раскроем скобки:

$$= -3 + i + 5a + 2a i$$

Соберём по действительной и мнимой частям:

$$= (5a — 3) + (2a + 1)i$$

Шаг 2: Условие чисто мнимого числа

Число чисто мнимое, если действительная часть равна нулю, т.е.:

$$5a — 3 = 0$$

Решим:

$$5a = 3 \quad \Rightarrow \quad a = \frac{3}{5}$$

в) Подставим $a = \frac{3}{5}$ и найдём сумму $z_1 + az_2$

Шаг 1: Подставим:

$$z_1 + \frac{3}{5} z_2 = (-3 + i) + \frac{3}{5}(5 + 2i)$$

Шаг 2: Раскроем скобки:

$$= -3 + i + 3 + \frac{6}{5}i$$

Сложим:

• Действительная часть: $-3 + 3 = 0$
• Мнимая часть: $i + \frac{6}{5}i = \left(1 + \frac{6}{5}\right)i = \frac{11}{5}i$

Результат:

$$z_1 + \frac{3}{5} z_2 = \frac{11}{5}i$$

Это действительно чисто мнимое число, как и ожидалось.

г) Найдём $a$, при котором $z_1 + a z_2$ является действительным

Шаг 1: Выражение уже есть:

$$z_1 + az_2 = (5a — 3) + (2a + 1)i$$

Шаг 2: Условие действительности:

Число действительное, если мнимая часть равна нулю, т.е.:

$$2a + 1 = 0$$

Решим:

$$2a = -1 \quad \Rightarrow \quad a = -\frac{1}{2}$$