Задача
а) Для n = 1 , 2 , 3 , 4 n = 1, 2, 3, 4 z n = ( 2 n − 1 ) + ( 5 − n ) i z_n = (2n — 1) + (5 — n)i
б) докажите, что все эти точки лежат на одной прямой l l
в) укажите число, лежащее на прямой l l Re z = − 5 \text{Re } z = -5
г) укажите число, лежащее на прямой l l Im z = 8 \text{Im } z = 8
Краткий ответ:
Даны комплексные числа:
z n = ( 2 n − 1 ) + ( 5 − n ) i ; z_n = (2n — 1) + (5 — n)i;
а) Для чисел n = 1 , 2 , 3 , 4 n = 1, 2, 3, 4
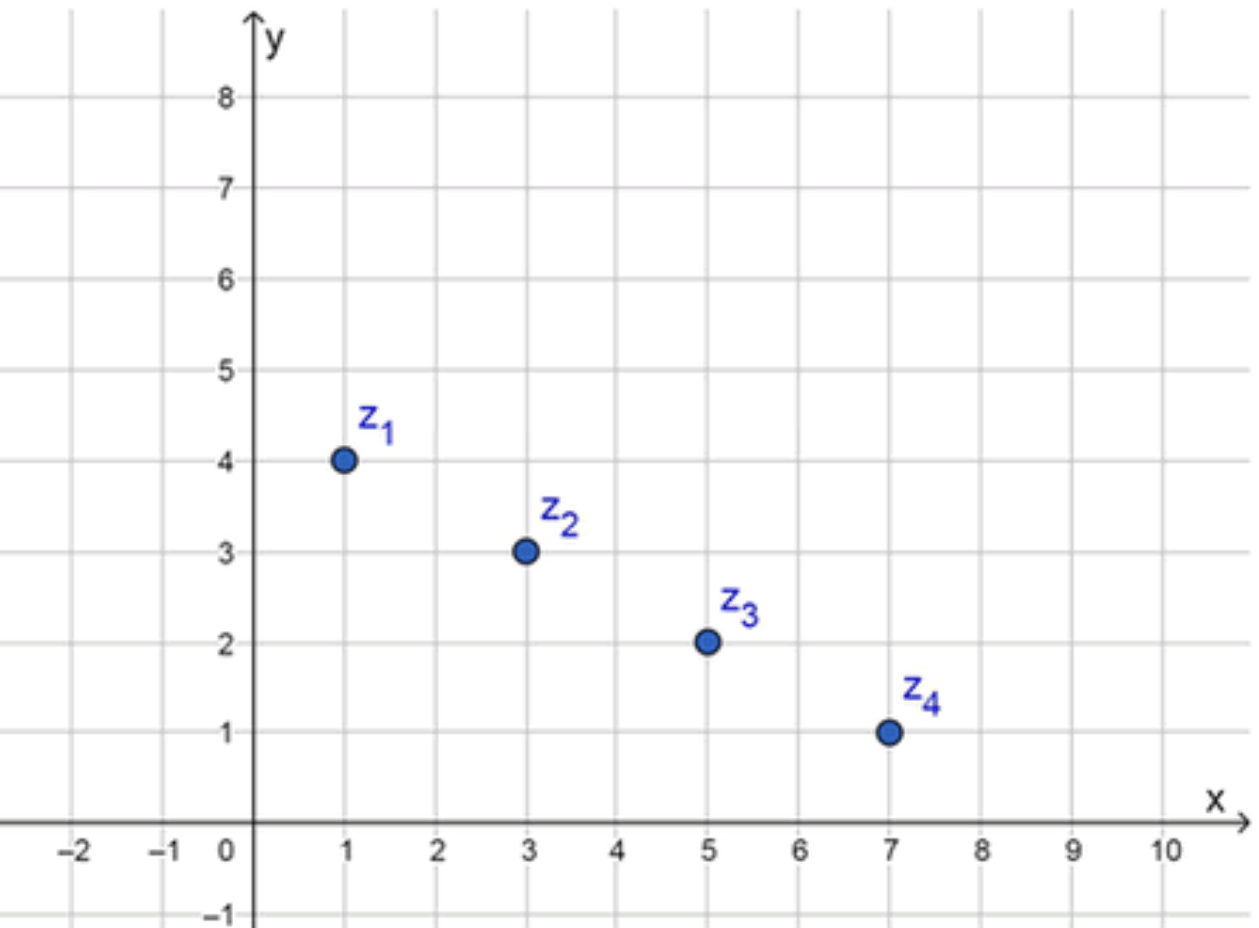
z 1 = ( 2 ⋅ 1 − 1 ) + ( 5 − 1 ) i = 1 + 4 i ; z_1 = (2 \cdot 1 — 1) + (5 — 1)i = 1 + 4i; z 2 = ( 2 ⋅ 2 − 1 ) + ( 5 − 2 ) i = 3 + 3 i ; z_2 = (2 \cdot 2 — 1) + (5 — 2)i = 3 + 3i; z 3 = ( 2 ⋅ 3 − 1 ) + ( 5 − 3 ) i = 5 + 2 i ; z_3 = (2 \cdot 3 — 1) + (5 — 3)i = 5 + 2i; z 4 = ( 2 ⋅ 4 − 1 ) + ( 5 − 4 ) i = 7 + i ; z_4 = (2 \cdot 4 — 1) + (5 — 4)i = 7 + i;
б) Докажем, что все точки лежат на одной прямой l l
x = 2 n − 1 ; x = 2n — 1; 2 n = x + 1 ; 2n = x + 1; n = 0.5 x + 0.5 ; n = 0.5x + 0.5; y = 5 − n = 5 − ( 0.5 x + 0.5 ) = 4.5 − 0.5 x ; y = 5 — n = 5 — (0.5x + 0.5) = 4.5 — 0.5x;
Ответ: y = 4.5 − 0.5 x y = 4.5 — 0.5x
в) Число, лежащее на прямой l l Re z = − 5 \text{Re } z = -5
x = − 5 ; x = -5; y = 4.5 − 0.5 ⋅ ( − 5 ) = 4.5 + 2.5 = 7 ; y = 4.5 — 0.5 \cdot (-5) = 4.5 + 2.5 = 7;
Ответ: z = − 5 + 7 i z = -5 + 7i
г) Число, лежащее на прямой l l Im z = 8 \text{Im } z = 8
y = 8 ; y = 8; 4.5 − 0.5 x = 8 ; 4.5 — 0.5x = 8; 0.5 x = − 3.5 ; 0.5x = -3.5; x = − 7 ; x = -7;
Ответ: z = − 7 + 8 i z = -7 + 8i
Подробный ответ:
Даны комплексные числа:
z n = ( 2 n − 1 ) + ( 5 − n ) i z_n = (2n — 1) + (5 — n)i
где n n
Каждое такое число имеет действительную часть x = 2 n − 1 x = 2n — 1 мнимую часть y = 5 − n y = 5 — n
а) Для чисел n = 1 , 2 , 3 , 4 n = 1, 2, 3, 4
Напомним:
Комплексное число z = x + y i z = x + yi ( x , y ) (x, y)
Для n = 1 n = 1
z 1 = ( 2 ⋅ 1 − 1 ) + ( 5 − 1 ) i = 1 + 4 i z_1 = (2 \cdot 1 — 1) + (5 — 1)i = 1 + 4i
Координаты точки: ( 1 , 4 ) (1, 4)
Для n = 2 n = 2
z 2 = ( 2 ⋅ 2 − 1 ) + ( 5 − 2 ) i = 3 + 3 i z_2 = (2 \cdot 2 — 1) + (5 — 2)i = 3 + 3i
Координаты точки: ( 3 , 3 ) (3, 3)
Для n = 3 n = 3
z 3 = ( 2 ⋅ 3 − 1 ) + ( 5 − 3 ) i = 5 + 2 i z_3 = (2 \cdot 3 — 1) + (5 — 3)i = 5 + 2i
Координаты точки: ( 5 , 2 ) (5, 2)
Для n = 4 n = 4
z 4 = ( 2 ⋅ 4 − 1 ) + ( 5 − 4 ) i = 7 + i z_4 = (2 \cdot 4 — 1) + (5 — 4)i = 7 + i
Координаты точки: ( 7 , 1 ) (7, 1)
Вывод:
Все точки:
z 1 = ( 1 , 4 ) z_1 = (1, 4) z 2 = ( 3 , 3 ) z_2 = (3, 3) z 3 = ( 5 , 2 ) z_3 = (5, 2) z 4 = ( 7 , 1 ) z_4 = (7, 1)
б) Докажем, что все точки лежат на одной прямой l l
Нам нужно показать, что точки z n z_n x x y y n n n n y = k x + b y = kx + b
Шаг 1: Даны зависимости от n n
x = 2 n − 1 и y = 5 − n x = 2n — 1 \quad \text{и} \quad y = 5 — n
Шаг 2: Выразим n n x x
Из уравнения:
x = 2 n − 1 ⇒ 2 n = x + 1 ⇒ n = x + 1 2 x = 2n — 1 \Rightarrow 2n = x + 1 \Rightarrow n = \frac{x + 1}{2}
Шаг 3: Подставим n n y y
y = 5 − n = 5 − ( x + 1 2 ) = 10 − ( x + 1 ) 2 = 9 − x 2 y = 5 — n = 5 — \left(\frac{x + 1}{2}\right) = \frac{10 — (x + 1)}{2} = \frac{9 — x}{2} ⇒ y = 4.5 − 0.5 x \Rightarrow y = 4.5 — 0.5x
Уравнение прямой l l
y = 4.5 − 0.5 x y = 4.5 — 0.5x
Это прямая с наклоном − 0.5 -0.5
в) Число, лежащее на прямой l l Re z = − 5 \text{Re } z = -5
Задано:
x = Re z = − 5 x = \text{Re } z = -5
Ищем соответствующее значение y y
y = 4.5 − 0.5 x = 4.5 − 0.5 ⋅ ( − 5 ) = 4.5 + 2.5 = 7 y = 4.5 — 0.5x = 4.5 — 0.5 \cdot (-5) = 4.5 + 2.5 = 7
Значит:
z = − 5 + 7 i z = -5 + 7i
г) Число, лежащее на прямой l l Im z = 8 \text{Im } z = 8
Задано:
y = Im z = 8 y = \text{Im } z = 8
Ищем x x
y = 4.5 − 0.5 x ⇒ 8 = 4.5 − 0.5 x y = 4.5 — 0.5x \Rightarrow 8 = 4.5 — 0.5x
Решим:
0.5 x = 4.5 − 8 = − 3.5 ⇒ x = − 7 0.5x = 4.5 — 8 = -3.5 \Rightarrow x = -7
Значит:
z = − 7 + 8 i z = -7 + 8i
Окончательные ответы:
а)
z 1 = 1 + 4 i z 2 = 3 + 3 i z 3 = 5 + 2 i z 4 = 7 + i \begin{align*} z_1 &= 1 + 4i \\ z_2 &= 3 + 3i \\ z_3 &= 5 + 2i \\ z_4 &= 7 + i \end{align*}
б)
y = 4.5 − 0.5 x y = 4.5 — 0.5x
в) Re z = − 5 \text{Re } z = -5
z = − 5 + 7 i z = -5 + 7i
г) Im z = 8 \text{Im } z = 8
z = − 7 + 8 i z = -7 + 8i