Задача
а) Для n = 1 , 2 , 3 , 4 , 5 , 6 n = 1, 2, 3, 4, 5, 6 z n = ( n − 1 ) + ( n 2 − 5 n + 6 ) i z_n = (n-1) + (n^2 — 5n + 6)i
б) Докажите, что эти точки лежат на одной параболе; составьте уравнение параболы.
в) Найдите действительную часть суммы z 1 + z 2 + … + z 6 z_1 + z_2 + \ldots + z_6
г) Укажите наименьший номер n n z n z_n
Краткий ответ:
Даны комплексные числа:
z n = ( n − 1 ) + ( n 2 − 5 n + 6 ) i ; z_n = (n-1) + (n^2 — 5n + 6)i;
а) Для чисел n = 1 , 2 , 3 , 4 , 5 , 6 n = 1, 2, 3, 4, 5, 6
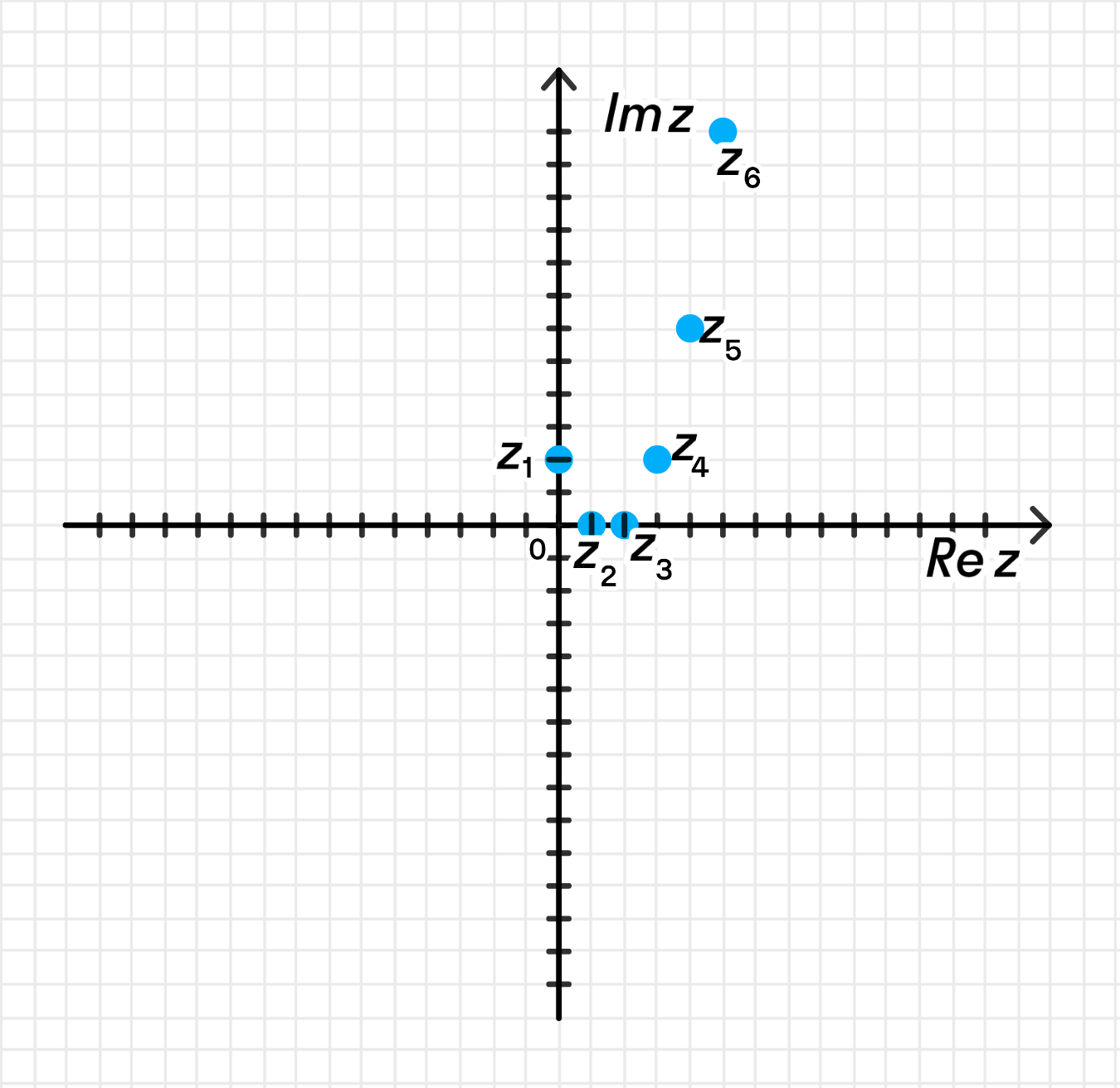
z 1 = ( 1 − 1 ) + ( 1 − 5 + 6 ) i = 2 i ; z_1 = (1-1) + (1-5+6)i = 2i; z 2 = ( 2 − 1 ) + ( 4 − 10 + 6 ) i = 1 ; z_2 = (2-1) + (4-10+6)i = 1; z 3 = ( 3 − 1 ) + ( 9 − 15 + 6 ) i = 2 ; z_3 = (3-1) + (9-15+6)i = 2; z 4 = ( 4 − 1 ) + ( 16 − 20 + 6 ) i = 3 + 2 i ; z_4 = (4-1) + (16-20+6)i = 3 + 2i; z 5 = ( 5 − 1 ) + ( 25 − 25 + 6 ) i = 4 + 6 i ; z_5 = (5-1) + (25-25+6)i = 4 + 6i; z 6 = ( 6 − 1 ) + ( 36 − 30 + 6 ) i = 5 + 12 i ; z_6 = (6-1) + (36-30+6)i = 5 + 12i;
б) Докажем, что все точки лежат на одной параболе:
x = n − 1 ; x = n — 1; n = x + 1 ; n = x + 1; y = n 2 − 5 n + 6 = ( x + 1 ) 2 − 5 ( x + 1 ) + 6 ; y = n^2 — 5n + 6 = (x+1)^2 — 5(x+1) + 6; y = x 2 + 2 x + 1 − 5 x − 5 + 6 = x 2 − 3 x + 2 ; y = x^2 + 2x + 1 — 5x — 5 + 6 = x^2 — 3x + 2;
Ответ: y = x 2 − 3 x + 2 y = x^2 — 3x + 2
в) Действительная часть суммы z 1 + z 2 + ⋯ + z 6 z_1 + z_2 + \cdots + z_6
( 1 − 1 ) + ( 2 − 1 ) + ⋯ + ( 6 − 1 ) = 0 + 1 + 2 + 3 + 4 + 5 = 15 ; (1-1) + (2-1) + \cdots + (6-1) = 0 + 1 + 2 + 3 + 4 + 5 = 15;
Ответ: 15.
г) Наименьший номер n n Im z > 100 \text{Im } z > 100
n 2 − 5 n + 6 > 100 ; n^2 — 5n + 6 > 100; n 2 − 5 n − 94 > 0 ; n^2 — 5n — 94 > 0; D = 5 2 + 4 ⋅ 94 = 25 + 376 = 401 ≈ 400 , тогда: D = 5^2 + 4 \cdot 94 = 25 + 376 = 401 \approx 400, \text{ тогда: } n 1 ≈ 5 − 20 2 = − 7.5 и n 2 ≈ 5 + 20 2 = 12.5 ; n_1 \approx \frac{5 — 20}{2} = -7.5 \quad \text{и} \quad n_2 \approx \frac{5 + 20}{2} = 12.5; ( n + 7.5 ) ( n − 12.5 ) > 0 ; (n + 7.5)(n — 12.5) > 0; n < − 7.5 или n > 12.5 ; n < -7.5 \quad \text{или} \quad n > 12.5; n > 12.5 ; n > 12.5; n = 13 ; n = 13;
Ответ: 13.
Подробный ответ:
Даны комплексные числа:
z n = ( n − 1 ) + ( n 2 − 5 n + 6 ) i z_n = (n — 1) + (n^2 — 5n + 6)i
Это комплексное число имеет:
действительную часть : x = n − 1 x = n — 1 мнимую часть : y = n 2 − 5 n + 6 y = n^2 — 5n + 6 а) Для n = 1 , 2 , 3 , 4 , 5 , 6 n = 1, 2, 3, 4, 5, 6
Для каждого значения n n z n z_n
Для n = 1 n = 1
z 1 = ( 1 − 1 ) + ( 1 2 − 5 ⋅ 1 + 6 ) i = 0 + ( 1 − 5 + 6 ) i = 0 + 2 i = 2 i z_1 = (1 — 1) + (1^2 — 5 \cdot 1 + 6)i = 0 + (1 — 5 + 6)i = 0 + 2i = 2i
Координаты: ( 0 , 2 ) (0, 2)
Для n = 2 n = 2
z 2 = ( 2 − 1 ) + ( 4 − 10 + 6 ) i = 1 + 0 i = 1 z_2 = (2 — 1) + (4 — 10 + 6)i = 1 + 0i = 1
Координаты: ( 1 , 0 ) (1, 0)
Для n = 3 n = 3
z 3 = ( 3 − 1 ) + ( 9 − 15 + 6 ) i = 2 + 0 i = 2 z_3 = (3 — 1) + (9 — 15 + 6)i = 2 + 0i = 2
Координаты: ( 2 , 0 ) (2, 0)
Для n = 4 n = 4
z 4 = ( 4 − 1 ) + ( 16 − 20 + 6 ) i = 3 + 2 i z_4 = (4 — 1) + (16 — 20 + 6)i = 3 + 2i
Координаты: ( 3 , 2 ) (3, 2)
Для n = 5 n = 5
z 5 = ( 5 − 1 ) + ( 25 − 25 + 6 ) i = 4 + 6 i z_5 = (5 — 1) + (25 — 25 + 6)i = 4 + 6i
Координаты: ( 4 , 6 ) (4, 6)
Для n = 6 n = 6
z 6 = ( 6 − 1 ) + ( 36 − 30 + 6 ) i = 5 + 12 i z_6 = (6 — 1) + (36 — 30 + 6)i = 5 + 12i
Координаты: ( 5 , 12 ) (5, 12)
Итак, полученные точки:
n n
z n z_n Координаты ( x , y ) (x, y)
1
0 + 2 i 0 + 2i ( 0 , 2 ) (0, 2)
2
1 1 ( 1 , 0 ) (1, 0)
3
2 2 ( 2 , 0 ) (2, 0)
4 3 + 2 i 3 + 2i ( 3 , 2 ) (3, 2)
5
4 + 6 i 4 + 6i ( 4 , 6 ) (4, 6)
6 5 + 12 i 5 + 12i ( 5 , 12 ) (5, 12)
б) Докажем, что все точки лежат на одной параболе
Шаг 1: Введём обозначения
Пусть:
x = n − 1 ⇒ n = x + 1 x = n — 1 \Rightarrow n = x + 1 y = Im ( z n ) = n 2 − 5 n + 6 y = \text{Im}(z_n) = n^2 — 5n + 6 Шаг 2: Подставим n = x + 1 n = x + 1 y y
y = ( x + 1 ) 2 − 5 ( x + 1 ) + 6 y = (x + 1)^2 — 5(x + 1) + 6
Раскроем скобки:
( x + 1 ) 2 = x 2 + 2 x + 1 (x + 1)^2 = x^2 + 2x + 1 − 5 ( x + 1 ) = − 5 x − 5 -5(x + 1) = -5x — 5
Теперь:
y = x 2 + 2 x + 1 − 5 x − 5 + 6 = x 2 − 3 x + 2 y = x^2 + 2x + 1 — 5x — 5 + 6 = x^2 — 3x + 2
Уравнение параболы:
y = x 2 − 3 x + 2 y = x^2 — 3x + 2
Проверим подстановкой одной из точек, например x = 4 x = 4
y = 4 2 − 3 ⋅ 4 + 2 = 16 − 12 + 2 = 6 ⇒ ( 4 , 6 ) y = 4^2 — 3 \cdot 4 + 2 = 16 — 12 + 2 = 6 \Rightarrow (4, 6)
Совпадает с z 5 z_5
в) Найти действительную часть суммы z 1 + z 2 + z 3 + z 4 + z 5 + z 6 z_1 + z_2 + z_3 + z_4 + z_5 + z_6
Рассматриваем только действительные части z n z_n n − 1 n — 1
n n Re ( z n ) = n − 1 \text{Re}(z_n) = n — 1 1 0 2 1 3 2 4 3 5 4 6 5
Суммируем:
0 + 1 + 2 + 3 + 4 + 5 = 15 0 + 1 + 2 + 3 + 4 + 5 = 15
Ответ: 15
г) Найти наименьшее n n Im ( z n ) > 100 \text{Im}(z_n) > 100
Мнимая часть:
y = n 2 − 5 n + 6 > 100 ⇒ n 2 − 5 n − 94 > 0 y = n^2 — 5n + 6 > 100 \Rightarrow n^2 — 5n — 94 > 0
Решим квадратное неравенство:
Найдём корни уравнения:
n 2 − 5 n − 94 = 0 n^2 — 5n — 94 = 0
Вычислим дискриминант:
D = ( − 5 ) 2 − 4 ⋅ 1 ⋅ ( − 94 ) = 25 + 376 = 401 D = (-5)^2 — 4 \cdot 1 \cdot (-94) = 25 + 376 = 401
Корни:
n 1 , 2 = 5 ± 401 2 n_{1,2} = \frac{5 \pm \sqrt{401}}{2}
Приблизительно:
401 ≈ 20.02 ⇒ n 1 ≈ 5 − 20.02 2 ≈ − 7.51 , n 2 ≈ 5 + 20.02 2 ≈ 12.51 \sqrt{401} \approx 20.02 \Rightarrow n_1 \approx \frac{5 — 20.02}{2} \approx -7.51, \quad n_2 \approx \frac{5 + 20.02}{2} \approx 12.51
Решение неравенства:
n 2 − 5 n − 94 > 0 ⇒ n < − 7.51 или n > 12.51 n^2 — 5n — 94 > 0 \quad \Rightarrow \quad n < -7.51 \quad \text{или} \quad n > 12.51
Поскольку n ∈ N n \in \mathbb{N}
n = 13 n = 13
Ответ: 13