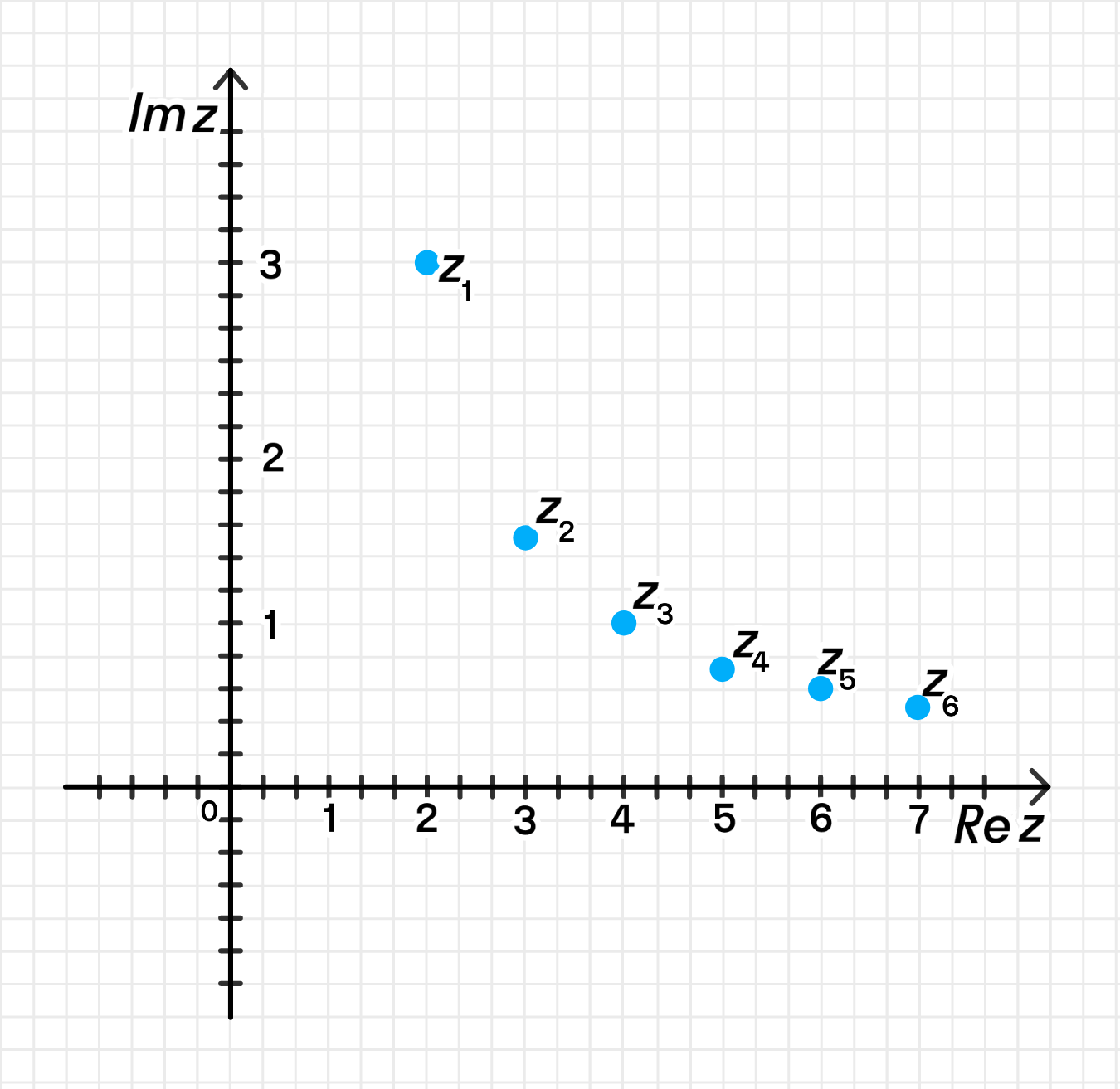ГДЗ по Алгебре 10 Класс Номер 33.19 Профильный Уровень Мордкович — Подробные Ответы

а) Для $n = 1, 2, 3, 4, 5, 6$ изобразите на координатной плоскости точки $z_n = (n + 1) + \frac{3}{n}i$.

б) Докажите, что все эти точки лежат на одной гиперболе; составьте уравнение гиперболы.

в) Укажите точку, наиболее близкую к оси абсцисс.

г) Укажите точку, наиболее близкую к началу координат.

Даны комплексные числа:

$$z_n = (n + 1) + \frac{3}{n}i;$$

а) Для чисел $n = 1, 2, 3, 4, 5, 6$ изобразим точки на плоскости:

$$z_1 = (1 + 1) + \frac{3}{1}i = 2 + 3i;$$ $$z_2 = (2 + 1) + \frac{3}{2}i = 3 + 1,5i;$$ $$z_3 = (3 + 1) + \frac{3}{3}i = 4 + i;$$ $$z_4 = (4 + 1) + \frac{3}{4}i = 5 + 0,75i;$$ $$z_5 = (5 + 1) + \frac{3}{5}i = 6 + 0,6i;$$ $$z_6 = (6 + 1) + \frac{3}{6}i = 7 + 0,5i;$$

б) Докажем, что все точки лежат на одной гиперболе:

$$x = n + 1;$$ $$n = x — 1;$$ $$y = \frac{3}{n} = \frac{3}{x — 1};$$

Ответ: $y = \frac{3}{x — 1}$.

в) Точка, наиболее близкая к оси абсцисс, то есть точка, имеющая наименьшую по модулю мнимую часть:

$$\text{Число } \frac{3}{n} \text{ — наименьшее;}$$ $$\text{Число } n \text{ — наибольшее;}$$ $$n = 6;$$

Ответ: $z_6 = 7 + 0,5i$.

г) Точка, наиболее близкая к началу координат:

$$d_1 = \sqrt{2^2 + 3^2} = \sqrt{4 + 9} = \sqrt{15};$$ $$d_2 = \sqrt{3^2 + 1,5^2} = \sqrt{9 + 2,25} = \sqrt{11,25};$$ $$d_3 = \sqrt{4^2 + 1^2} = \sqrt{16 + 1} = \sqrt{17};$$ $$d_4 = \sqrt{5^2 + 0,75^2} = \sqrt{25 + 0,75^2} > \sqrt{17};$$ $$d_5 = \sqrt{6^2 + 0,6^2} = \sqrt{36 + 0,36} > \sqrt{17};$$ $$d_6 = \sqrt{7^2 + 0,5^2} = \sqrt{49 + 0,25} > \sqrt{17};$$

Ответ: $z_2 = 3 + 1,5i$.

Даны комплексные числа:

$$z_n = (n + 1) + \frac{3}{n}i$$

Каждое число имеет:

• действительную часть: $x = n + 1$
• мнимую часть: $y = \dfrac{3}{n}$

а) Для $n = 1, 2, 3, 4, 5, 6$ изобразим точки на плоскости

Для каждого значения $n$ подставим в формулу и найдём число $z_n$.

$n = 1$:

$$z_1 = (1 + 1) + \frac{3}{1}i = 2 + 3i$$

Координаты: $(2, 3)$

$n = 2$:

$$z_2 = (2 + 1) + \frac{3}{2}i = 3 + 1.5i$$

Координаты: $(3, 1.5)$

$n = 3$:

$$z_3 = (3 + 1) + \frac{3}{3}i = 4 + 1i$$

Координаты: $(4, 1)$

$n = 4$:

$$z_4 = (4 + 1) + \frac{3}{4}i = 5 + 0.75i$$

Координаты: $(5, 0.75)$

$n = 5$:

$$z_5 = (5 + 1) + \frac{3}{5}i = 6 + 0.6i$$

Координаты: $(6, 0.6)$

$n = 6$:

$$z_6 = (6 + 1) + \frac{3}{6}i = 7 + 0.5i$$

Координаты: $(7, 0.5)$

Итоговая таблица:

б) Докажем, что все точки лежат на одной гиперболе

Идея — выразить координаты точек через $x$, избавиться от $n$, и получить зависимость $y = f(x)$.

Шаг 1:

Из формулы:

$$x = n + 1 \Rightarrow n = x — 1$$

Шаг 2:

Подставим $n = x — 1$ в выражение для $y$:

$$y = \frac{3}{n} = \frac{3}{x — 1}$$

Уравнение гиперболы:

$$y = \frac{3}{x — 1}$$

Проверка на одной из точек, например $x = 4$:

$$y = \frac{3}{4 — 1} = \frac{3}{3} = 1 \Rightarrow \text{совпадает с } z_3 = 4 + 1i$$

Условие выполнено.

в) Точка, наиболее близкая к оси абсцисс

Это означает: найти точку, у которой мнимая часть по модулю — наименьшая.

Мнимая часть:

$$y = \frac{3}{n} \Rightarrow y \text{ уменьшается с ростом } n$$

Наименьшее $\frac{3}{n}$ при наибольшем $n = 6$

Ответ:

$$z_6 = 7 + 0.5i$$

г) Точка, наиболее близкая к началу координат

Нужно найти точку, у которой модуль $|z_n| = \sqrt{x^2 + y^2}$ минимален.

Вычислим расстояние $d_n$ до начала координат:

$n = 1$:

$$d_1 = \sqrt{2^2 + 3^2} = \sqrt{4 + 9} = \sqrt{13} \approx 3.605$$

$n = 2$:

$$d_2 = \sqrt{3^2 + 1.5^2} = \sqrt{9 + 2.25} = \sqrt{11.25} \approx 3.354$$

$n = 3$:

$$d_3 = \sqrt{4^2 + 1^2} = \sqrt{16 + 1} = \sqrt{17} \approx 4.123$$

$n = 4$:

$$d_4 = \sqrt{5^2 + 0.75^2} = \sqrt{25 + 0.5625} = \sqrt{25.5625} \approx 5.056$$

$n = 5$:

$$d_5 = \sqrt{6^2 + 0.6^2} = \sqrt{36 + 0.36} = \sqrt{36.36} \approx 6.03$$

$n = 6$:

$$d_6 = \sqrt{7^2 + 0.5^2} = \sqrt{49 + 0.25} = \sqrt{49.25} \approx 7.02$$

Минимальное значение:

$$\sqrt{11.25} \approx 3.354 \Rightarrow \text{при } n = 2$$

Ответ:

$$z_2 = 3 + 1.5i$$