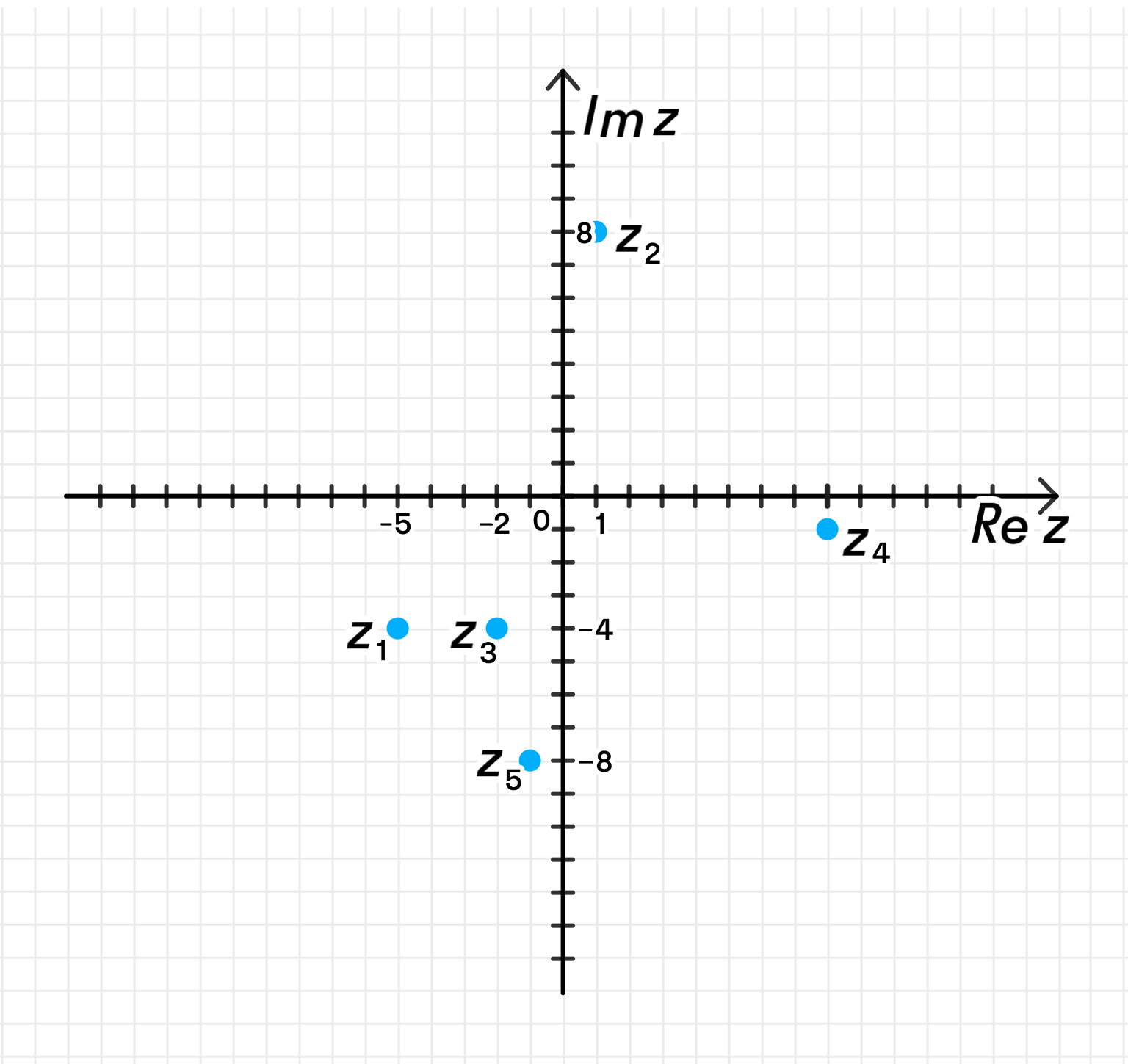ГДЗ по Алгебре 10 Класс Номер 33.2 Профильный Уровень Мордкович — Подробные Ответы

a) Отметьте на координатной плоскости точки, соответствующие комплексным числам $z_1=-5-4i,z_2=1+8i,z_3=-2-4i,z_4=8+i,z_5=-1-8\mathrm{i.}$

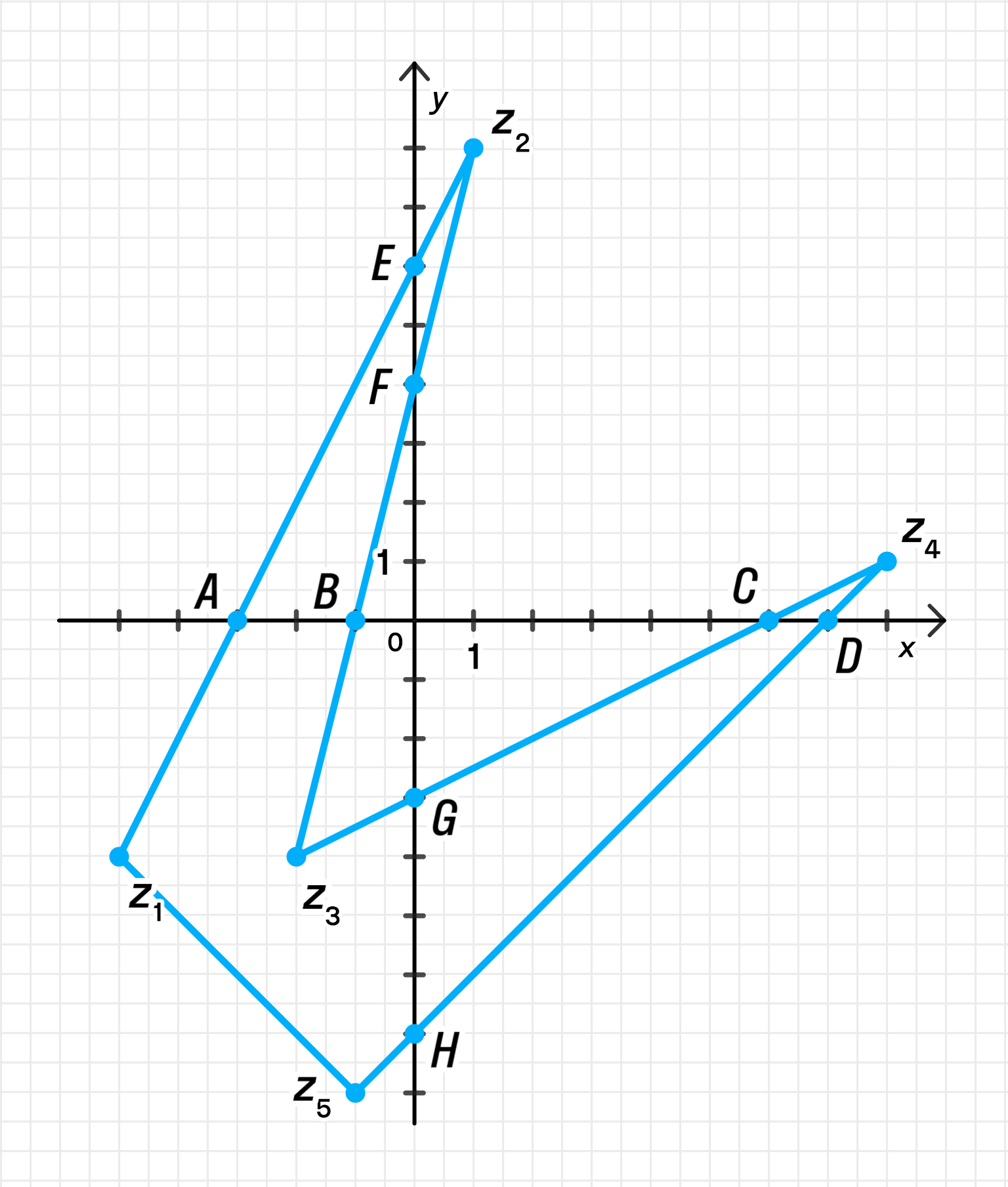
б) Соедините заданные точки последовательно отрезками. Сколько получилось точек пересечения с осями координат? Запишите комплексные числа, которым соответствуют эти точки.

Даны комплексные числа:
$z_1 = -5 — 4i, \quad z_2 = 1 + 8i, \quad z_3 = -2 — 4i, \quad z_4 = 8 + i, \quad z_5 = -1 — 8i;$

а) Данные точки на координатной плоскости:

б) Соединим последовательно данные точки отрезками:

Замкнутая ломаная имеет 8 пересечений с осями координат:
$z_6 = 0 + 4i = 4i;$
$z_7 = -1 + 0i = -1;$
$z_8 = -3 + 0i = -3;$
$z_9 = 0 — 3i = -3i;$
$z_{10} = 0 — 7i = -7i;$
$z_{11} = 6 + 0i = 6;$
$z_{12} = 7 + 0i = 7;$
$z_{13} = 0 + 6i = 6i;$

Даны комплексные числа:

$$z_1 = -5 — 4i, \quad z_2 = 1 + 8i, \quad z_3 = -2 — 4i, \quad z_4 = 8 + i, \quad z_5 = -1 — 8i$$

а) Построение точек на координатной плоскости

Комплексные числа имеют форму:

$$z = x + iy$$

где:

• $x$ — действительная часть (ось Re),
• $y$ — мнимая часть (ось Im).

Рассмотрим каждое число:

б) Построение замкнутой ломаной

Ломаная соединяет точки в порядке:

$$z_1 \rightarrow z_2 \rightarrow z_3 \rightarrow z_4 \rightarrow z_5 \rightarrow z_1$$

То есть, идут по следующей последовательности координат:

• $(-5, -4) \rightarrow (1, 8)$
• $(1, 8) \rightarrow (-2, -4)$
• $(-2, -4) \rightarrow (8, 1)$
• $(8, 1) \rightarrow (-1, -8)$
• $(-1, -8) \rightarrow (-5, -4)$

Пересечения с осями координат

Рассмотрим, какие отрезки (между двумя соседними точками) пересекают оси координат (ось $x$ и ось $y$).

Пересечения с осью $y$ (т.е. $x = 0$)

Для этого нужно найти, пересекает ли отрезок вертикальную прямую $x = 0$.

Отрезок $z_1 \rightarrow z_2$: от (–5, –4) до (1, 8)

• Δx = 6, Δy = 12 → проходит через $x = 0$

Найдём координаты точки пересечения:

$$x = -5 + 6t = 0 \Rightarrow t = \frac{5}{6}$$ $$y = -4 + 12 \cdot \frac{5}{6} = -4 + 10 = 6$$

Точка пересечения: $(0, 6) \Rightarrow z_{13} = 6i$

Отрезок $z_3 \rightarrow z_4$: (–2, –4) → (8, 1)

• Δx = 10 → пересекает $x = 0$

$$x = -2 + 10t = 0 \Rightarrow t = \frac{1}{5}$$ $$y = -4 + 5t = -4 + 1 = -3$$

Точка пересечения: $(0, -3) \Rightarrow z_9 = -3i$

Отрезок $z_5 \rightarrow z_1$: (–1, –8) → (–5, –4)

• Δx = –4 → не проходит через $x = 0$ (оба x < 0)

Не пересекает ось $y$

Отрезок $z_2 \rightarrow z_3$: (1, 8) → (–2, –4)

$$x = 1 — 3t = 0 \Rightarrow t = \frac{1}{3}$$ $$y = 8 — 12t = 8 — 4 = 4$$

Точка пересечения: $(0, 4) \Rightarrow z_6 = 4i$

Отрезок $z_4 \rightarrow z_5$: (8, 1) → (–1, –8)

$$x = 8 — 9t = 0 \Rightarrow t = \frac{8}{9}$$ $$y = 1 — 9t = 1 — 8 = -7$$

Точка пересечения: $(0, -7) \Rightarrow z_{10} = -7i$

Пересечения с осью $x$ (т.е. $y = 0$)

Отрезок $z_3 \rightarrow z_4$: (–2, –4) → (8, 1)

$$y = -4 + 5t = 0 \Rightarrow t = \frac{4}{5}$$ $$x = -2 + 10t = -2 + 8 = 6$$

Точка пересечения: $(6, 0) \Rightarrow z_{11} = 6$

Отрезок $z_2 \rightarrow z_3$: (1, 8) → (–2, –4)

$$y = 8 — 12t = 0 \Rightarrow t = \frac{2}{3}$$ $$x = 1 — 3t = 1 — 2 = -1$$

Точка пересечения: $(-1, 0) \Rightarrow z_7 = -1$

Отрезок $z_4 \rightarrow z_5$: (8, 1) → (–1, –8)

$$y = 1 — 9t = 0 \Rightarrow t = \frac{1}{9}$$ $$x = 8 — 9t = 8 — 1 = 7$$

Точка пересечения: $(7, 0) \Rightarrow z_{12} = 7$

Отрезок $z_5 \rightarrow z_1$: (–1, –8) → (–5, –4)

$$y = -8 + 4t = 0 \Rightarrow t = 2 \Rightarrow ❌ (вне отрезка)$$

Не пересекает

Отрезок $z_1 \rightarrow z_2$: (–5, –4) → (1, 8)

$$y = -4 + 12t = 0 \Rightarrow t = \frac{1}{3}$$ $$x = -5 + 6t = -5 + 2 = -3$$

Точка пересечения: $(-3, 0) \Rightarrow z_8 = -3$

Ответ: Все точки пересечения