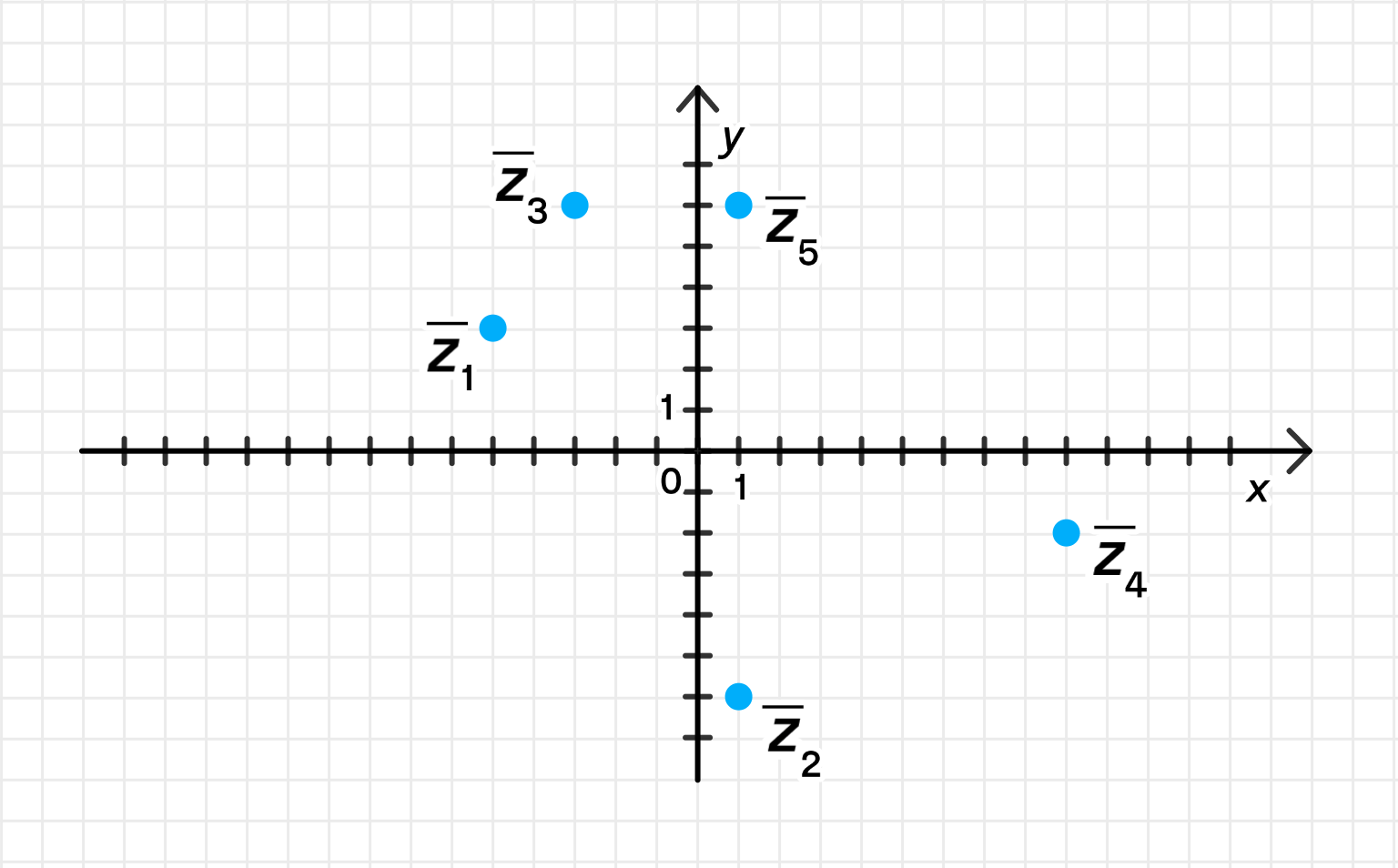ГДЗ по Алгебре 10 Класс Номер 33.3 Профильный Уровень Мордкович — Подробные Ответы

Даны комплексные числа:

$$z_1=-5-3i,z_2=1+6i,z_3=-3-6i,z_4=9+2i,z_5=1-6i;$$$${\bar{z}}_1=-5+3i,{\bar{z}}_2=1-6i,{\bar{z}}_3=-3+6i,{\bar{z}}_4=9-2i,{\bar{z}}_5=1+6i\mathrm{.}$$

а) Данные точки на координатной плоскости:

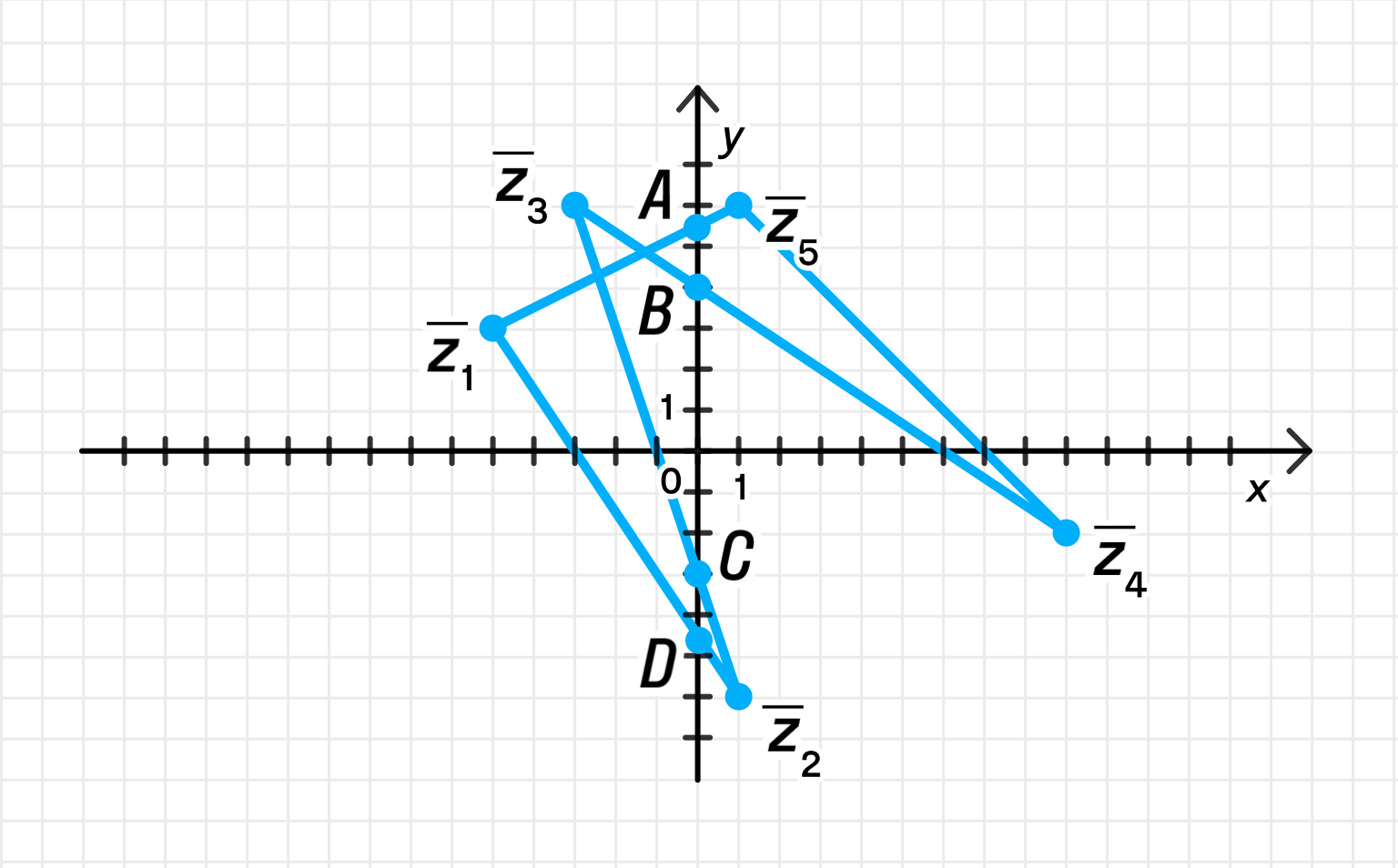
б) Соединим последовательно данные точки отрезками:

Ломаной принадлежит четыре чисто мнимых числа:

$$z_6=0+5.5i=5.5i;$$$$z_7=0+4i=4i;$$$$z_8=0-3i=-3i;$$$$z_9=0-4.5i=-4.5i;$$

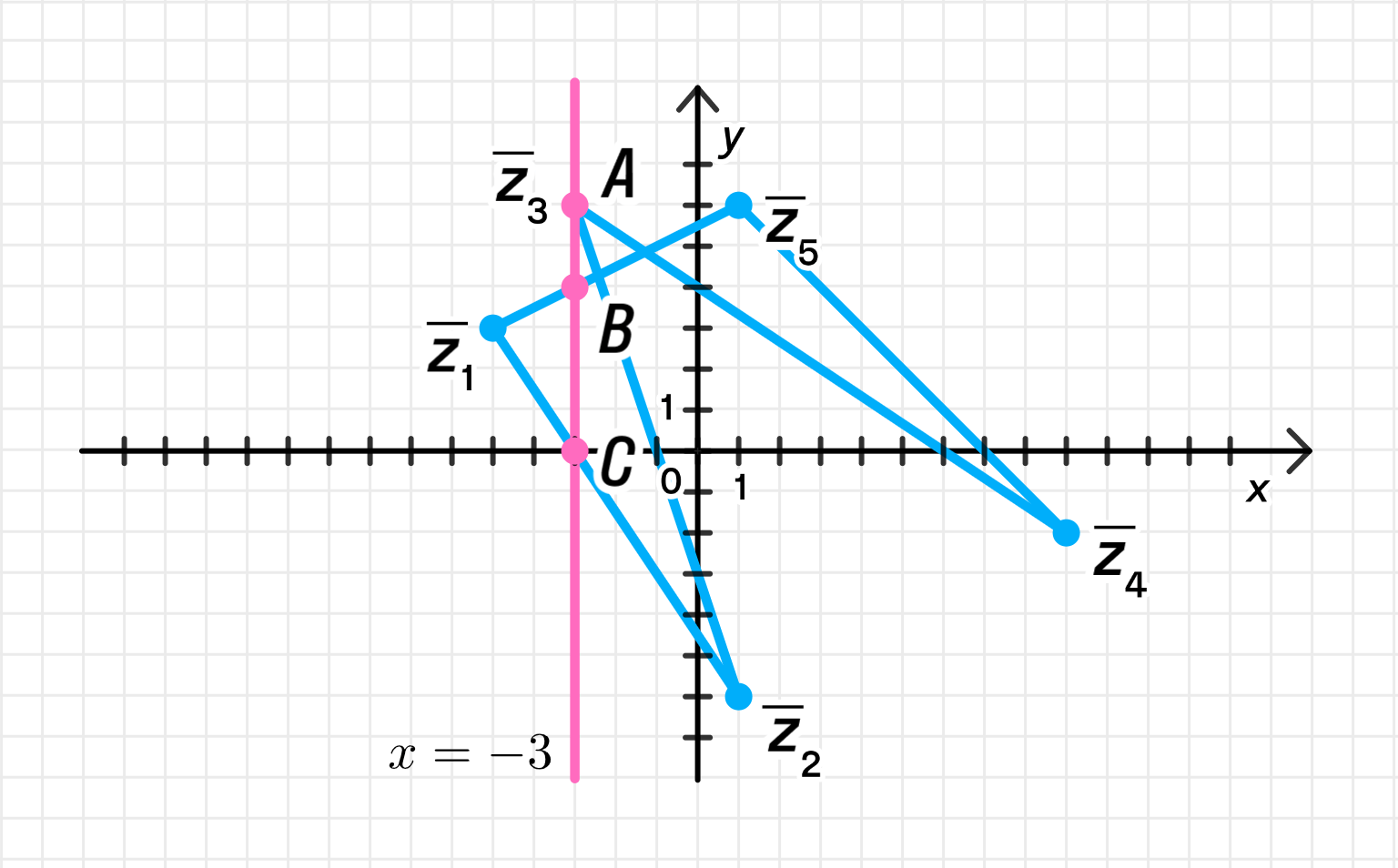
в) Отметим числа на этой ломаной, для которых $\text{Re }z=-3$:

Всего есть три таких точки:

$$z_3=-3+6i;$$$$z_6=-3+4i;$$$$z_7=-3+0i=-3;$$

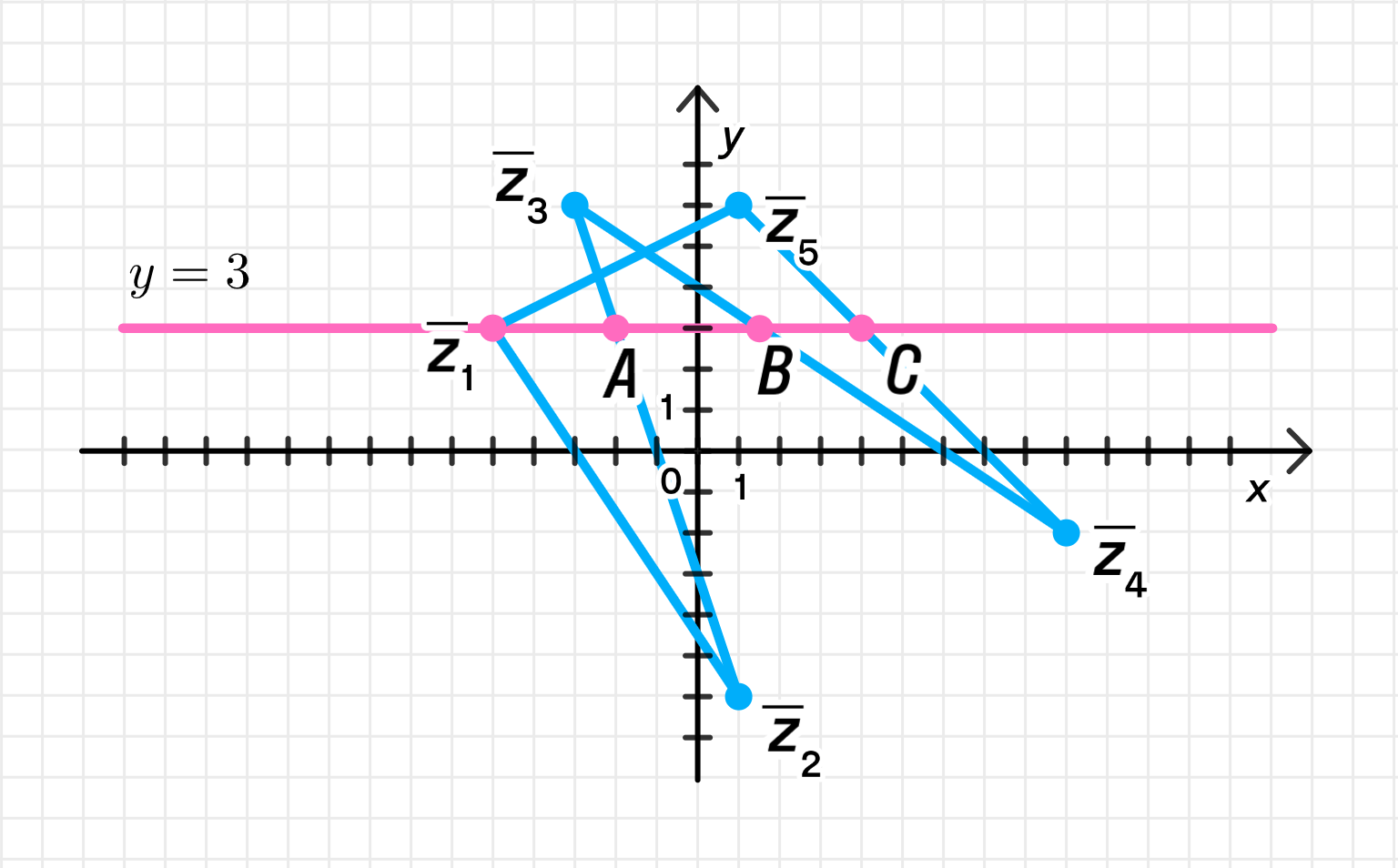
г) Отметим числа на этой ломаной, для которых $\text{Im }z=3$:

Всего есть четыре таких точки:

$${\bar{z}}_1=-5+3i;$$$$z_6=-2+3i;$$$$z_7=1.5+3i;$$$$z_8=4+3i$$

Комплексные числа:

$$z_1=-5-3i,z_2=1+6i,z_3=-3-6i,z_4=9+2i,z_5=1-6i$$

Комплексно-сопряжённые им числа:

$${\bar{z}}_1=-5+3i,{\bar{z}}_2=1-6i,{\bar{z}}_3=-3+6i,{\bar{z}}_4=9-2i,{\bar{z}}_5=1+6i$$

а) Построение точек ${\bar{z}}_1,{\bar{z}}_2,{\bar{z}}_3,{\bar{z}}_4,{\bar{z}}_5$ на координатной плоскости

Для любого комплексного числа $z=a+bi$, его геометрическое представление — это точка $(a,b)$, где:

• $a=\text{Re}(z)$ — действительная часть,
• $b=\text{Im}(z)$ — мнимая часть.

Точки:

1. ${\bar{z}}_1=-5+3i\to (-5,3)$
2. ${\bar{z}}_2=1-6i\to (1,-6)$
3. ${\bar{z}}_3=-3+6i\to (-3,6)$
4. ${\bar{z}}_4=9-2i\to (9,-2)$
5. ${\bar{z}}_5=1+6i\to (1,6)$

б) Построение ломаной линии по точкам ${\bar{z}}_1\to {\bar{z}}_2\to {\bar{z}}_3\to {\bar{z}}_4\to {\bar{z}}_5$

Появляются дополнительные точки на этой ломаной — те, которые лежат на отрезках между основными точками, и являются чисто мнимыми числами, т.е. числами вида $z=bi$, где $\text{Re}(z)=0$.

Из контекста сказано, что ломаной принадлежат следующие чисто мнимые числа:

1. $z_6=0+5.5i=5.5i$
2. $z_7=0+4i=4i$
3. $z_8=0-3i=-3i$
4. $z_9=0-4.5i=-4.5i$

Пояснение:
Эти точки были выбраны, потому что они лежат на отрезках между основными точками и имеют нулевую действительную часть. Значит, они лежат на мнимой оси (ось $y$).

в) Найдём точки на ломаной, у которых $\text{Re}(z)=-3$

Цель: Найти все точки, в которых действительная часть равна $-3$. Это значит, их абсцисса (ось $x$) — это $-3$.

Из предыдущих данных найдём такие точки:

1. $z_3=-3+6i$ — есть в списке исходных ${\bar{z}}_i$
2. $z_6=-3+4i$ — очевидно, действительная часть равна $-3$
3. $z_7=-3+0i=-3$ — тоже подходит

Ответ:
Эти три точки удовлетворяют условию:

$$z_3=-3+6i;z_6=-3+4i;z_7=-3+0i=-3$$

г) Найдём точки на ломаной, у которых $\text{Im}(z)=3$

Цель: Найти все точки, у которых мнимая часть (ось $y$) равна $3$. То есть, $z=a+3i$, где $a$ — любое число.

Из списка всех точек (исходных и добавленных) ищем такие:

1. ${\bar{z}}_1=-5+3i$ — подходит
2. $z_6=-2+3i$ — подходит
3. $z_7=1.5+3i$ — подходит
4. $z_8=4+3i$ — подходит

Ответ:

$${\bar{z}}_1=-5+3i;z_6=-2+3i;z_7=1.5+3i;z_8=4+3i$$

Итоговое понимание:

• Сначала были даны числа $z_1\dots z_5$ и их сопряжения ${\bar{z}}_1\dots {\bar{z}}_5$.
• Построили точки, соответствующие ${\bar{z}}_i$ на координатной плоскости.
• Соединили их отрезками — получили ломаную.
• Изучили дополнительные точки на этой ломаной (в частности, чисто мнимые и с определённой действительной/мнимой частью).
• Выявили точки с заданными условиями на $\text{Re}(z)$ и $\text{Im}(z)$.