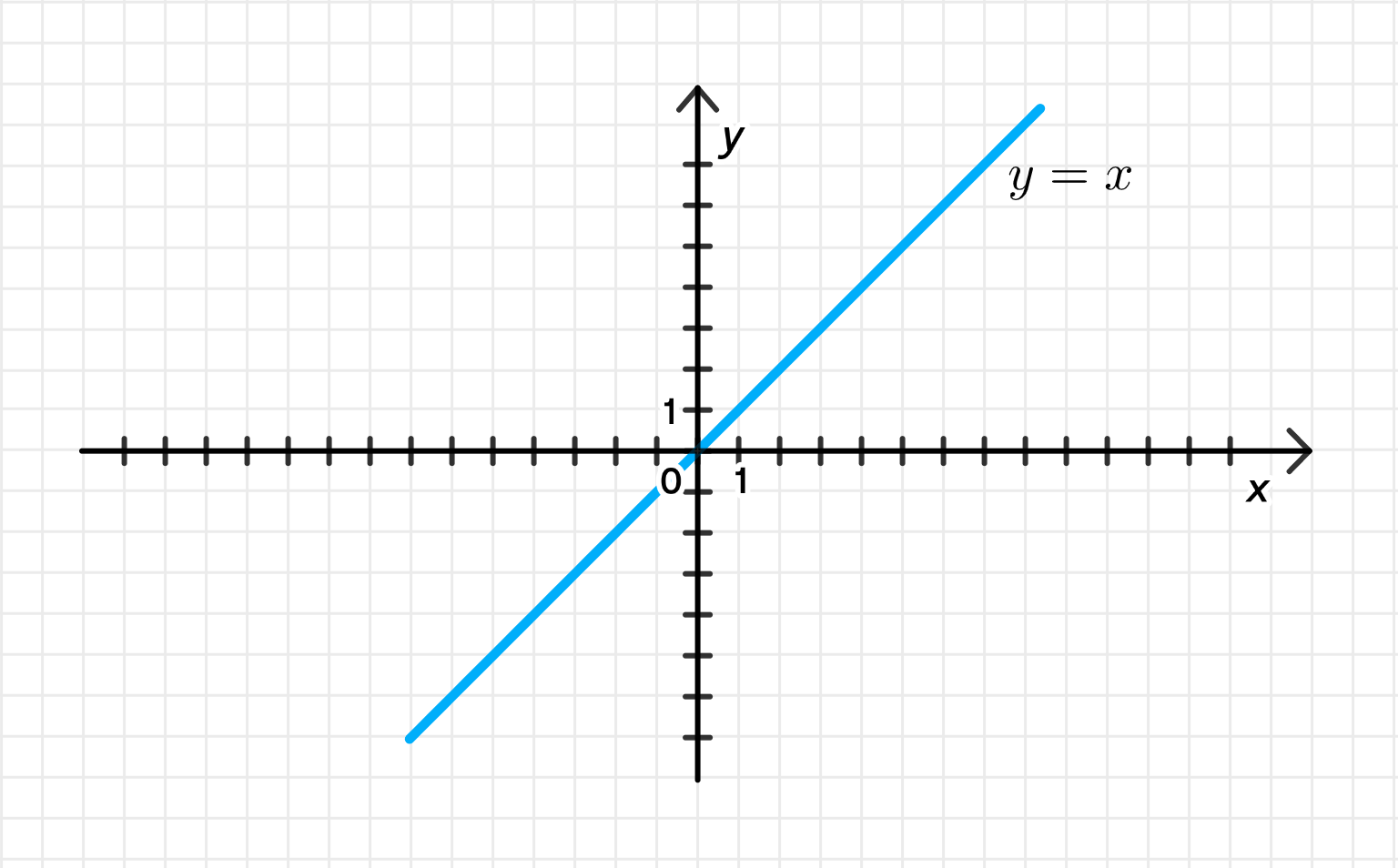ГДЗ по Алгебре 10 Класс Номер 33.4 Профильный Уровень Мордкович — Подробные Ответы

Изобразите на координатной плоскости множество всех комплексных чисел $z$, удовлетворяющих заданному условию:

а) Действительная часть равна $-2$;

б) Мнимая часть равна $3$ или $4$;

в) $\operatorname{Re} z = \operatorname{Im} z$;

г) $\operatorname{Re} z = (\operatorname{Im} z)^2$.

Изобразить множество всех комплексных чисел, у которых:

а) Действительная часть равна $-2$:

$$x = -2;$$

б) Мнимая часть равна $3$ или $4$:

$$y = 3 \text{ или } y = 4;$$

в) $Re\, z = Im\, z$:

$$x = y;$$

г) $Re\, z = (Im\, z)^2$:

$$x=y^2;$$

$$x = y^2;$$

Изобразить множество всех комплексных чисел, у которых:

Предварительное пояснение

Комплексное число $z$ имеет вид:

$$z = x + iy,$$

где:

• $x = \text{Re}(z)$ — действительная часть комплексного числа;
• $y = \text{Im}(z)$ — мнимая часть комплексного числа.

На комплексной плоскости (гауссовой плоскости):

• Ось абсцисс (горизонталь) — это ось действительных чисел ($x$);
• Ось ординат (вертикаль) — это ось мнимых чисел ($y$).

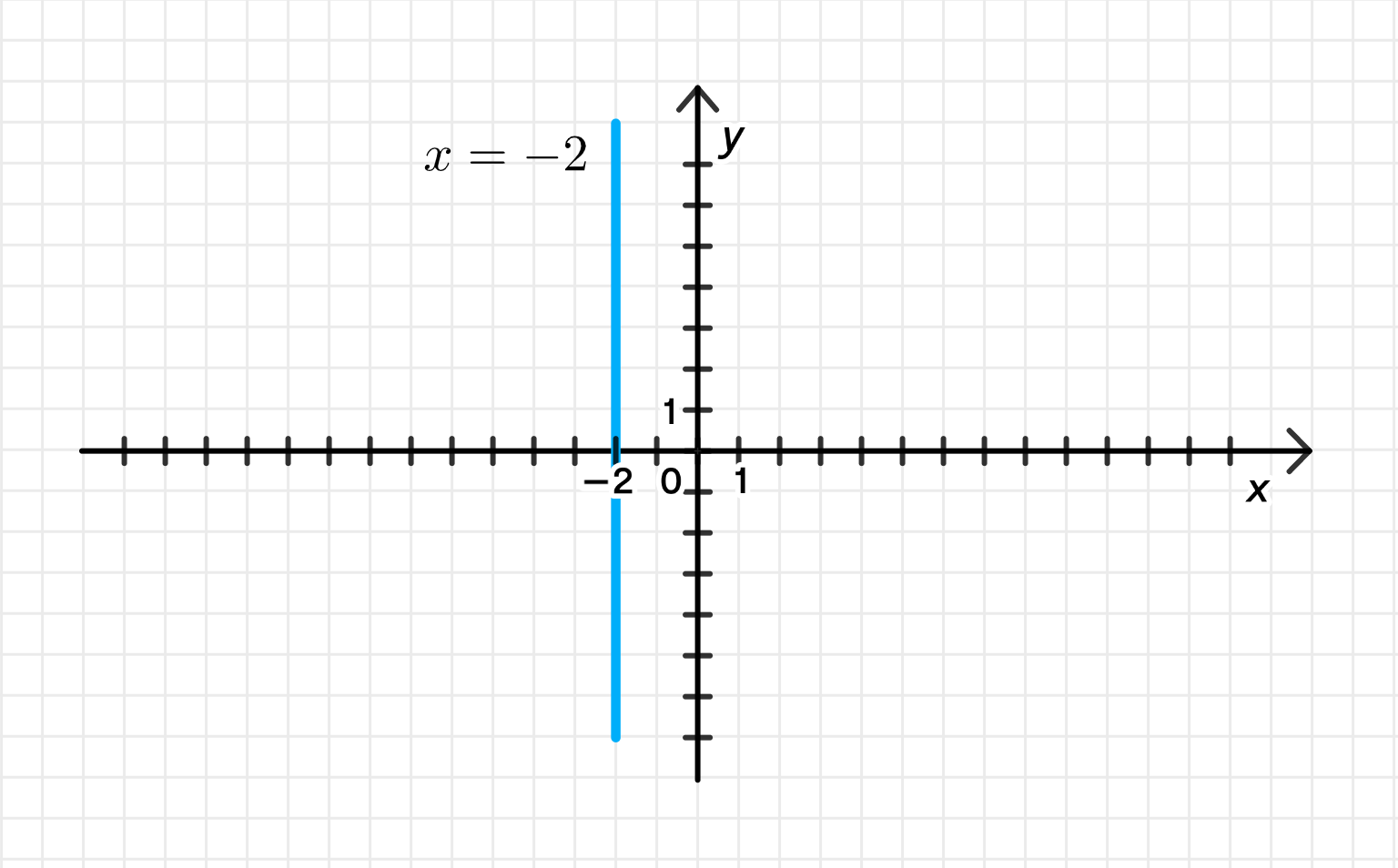
а) Действительная часть равна $-2$

Условие:

$$\text{Re}(z) = -2 \Rightarrow x = -2$$

Решение:

• Это означает, что значение $x$ фиксировано и равно $-2$, а значение $y$ может быть любым числом:

$$z = -2 + iy,\quad y \in \mathbb{R}$$

Геометрическая интерпретация:

• Это прямая линия, параллельная оси $y$, проходящая через точку $(-2, 0)$.

На комплексной плоскости:

• Это вертикальная прямая, на которой каждая точка имеет координату $x = -2$.

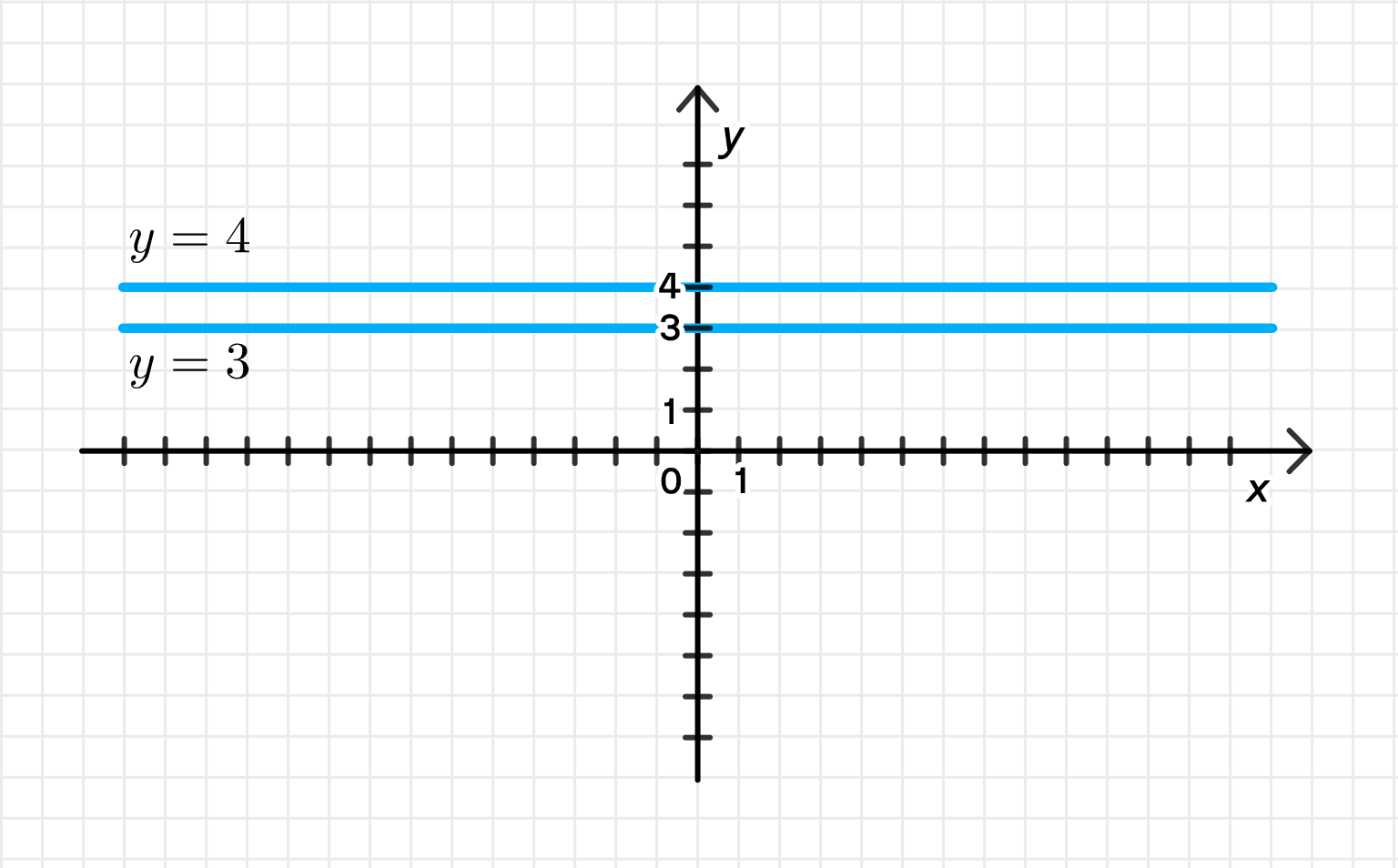
б) Мнимая часть равна $3$ или $4$

Условие:

$$\text{Im}(z) = 3 \quad \text{или} \quad \text{Im}(z) = 4 \Rightarrow y = 3 \quad \text{или} \quad y = 4$$

Решение:

• Значение $y$ фиксировано и равно либо 3, либо 4.
• Значение $x$ может быть любым:

$$z = x + 3i \quad \text{или} \quad z = x + 4i, \quad x \in \mathbb{R}$$

Геометрическая интерпретация:

• Это две горизонтальные прямые, каждая параллельна оси $x$, проходящие через точки с мнимой частью 3 и 4.

На комплексной плоскости:

• Одна прямая проходит через $y = 3$, другая — через $y = 4$.
• Все точки на этих прямых имеют фиксированную мнимую часть, но любую действительную.

в) $\text{Re}\, z = \text{Im}\, z$

Условие:

$$x = y$$

Решение:

• Значения $x$ и $y$ равны:

$$z = x + ix = x(1 + i),\quad x \in \mathbb{R}$$

Геометрическая интерпретация:

• Это прямая линия, идущая под углом 45° к осям координат.
• Угловой коэффициент: $k = 1$, поскольку $y = x$.

На комплексной плоскости:

• Прямая проходит через начало координат (0, 0) и все точки, где действительная и мнимая части равны.

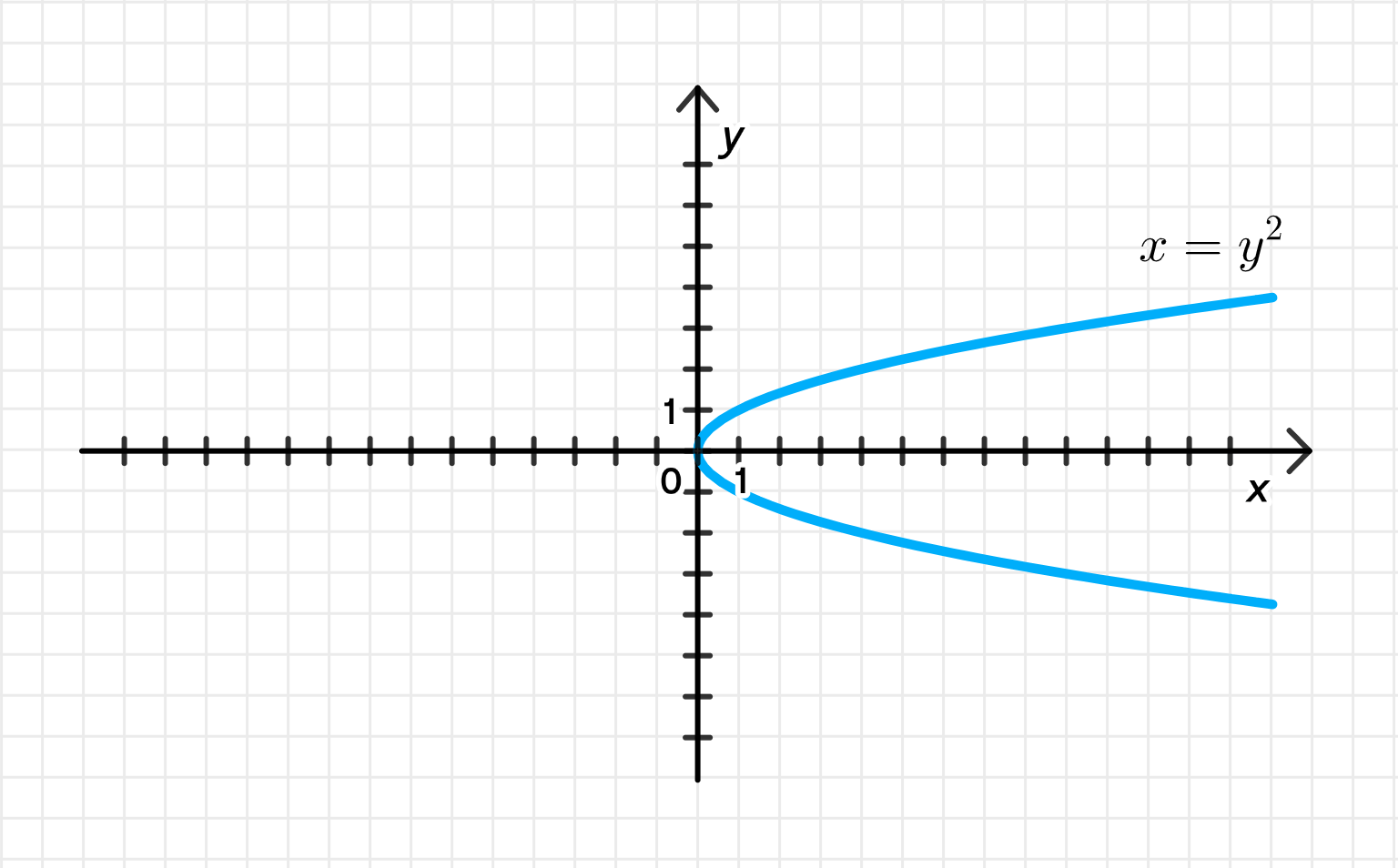
г) $\text{Re}\, z = (\text{Im}\, z)^2$

Условие:

$$x = y^2$$

Решение:

• Это зависимость между $x$ и $y$, где:

$$z = y^2 + iy,\quad y \in \mathbb{R}$$

• Здесь $x$ зависит от $y$, и принимает только неотрицательные значения, так как $x = y^2 \geq 0$.

Геометрическая интерпретация:

• Это парабола, ветви которой направлены вправо (в сторону возрастания $x$).

На комплексной плоскости:

• Все точки на этой кривой удовлетворяют условию, что действительная часть равна квадрату мнимой: $x = y^2$.
• Например:
  • При $y = -2$: $x = 4$ → $z = 4 — 2i$
  • При $y = 0$: $x = 0$ → $z = 0 + 0i$
  • При $y = 2$: $x = 4$ → $z = 4 + 2i$