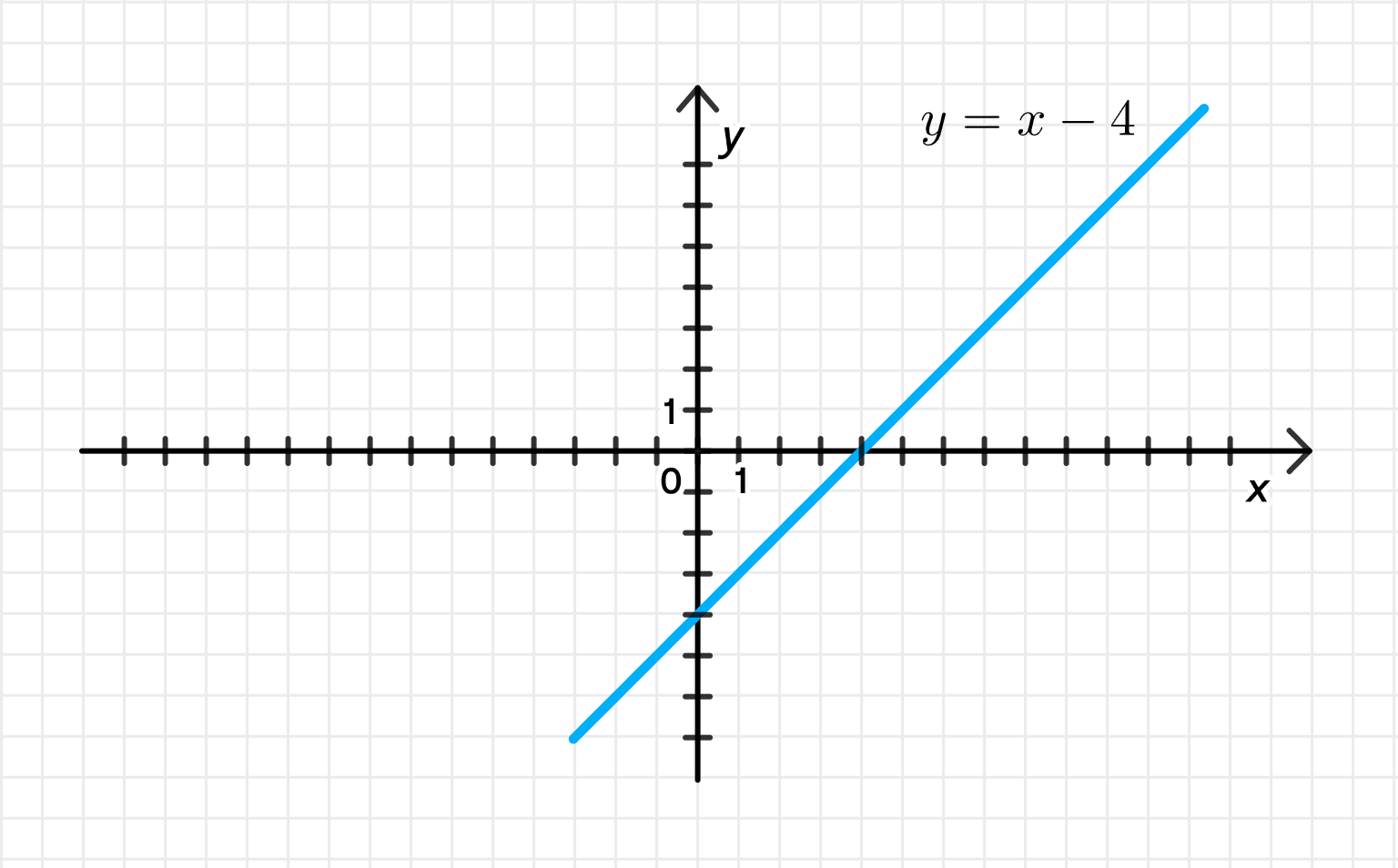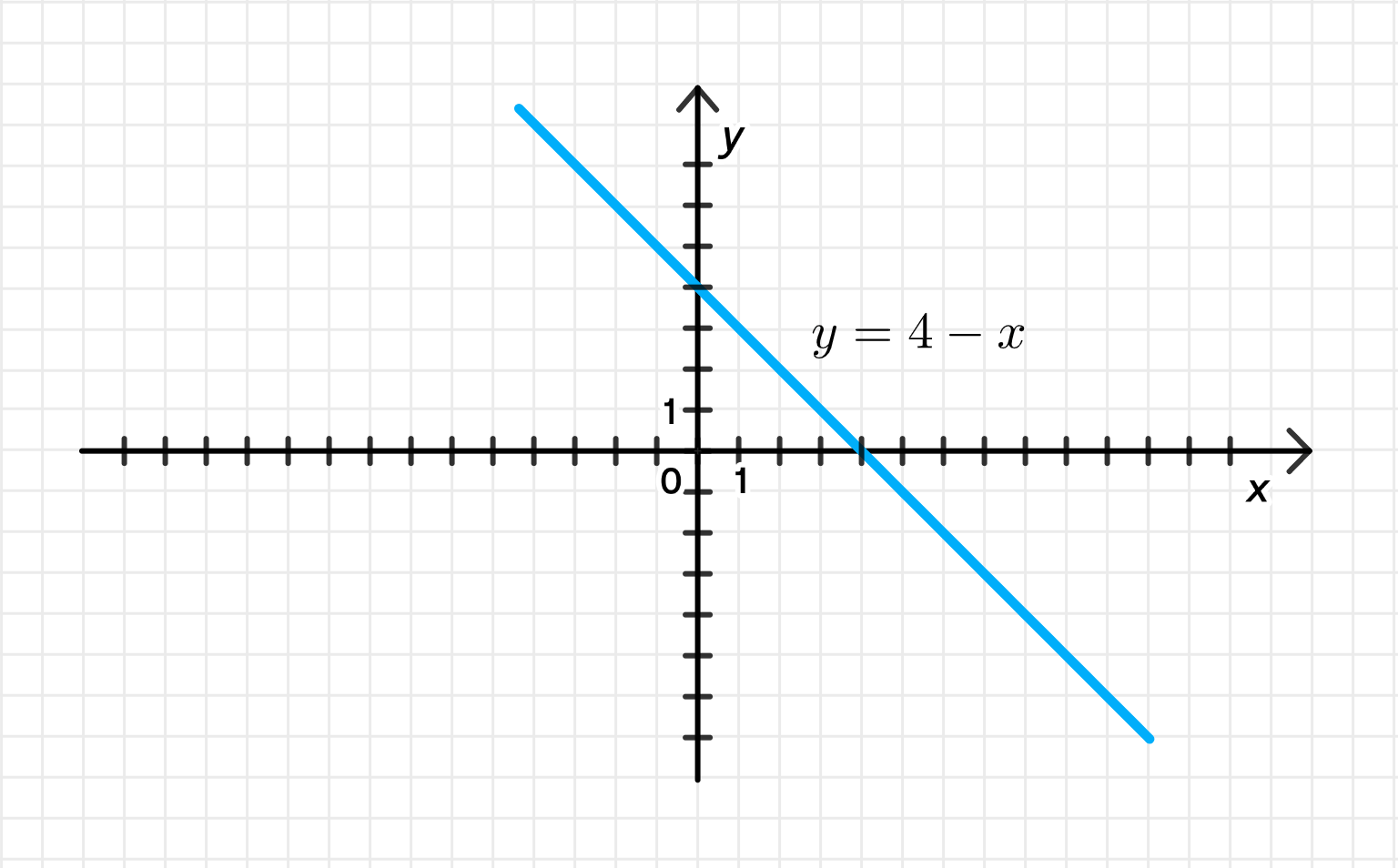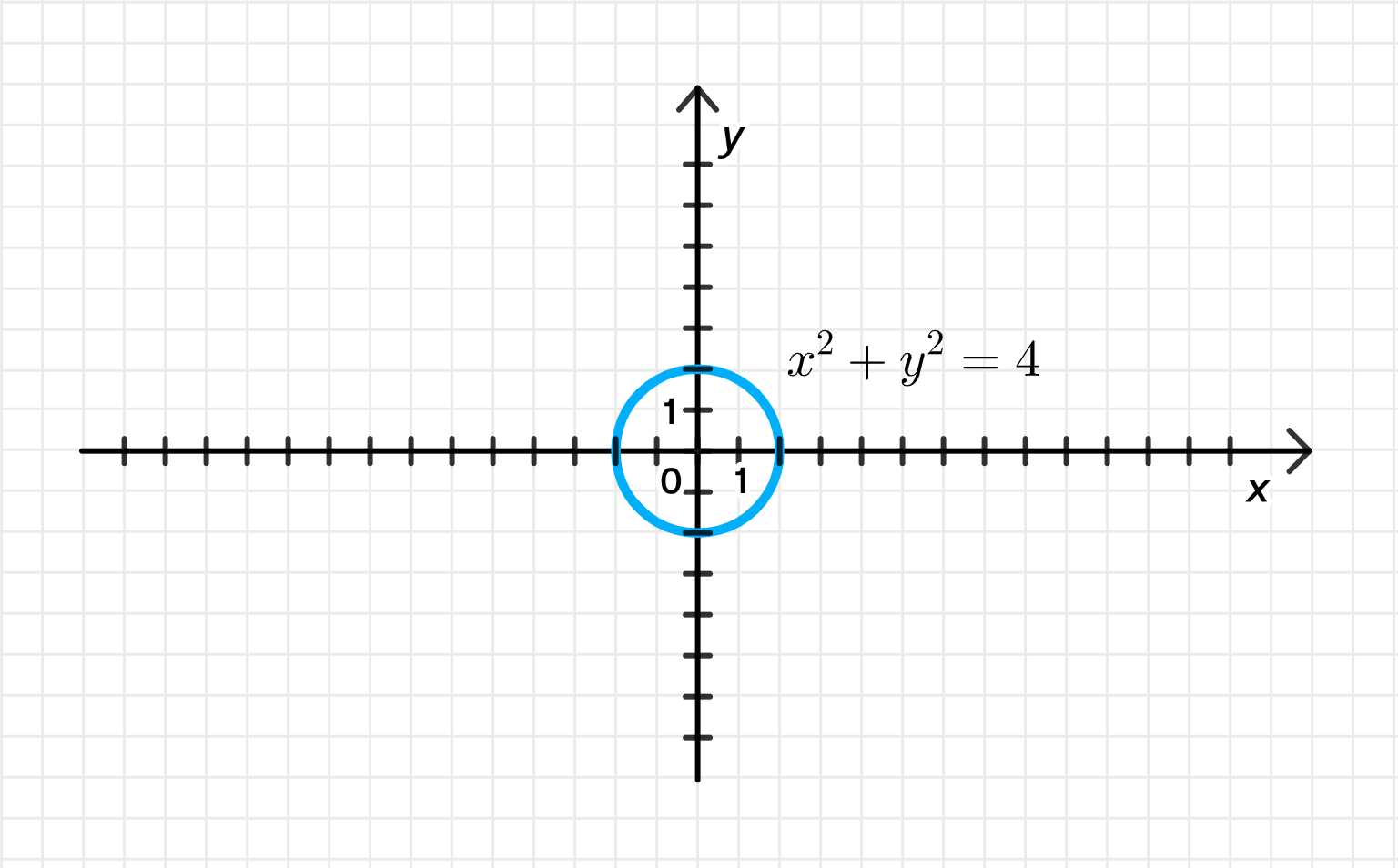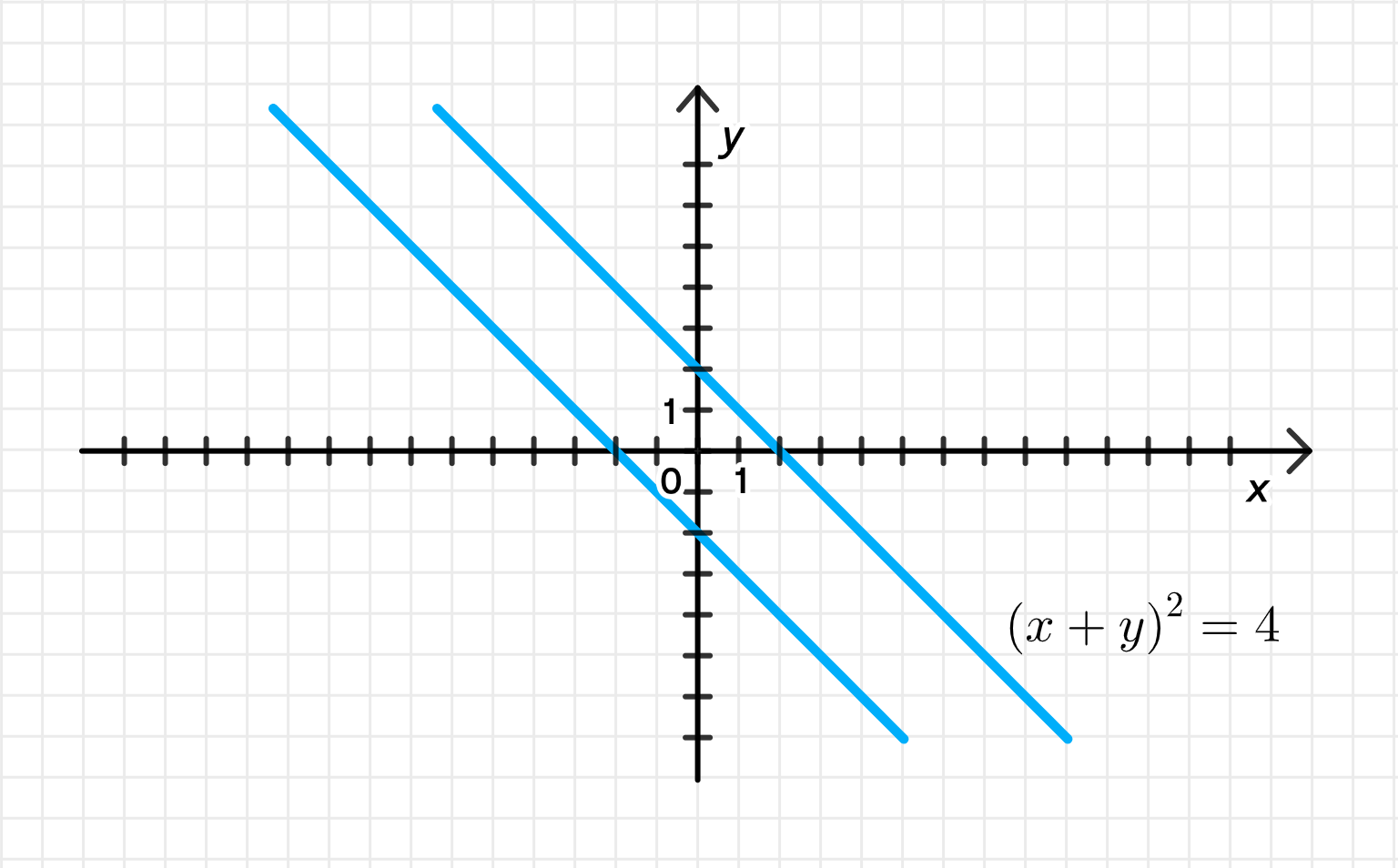ГДЗ по Алгебре 10 Класс Номер 33.6 Профильный Уровень Мордкович — Подробные Ответы

a) Действительная часть на 4 больше мнимой части;

б) сумма действительной и мнимой частей равна 4;

в) сумма квадратов действительной и мнимой частей равна 4;

г) квадрат суммы действительной и мнимой частей равен 4.

Изобразить множество всех комплексных чисел, у которых:

а) Действительная часть на 4 больше мнимой части:
$x = y + 4;$
$y = x — 4;$

б) Сумма действительной и мнимой частей равна 4:
$x + y = 4;$
$y = 4 — x;$

в) Сумма квадратов действительной и мнимой частей равна 4:
$x^2 + y^2 = 4;$
$x_0 = 0, \, y_0 = 0, \, R = 2;$

г) Квадрат суммы действительной и мнимой частей равен 4:
$(x + y)^2 = 4;$
$x + y = \pm 2;$
$y=-2-x\text{ или }y=2-x;$

$y = -2 — x \text{ или } y = 2 — x;$

а) Действительная часть на 4 больше мнимой части

Условие:

$x = y + 4$

Пояснение:

Комплексное число $z = x + iy$ должно удовлетворять этому соотношению между действительной и мнимой частью. Это означает, что:

• при каждом значении мнимой части $y$, действительная часть $x$ будет на 4 больше.
• То есть:
  $x = y + 4 \quad \text{или} \quad y = x — 4$

Геометрическая интерпретация:

Это прямая линия в комплексной плоскости (координатной плоскости $\mathbb{R}^2$, где ось абсцисс — $x$, ось ординат — $y$).

• Уравнение $y = x — 4$ — это уравнение прямой.
• Прямая с углом наклона 1 (то есть под 45°), сдвинута вниз на 4 единицы.
• Пересекает ось $x$, когда $y = 0$:
  $0 = x — 4 \Rightarrow x = 4 \Rightarrow (4, 0)$
• Пересекает ось $y$, когда $x = 0$:
  $y = 0 — 4 = -4 \Rightarrow (0, -4)$

б) Сумма действительной и мнимой частей равна 4

Условие:

$x + y = 4$

Пояснение:

Это прямая, на которой сумма координат (реальной и мнимой части) равна 4.

• Перепишем:
  $y = 4 — x$

Геометрическая интерпретация:

• Прямая с углом наклона -1 (спадающая прямая), пересекает ось $y$ в точке $(0, 4)$, и ось $x$ — в точке $(4, 0)$.
• Каждая точка на прямой удовлетворяет $x + y = 4$.

в) Сумма квадратов действительной и мнимой частей равна 4

Условие:

$x^2 + y^2 = 4$

Пояснение:

• Это уравнение окружности в координатной плоскости.

Геометрическая интерпретация:

• Окружность с центром в точке $(0, 0)$
• Радиус:
  $R = \sqrt{4} = 2$
• Все комплексные числа на этой окружности имеют модуль 2:
  $|z| = \sqrt{x^2 + y^2} = 2$

г) Квадрат суммы действительной и мнимой частей равен 4

Условие:

$(x + y)^2 = 4$

Пояснение:

• Это алгебраическое уравнение. Нам нужно раскрыть скобки:
  $(x + y)^2 = x^2 + 2xy + y^2 = 4$
• Но проще решить как:
  $x + y = \pm 2$

То есть:

• Либо $x + y = 2$
• Либо $x + y = -2$

Геометрическая интерпретация:

• Это две прямые:
  1. $x + y = 2 \Rightarrow y = 2 — x$
  2. $x + y = -2 \Rightarrow y = -2 — x$
• Обе — прямые с углом наклона -1, то есть параллельны, но имеют разные точки пересечения с осями.

Примеры точек:

• Для первой прямой:
  $x = 0 \Rightarrow y = 2$
  $x = 2 \Rightarrow y = 0$
• Для второй:
  $x = 0 \Rightarrow y = -2$
  $x = -2 \Rightarrow y = 0$