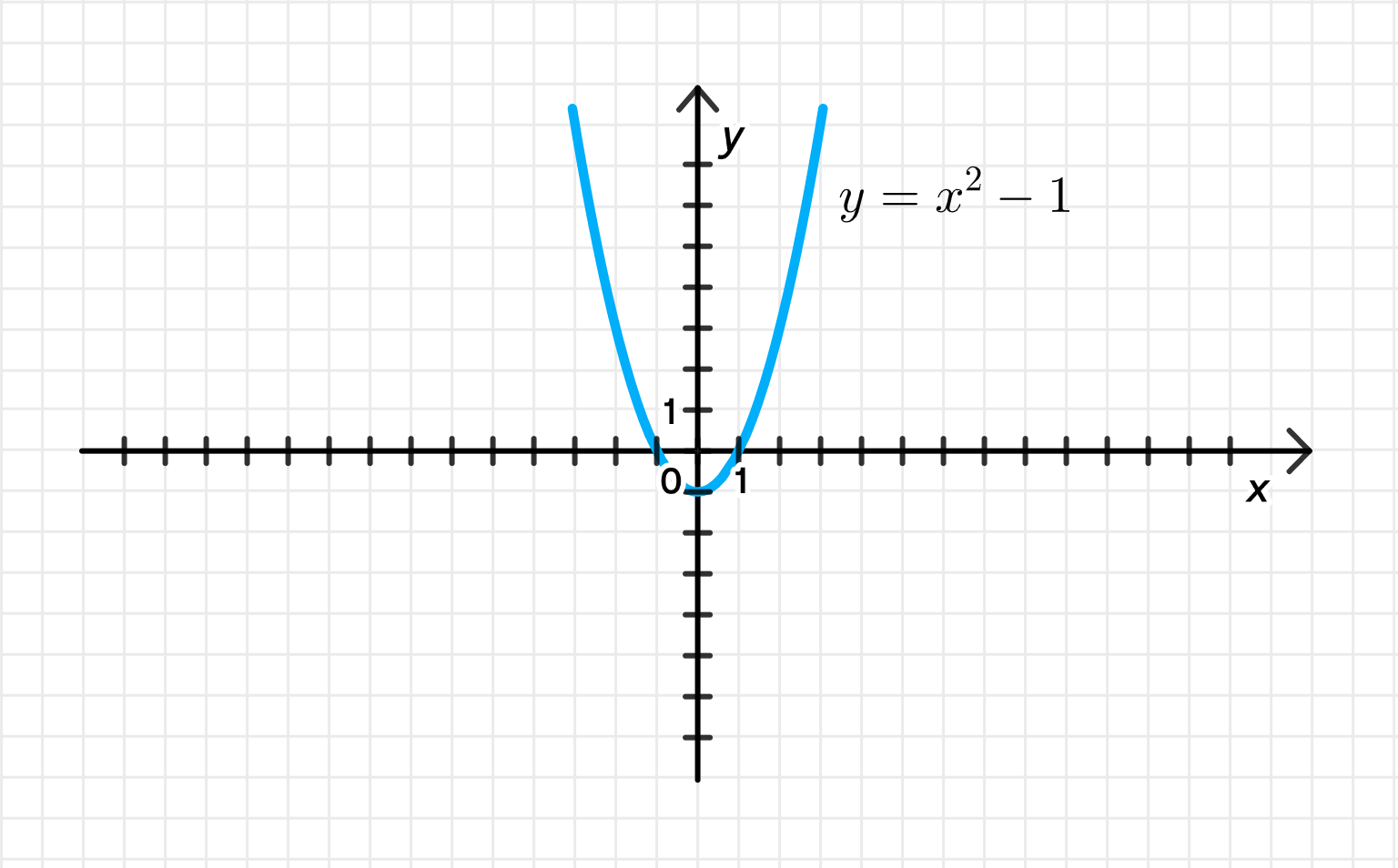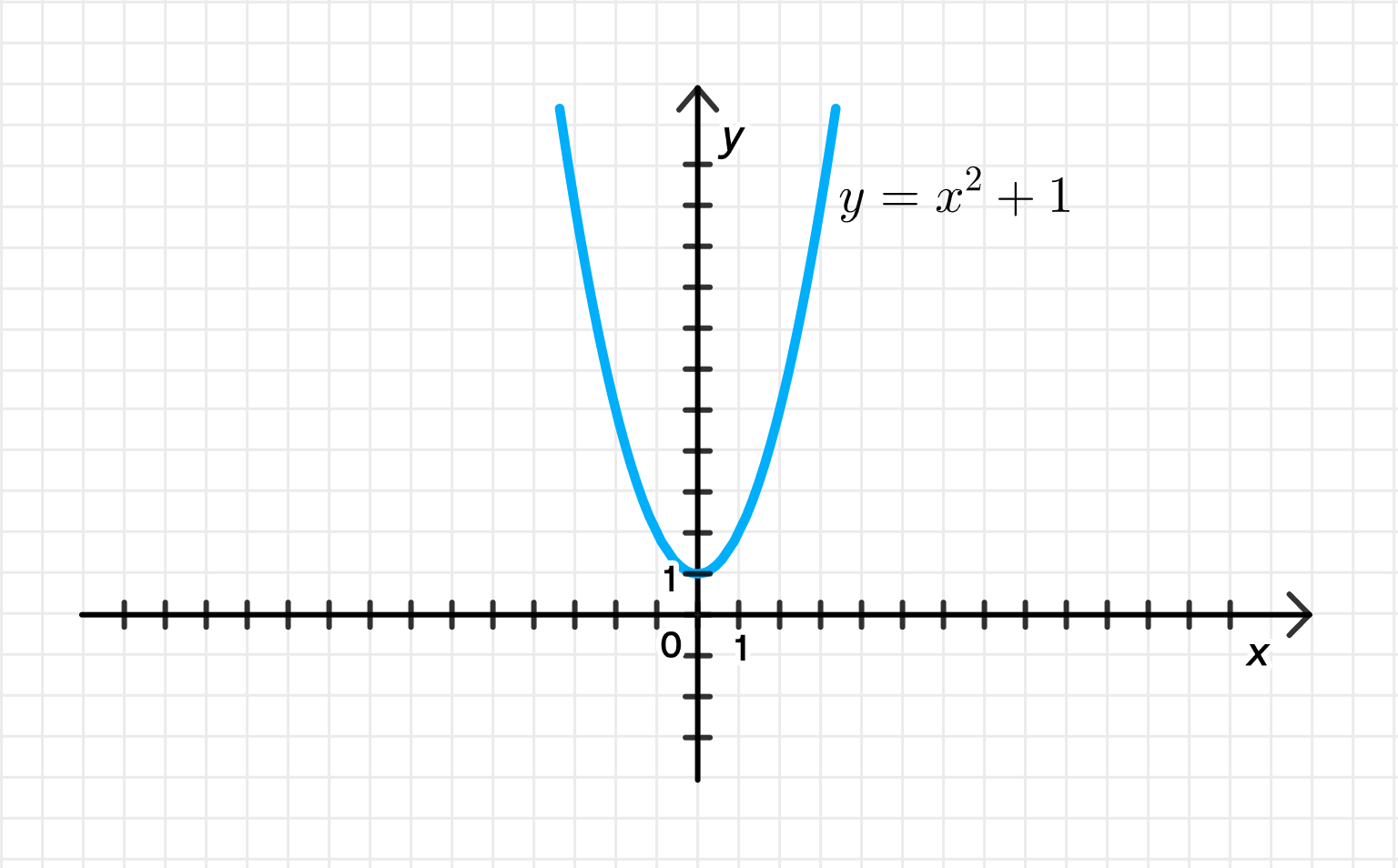ГДЗ по Алгебре 10 Класс Номер 33.7 Профильный Уровень Мордкович — Подробные Ответы

Изобразить множество всех комплексных чисел $z$, у которых:

а) $|Re\,z| — |Im\,z| = 1$;
$|x| — |y| = 1;$
$|y| = |x| + 1;$

б) $(Re\,z)^2 = Im\,z + 1$;
$x^2 = y + 1;$
$y = x^2 — 1;$

в) $(Re\,z)^2 = Im\,z — 1$;
$x^2 = y — 1;$
$y = x^2 + 1;$

г) $(Re\,z)(Im\,z) = 1$;
$xy = 1;$
$y = \frac{1}{x};$

Мы будем рассматривать каждую часть (а-г) поэтапно, включая:

1. Перевод условия из комплексной формы в декартову (с действительной и мнимой частью).
2. Упрощение уравнения.
3. Анализ области определения и свойств графика.
4. Построение множества точек.

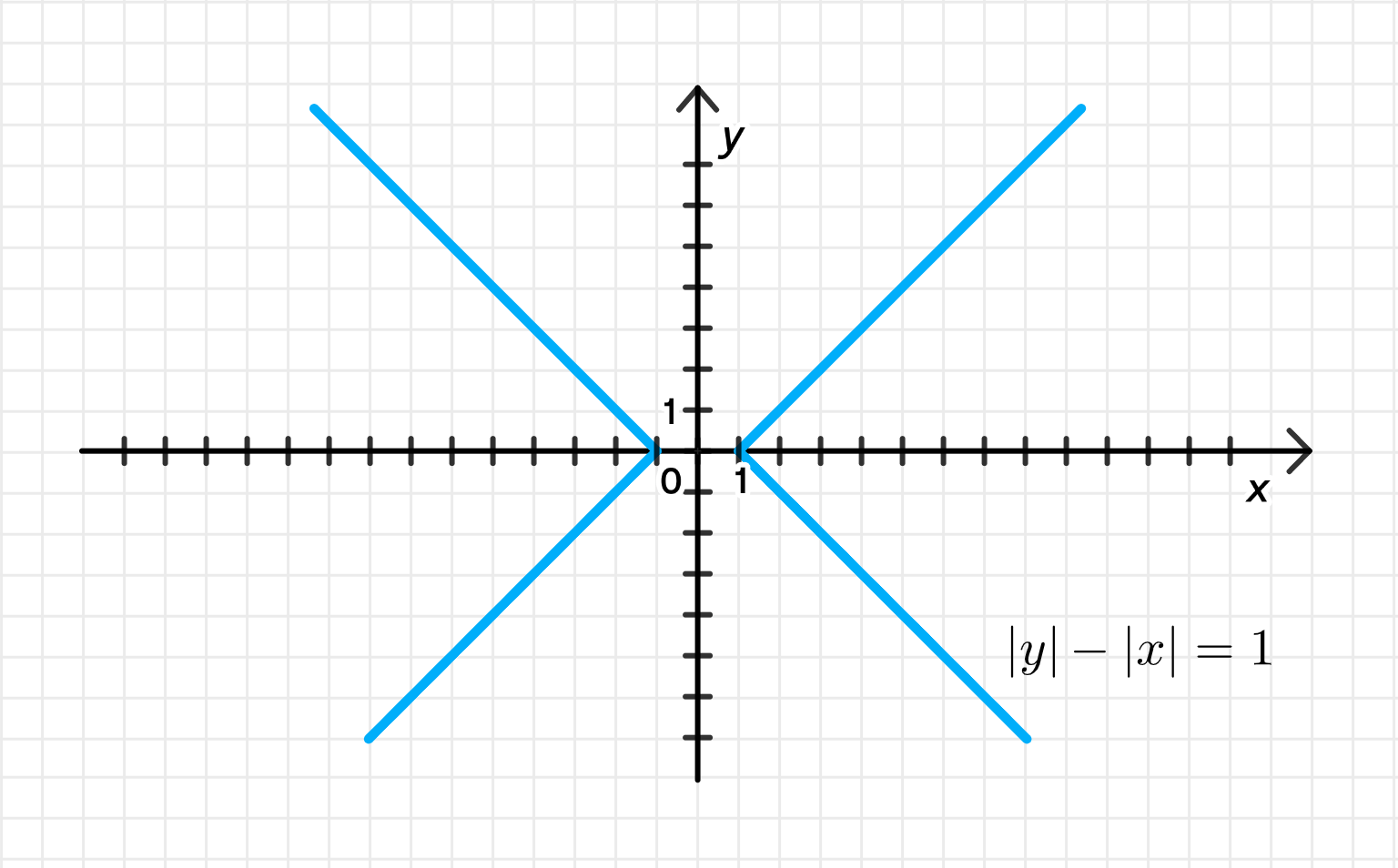
а) $|Re\,z| — |Im\,z| = 1$

Пусть $z = x + iy$, где $x = Re\,z$, $y = Im\,z$. Тогда:

$$|x| — |y| = 1$$

Это неравенство нужно анализировать по случаям, так как модуль — кусочная функция:

Случай 1: $x \ge 0, y \ge 0$

$$|x| = x, \quad |y| = y \Rightarrow x — y = 1 \Rightarrow y = x — 1$$

Условие: $x \ge 0$, $y \ge 0 \Rightarrow x — 1 \ge 0 \Rightarrow x \ge 1$

Подмножество 1:

$$y = x — 1, \quad x \ge 1$$

Случай 2: $x \ge 0, y < 0$

$$|x| = x, \quad |y| = -y \Rightarrow x + y = 1 \Rightarrow y = 1 — x$$

Условие: $x \ge 0$, $y < 0 \Rightarrow 1 — x < 0 \Rightarrow x > 1$

Подмножество 2:

$$y = 1 — x, \quad x > 1$$

Случай 3: $x < 0, y \ge 0$

$$|x| = -x, \quad |y| = y \Rightarrow -x — y = 1 \Rightarrow y = -x — 1$$

Условие: $x < 0$, $y \ge 0 \Rightarrow -x — 1 \ge 0 \Rightarrow x \le -1$

Подмножество 3:

$$y = -x — 1, \quad x \le -1$$

Случай 4: $x < 0, y < 0$

$$|x| = -x, \quad |y| = -y \Rightarrow -x + y = 1 \Rightarrow y = x + 1$$

Условие: $x < 0$, $y < 0 \Rightarrow x + 1 < 0 \Rightarrow x < -1$

Подмножество 4:

$$y = x + 1, \quad x < -1$$

б) $(Re\,z)^2 = Im\,z + 1$

Переход к переменным:

$$x^2 = y + 1 \Rightarrow y = x^2 — 1$$

Это обычная парабола, ветви вверх.

• Вершина: $(0, -1)$
• Область определения: $x \in \mathbb{R}$
• Область значений: $y\ge -1$

$y = x^2$в) $(Re\,z)^2 = Im\,z — 1$

$$x^2 = y — 1 \Rightarrow y = x^2 + 1$$

Снова парабола, ветви вверх.

• Вершина: $(0, 1)$
• Область определения: $x \in \mathbb{R}$
• Область значений: $y\ge 1$

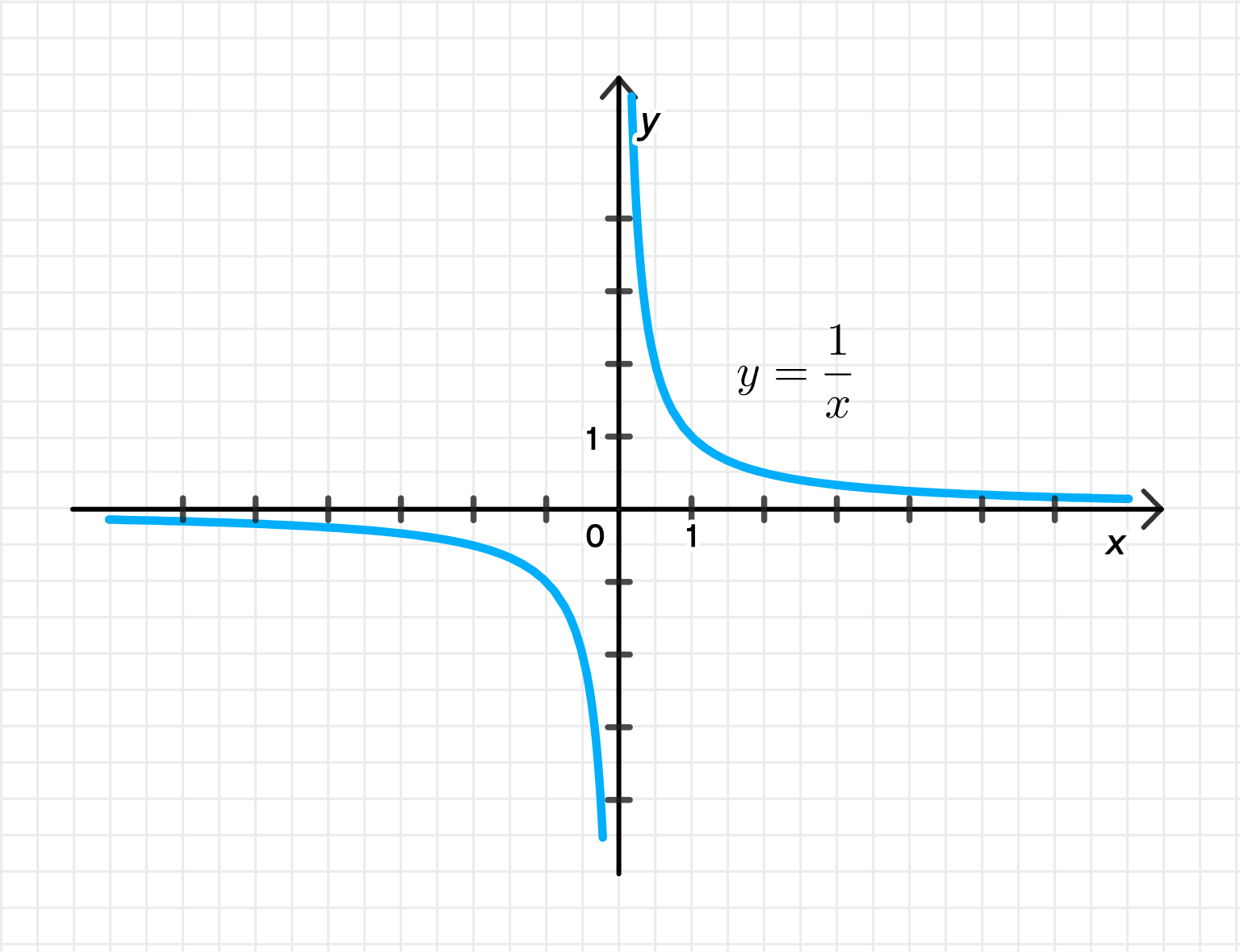
г) $(Re\,z)(Im\,z) = 1$

$$xy = 1 \Rightarrow y = \frac{1}{x}$$

Это гипербола.

• Область определения: $x \ne 0$
• Функция не определена в точке $x = 0$
• Ветви расположены в I и III четвертях