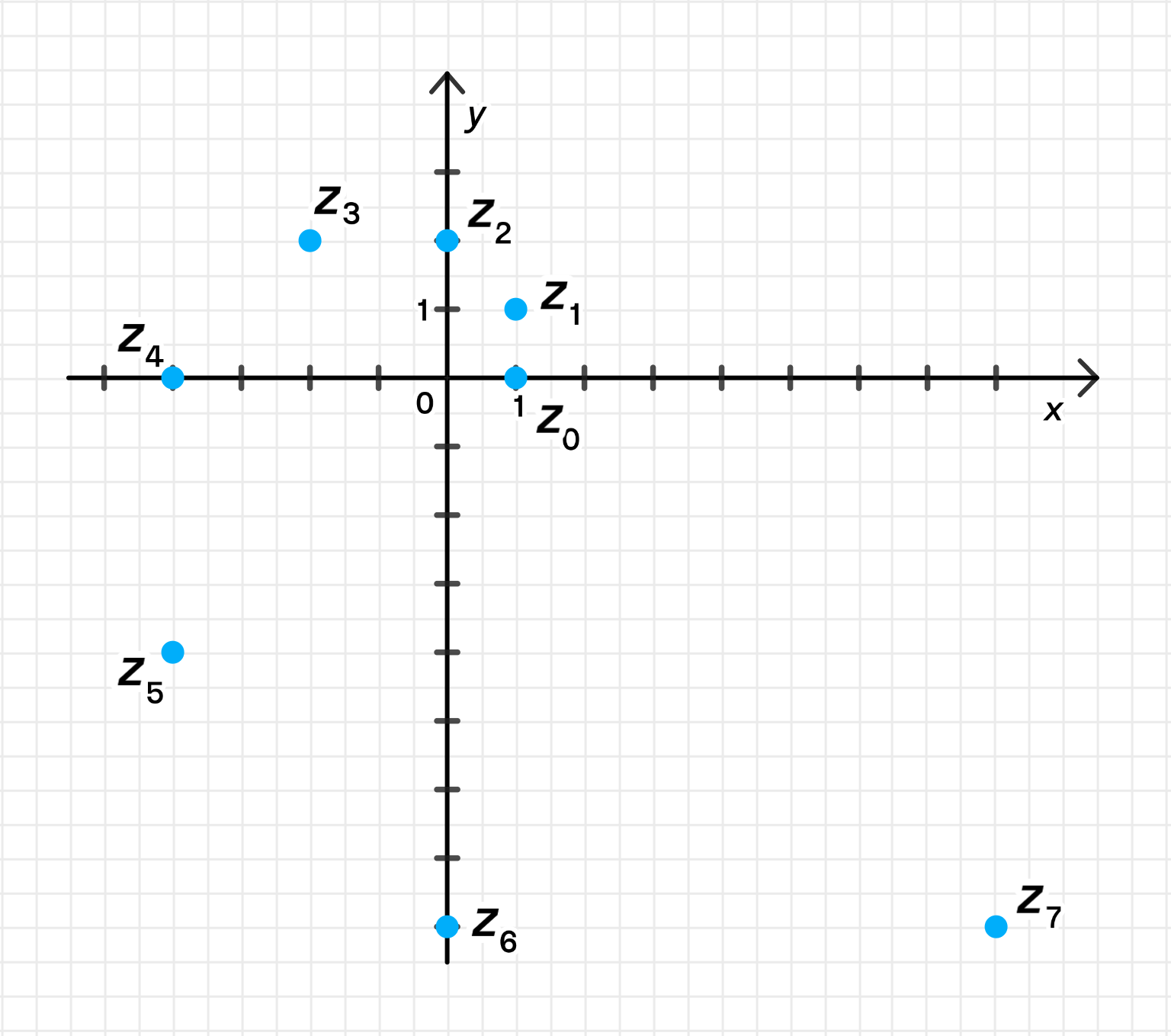ГДЗ по Алгебре 10 Класс Номер 33.8 Профильный Уровень Мордкович — Подробные Ответы

а) Отметьте на координатной плоскости точки, соответствующие комплексным числам $z_0 = 1$, $z_1 = 1 + i$, $z_2 = (1 + i)^2$, $z_3 = (1 + i)^3$, …, $z_7 = (1 + i)^7$.

б) Чему равна величина угла: $\angle z_0 O z_1$, $\angle z_1 O z_2$, …, $\angle z_6 O z_7$, $\angle z_7 O z_0$?

в) Перечислите все пары точек, лежащие по разные стороны от оси абсцисс. Сколько таких пар?

г) Запишите все числа, у которых произведение действительной и мнимой частей отрицательно. Сколько таких чисел?

Даны комплексные числа:

$$z_0 = 1;$$ $$z_1 = 1 + i;$$ $$z_2 = (1 + i)^2 = 1 + 2i + i^2 = 1 + 2i — 1 = 2i;$$ $$z_3 = (1 + i)^3 = 1 + 3i + 3i^2 + i^2 \cdot i = 1 + 3i — 3 — i = -2 + 2i;$$ $$z_4 = (1 + i)^4 = (2i)^2 = 4i^2 = -4;$$ $$z_5 = (1 + i)^5 = (-2 + 2i) \cdot 2i = -4i + 4i^2 = -4 — 4i;$$ $$z_6 = (1 + i)^6 = (2i)^3 = 8i^2 \cdot i = -8i;$$ $$z_7 = (1 + i)^7 = -8i \cdot (1 + i) = -8i — 8i^2 = 8 — 8i;$$

а) Данные точки на координатной плоскости:

б) По графику определим величину углов:

$$\angle z_0 O z_1 = \angle z_1 O z_2 = \cdots = \angle z_6 O z_7 = \angle z_7 O z_0 = 45^\circ;$$

в) Пары точек, лежащие по разные стороны от оси абсцисс:

$$z_1 z_5, \; z_1 z_6, \; z_2 z_5, \; z_2 z_6, \; z_3 z_5, \; z_3 z_6, \; z_3 z_7;$$

Всего есть 9 таких пар;

г) Числа, произведение действительной и мнимой частей которых отрицательно, то есть числа, которые лежат во II или IV четверти:

$$z_3, \; z_7;$$

Всего есть 2 таких числа

Дано:

Рассматриваем последовательность степеней числа $z = 1 + i$:

$$z_n = (1 + i)^n, \quad \text{для } n = 0, 1, 2, \ldots, 7$$

а) Вычисление чисел $z_0$ — $z_7$

Рассчитаем каждое из чисел пошагово, проверяя арифметику и используя свойства комплексных чисел:

$z_0 = (1 + i)^0 = 1$

По любому числу в нулевой степени:

$$z_0 = 1$$

$z_1 = (1 + i)^1 = 1 + i$

Просто само число:

$$z_1 = 1 + i$$

$z_2 = (1 + i)^2$

Используем формулу квадрата суммы:

$$(1 + i)^2 = 1^2 + 2 \cdot 1 \cdot i + i^2 = 1 + 2i + i^2$$

А так как $i^2 = -1$, получаем:

$$z_2 = 1 + 2i — 1 = 2i$$

$z_3 = (1 + i)^3$

Представим как:

$$(1 + i)^3 = (1 + i)^2 \cdot (1 + i) = 2i \cdot (1 + i)$$

Выполним умножение:

$$2i \cdot (1 + i) = 2i + 2i^2 = 2i — 2 = -2 + 2i$$ $$z_3 = -2 + 2i$$

$z_4 = (1 + i)^4$

Это:

$$(1 + i)^4 = [(1 + i)^2]^2 = (2i)^2 = 4i^2 = 4 \cdot (-1) = -4$$ $$z_4 = -4$$

$z_5 = (1 + i)^5$

Используем:

$$(1 + i)^5 = (1 + i)^4 \cdot (1 + i) = -4 \cdot (1 + i) = -4 — 4i$$ $$z_5 = -4 — 4i$$

$z_6 = (1 + i)^6$

Также:

$$(1 + i)^6 = (1 + i)^3 \cdot (1 + i)^3 = (-2 + 2i)^2$$

Посчитаем:

$$(-2 + 2i)^2 = (-2)^2 + 2 \cdot (-2) \cdot 2i + (2i)^2 = 4 — 8i + 4i^2$$ $$4 — 8i + 4(-1) = 4 — 8i — 4 = -8i$$ $$z_6 = -8i$$

$z_7 = (1 + i)^7$

Можно воспользоваться:

$$z_7 = z_6 \cdot z_1 = (-8i) \cdot (1 + i)$$

Выполним:

$$(-8i) \cdot (1 + i) = -8i — 8i^2 = -8i + 8 = 8 — 8i$$ $$z_7 = 8 — 8i$$

Итак, все числа:

б) Геометрический анализ (углы на плоскости)

Все эти числа можно представить как векторы из начала координат. Отметим следующее:

• Числа $z_n$ — это степени $(1 + i)$, которое по модулю:

  $$|1 + i| = \sqrt{1^2 + 1^2} = \sqrt{2}$$

• Углы между последующими числами $z_n$ на плоскости:

  Так как при умножении комплексного числа на $1 + i$ каждый раз увеличивается аргумент (угол) на:

  $$\arg(1 + i) = \arctan\left(\frac{1}{1}\right) = 45^\circ$$

• Следовательно, каждый следующий вектор поворачивается на 45° относительно предыдущего.

Вывод:

$$\angle z_0 O z_1 = \angle z_1 O z_2 = \cdots = \angle z_6 O z_7 = 45^\circ$$

в) Найдём пары точек по разные стороны от оси абсцисс

Рассматриваем пары $z_i, z_j$, у которых мнимые части разных знаков (одна положительная, другая отрицательная).

Разберём по значениям:

Теперь найдём пары $z_i, z_j$, где одна точка выше оси (Im > 0), а другая — ниже (Im < 0):

Положительная мнимая часть:

• $z_1, z_2, z_3$

Отрицательная мнимая часть:

• $z_5, z_6, z_7$

Составим все возможные пары между этими двумя группами:

1. $z_1$ и $z_5$
2. $z_1$ и $z_6$
3. $z_1$ и $z_7$
4. $z_2$ и $z_5$
5. $z_2$ и $z_6$
6. $z_2$ и $z_7$
7. $z_3$ и $z_5$
8. $z_3$ и $z_6$
9. $z_3$ и $z_7$

Итог: 9 пар точек, лежащих по разные стороны от оси абсцисс.

г) Числа, у которых произведение действительной и мнимой частей отрицательно

Произведение действительной и мнимой частей:

$$\text{Если } \operatorname{Re}(z_n) \cdot \operatorname{Im}(z_n) < 0 \Rightarrow z_n \text{ лежит во II или IV четверти}$$

Проверим все числа:

Ответ:

• Подходят: $z_3 = -2 + 2i$, $z_7 = 8 — 8i$
• Всего: 2 числа