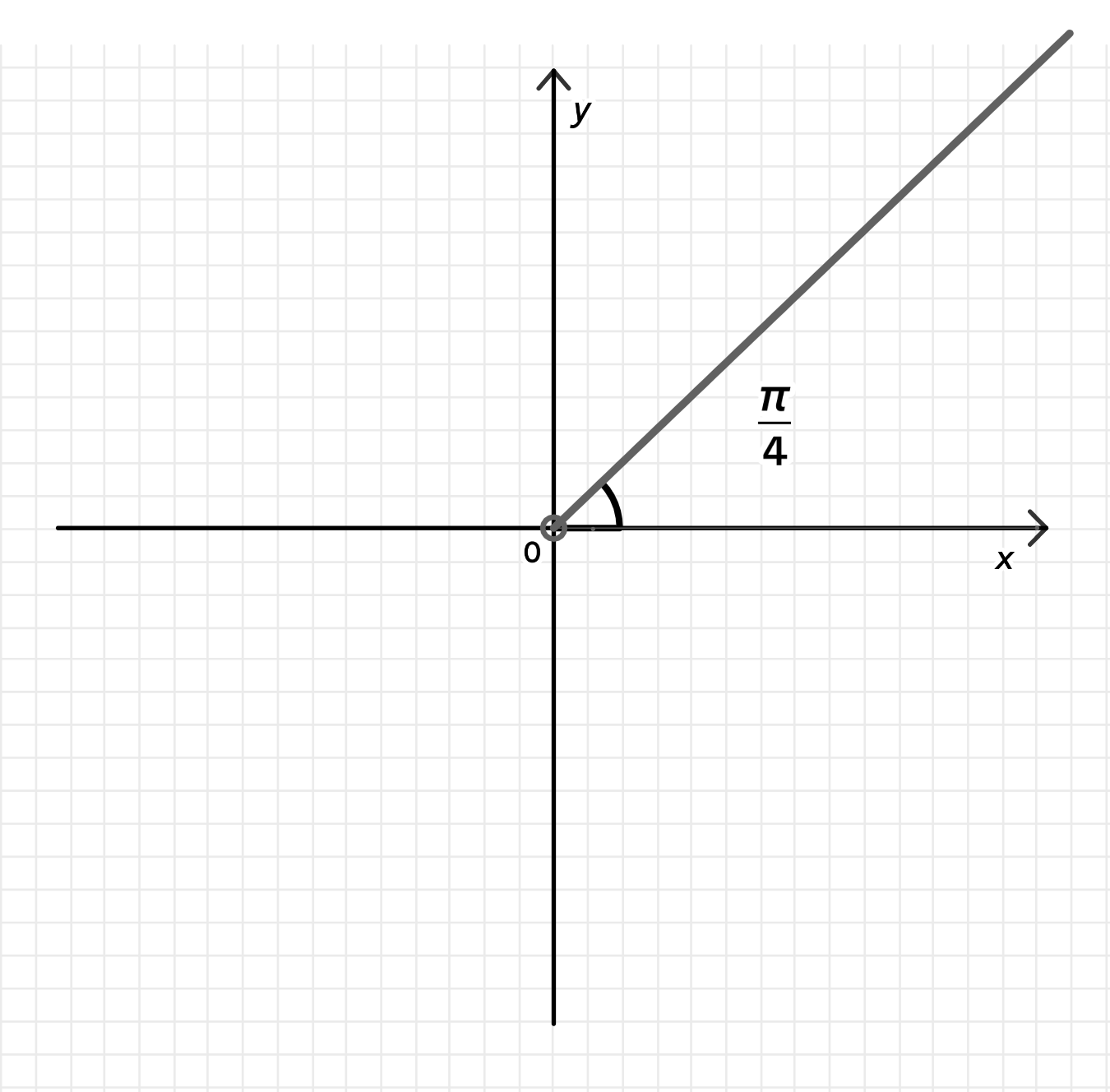Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 34.16 Профильный Уровень Мордкович — Подробные Ответы
Изобразите на комплексной плоскости множество всех тех чисел, аргумент которых равен:
а)
б)
в)
г)
Изобразить на комплексной плоскости множество всех тех чисел, аргумент которых равен:
а) :
б) или ;
или :
в) :
г) или ;
или :
Изобразить на комплексной плоскости множество всех таких комплексных чисел, аргумент которых равен заданному значению.
Что такое аргумент комплексного числа?
Для любого числа , его аргумент — это угол , который радиус-вектор образует с положительным направлением оси (действительной оси), при движении против часовой стрелки.
Если , то можно записать:
Геометрически
Множество всех чисел с одним и тем же аргументом — это полупряма, идущая из начала координат в определённом направлении (по углу ).
Все такие числа можно описать формулой:
То есть они лежат на луче от начала координат, под углом .
а)
Пояснение:
- Угол — это 45°, то есть угол между осью и вектором, идущим в первой четверти.
- Координаты вектора при любом :
Геометрическое множество:
- Это полупряма, идущая из точки , под углом к действительной оси.
- Все точки лежат в первой четверти, где и действительная, и мнимая части положительные.
Изображение:
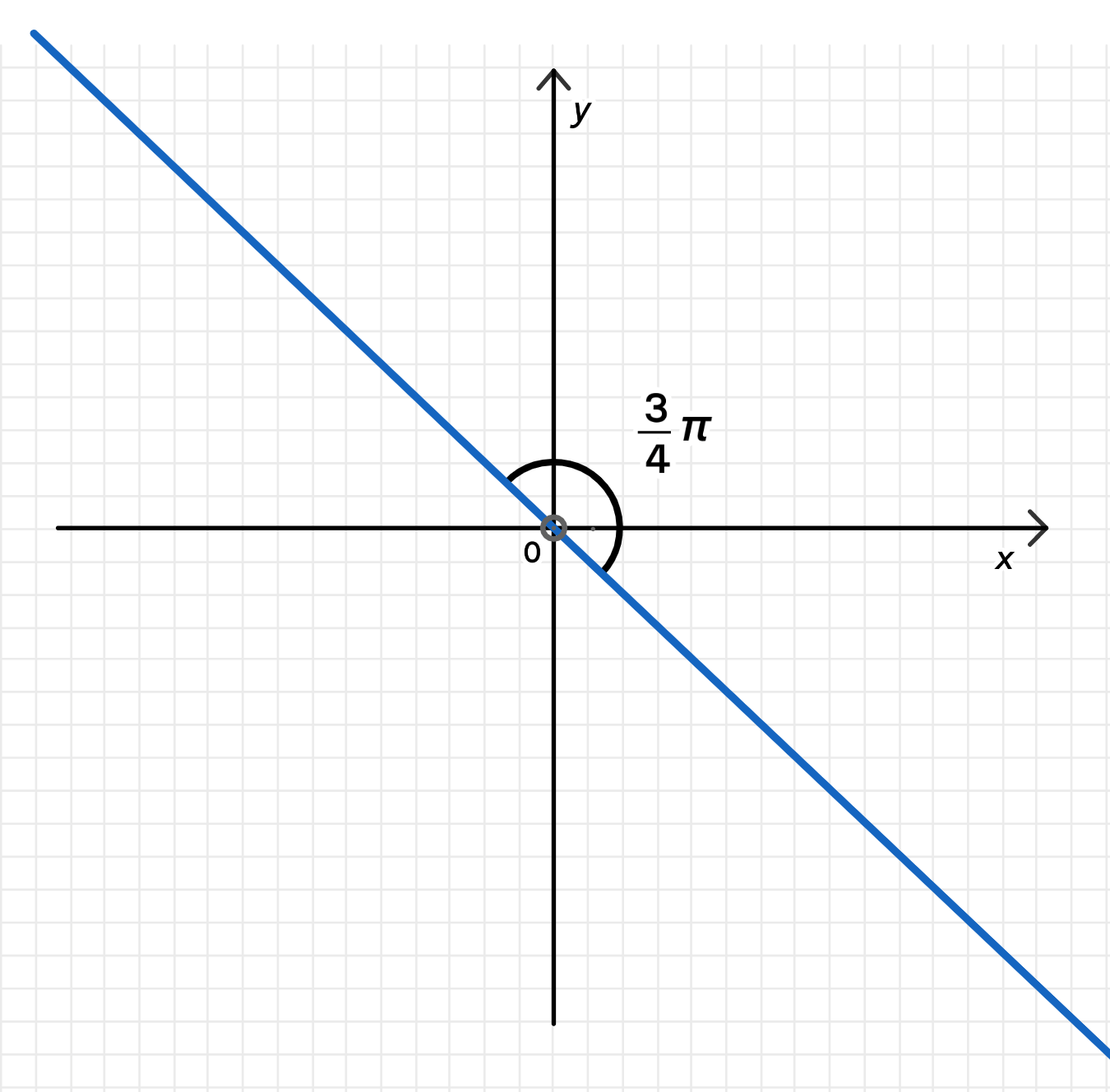
б) или
Угол :
- Это угол во второй четверти, от оси Re вверх налево.
- Формула луча:
Угол :
- Это угол в четвёртой четверти, от оси Re вниз вправо.
- Формула луча:
Геометрическое множество:
- Это две полупрямые, выходящие из начала координат:
- Под углом , вверх влево (вторая четверть);
- Под углом , вниз вправо (четвёртая четверть).
Изображение:
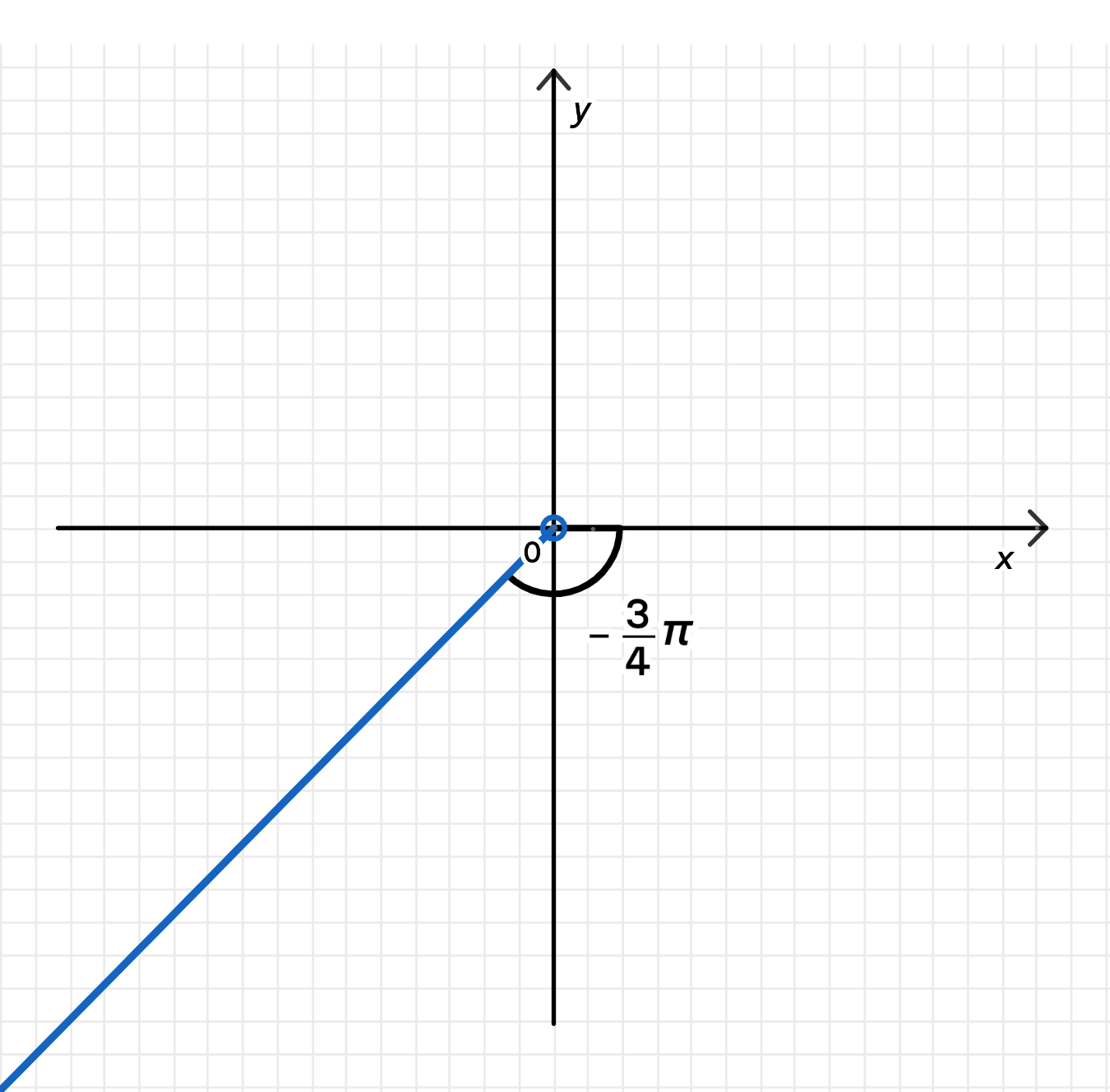
в)
Пояснение:
- Угол указывает на направление вниз влево, в третьей четверти.
- Формула:
Геометрическое множество:
- Полупряма в направлении , то есть от начала координат в третью четверть — и Re, и Im отрицательны.
Изображение:
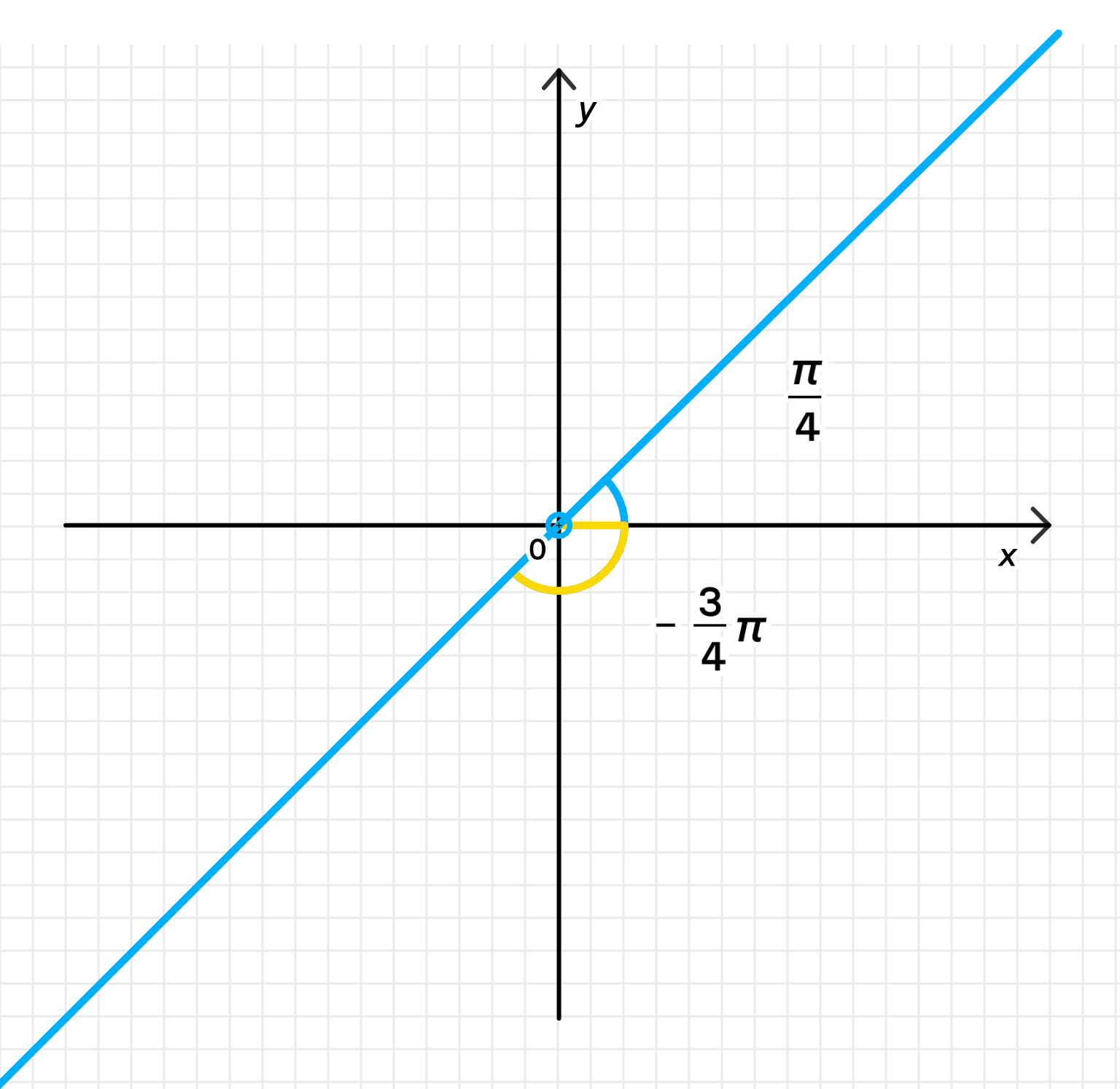
г) или
Пояснение:
Это объединение двух предыдущих случаев:
- — первая четверть;
- — третья четверть.
Геометрическое множество:
- Две луча:
- В направлении — вправо и вверх;
- В направлении — влево и вниз.
Изображение: