Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 34.17 Профильный Уровень Мордкович — Подробные Ответы
Изобразите на комплексной плоскости множество всех тех чисел, аргумент которых равен:
а)
б)
в)
г)
Изобразить на комплексной плоскости множество всех тех чисел, аргумент которых равен:
а)
б)
в)
г)
На комплексной плоскости любое комплексное число можно записать в тригонометрической форме:
где:
— модуль числа, расстояние от начала координат,
— аргумент, угол между положительным направлением оси Re и вектором .
Если аргумент фиксирован, а модуль может быть любым положительным числом, то множество таких чисел — прямые лучи из начала координат под заданными углами.
Разбор по пунктам:
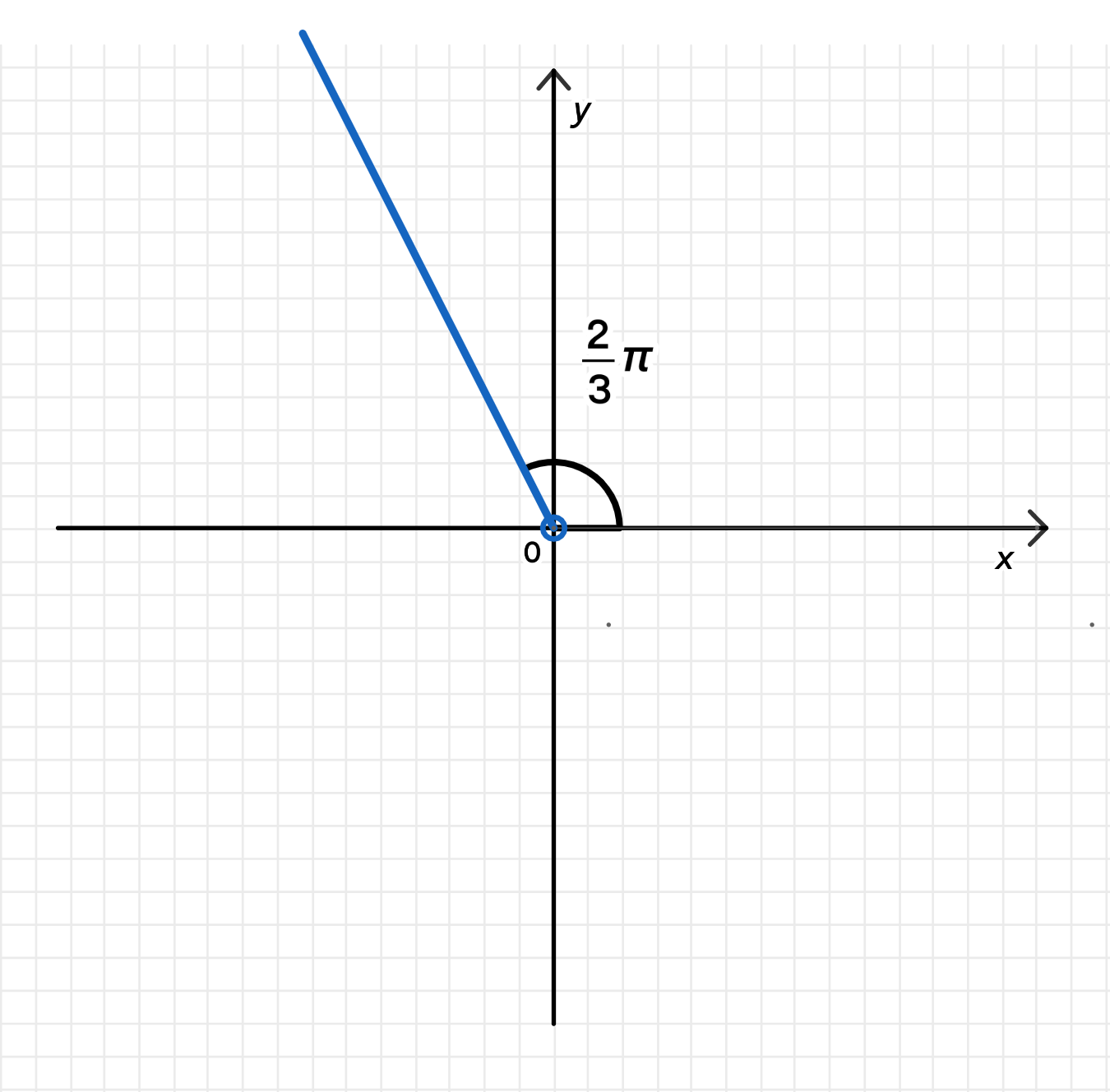
а)
Угол 120° (или ) — это угол между вектором и положительным направлением оси Re, отсчитывается против часовой стрелки.
На комплексной плоскости это луч, отходящий от начала координат под углом 120°.
Все такие числа имеют вид:
В координатах:
Это — прямая, идущая под углом 120° против часовой стрелки от начала, без самого начала (начало не включается, т.к. у 0 аргумент не определён).
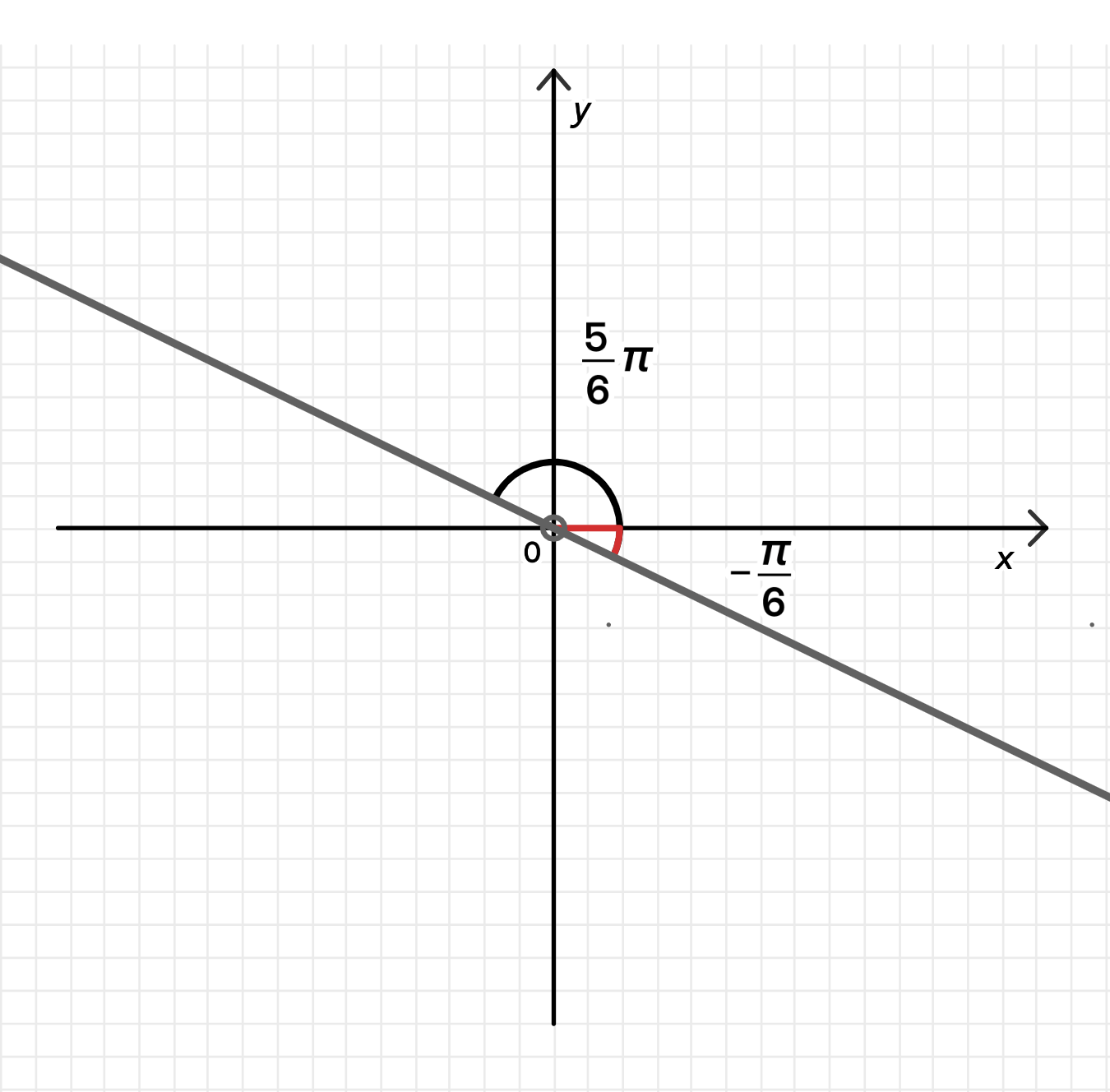
б) или
или
или
Это два разных луча:
— угол в отрицательном направлении, т.е. по часовой стрелке от положительной оси Re.
- Получаем луч под углом 330° (эквивалентно -30°).
- В координатной форме:
— угол против часовой стрелки, второй квадрант.
На рисунке это два луча: один уходит влево-вверх (150°), другой вправо-вниз (330° = -30°).
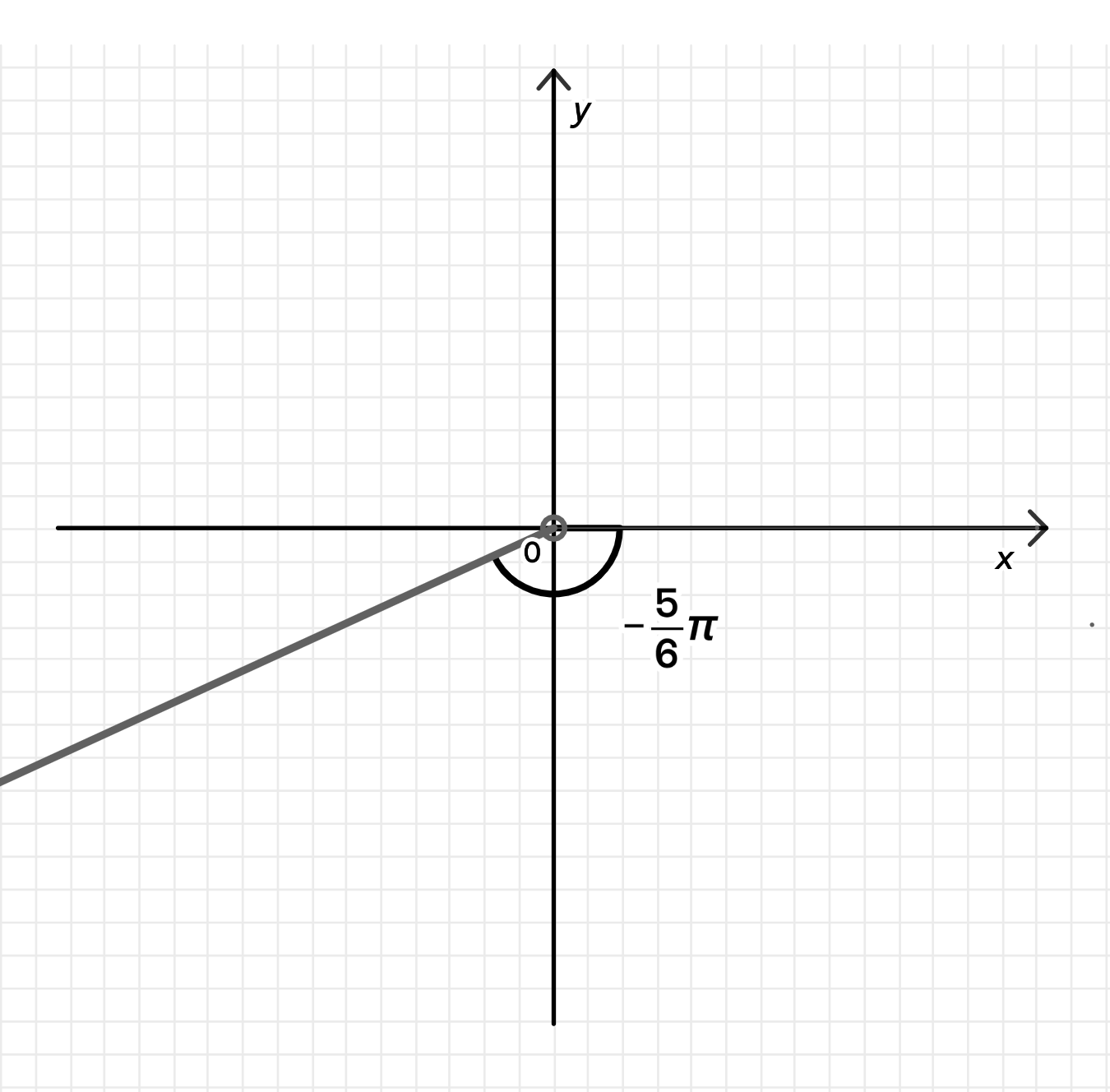
в)
Отсчёт по часовой стрелке на 150°, то есть:
Луч идёт из начала координат под углом 210° (3-й квадрант).
Это — луч, уходящий влево-вниз из начала.
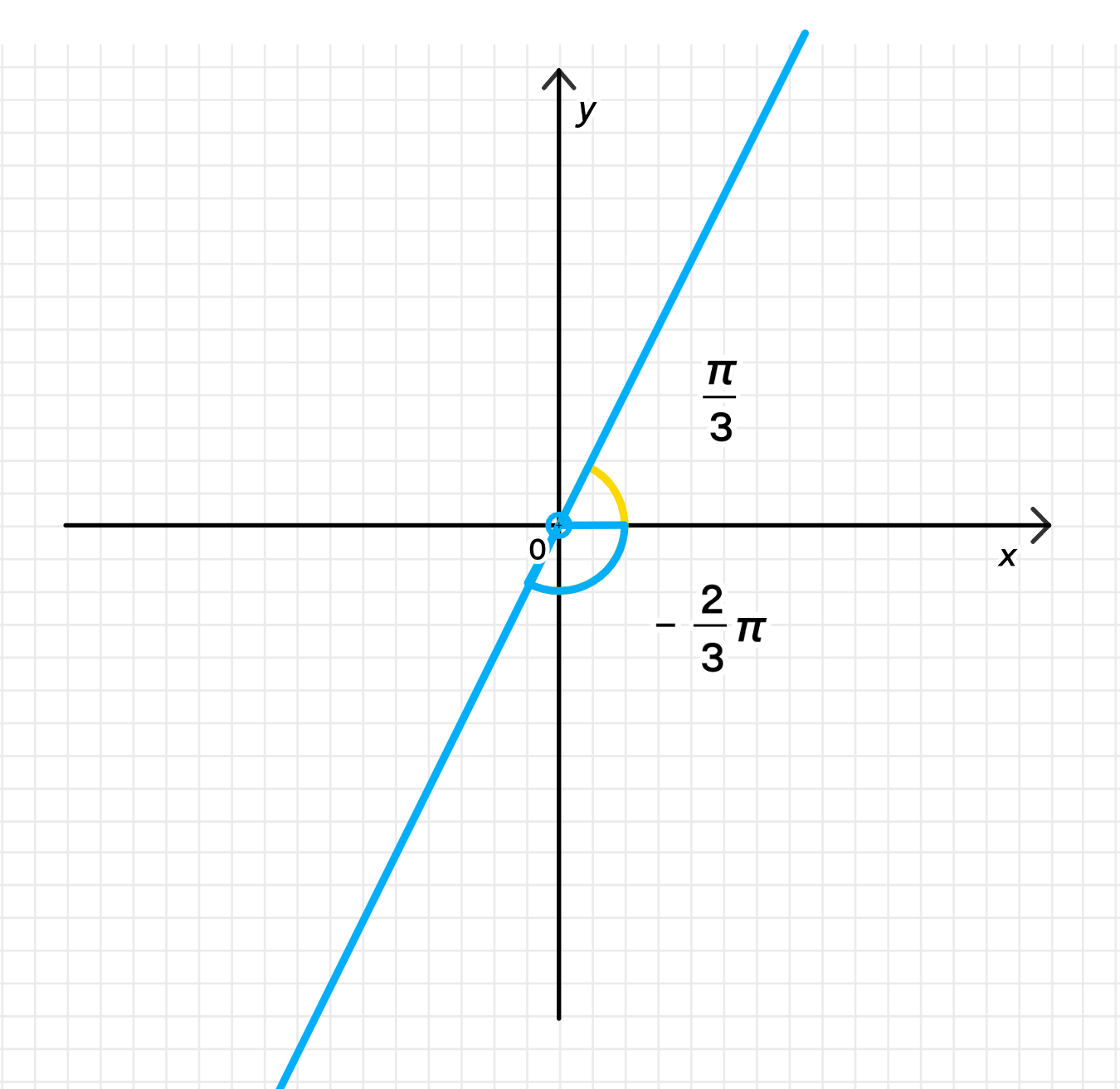
г) или
или
или
Два луча:
— по часовой стрелке 120°, то есть угол 240°.
- Точка будет в 3-м квадранте (влево-вниз, но не вертикально).
Это два луча: один идёт вправо-вверх (60°), другой влево-вниз (240° = -120°).